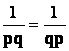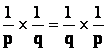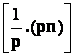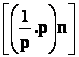COURS

A )   ADDITION :  ( voir cours ….)

1°) Associativité de l’addition. (info plus)

Soient les trois nombres arithmétiques « a » , « b », et « c » ( entiers ou fractions).

On construit les segments  [ A ] ,  [ B ] et  [ C ] ; ………………..et [ U ]   ( voir …@ )

  [ A ] = a . [ U ]

  [ B ]  =  b . [ U ]

[ A ] + [ B ] = ( a + b ) [ U ]

  [ C ]     = c . [ U ]

[ B ] +  [ C ] =  ( b + c ) [ U ]

Et :

[ S  ] =     [ A ] + [ B ]  + [ C ]  =   (  [ A ] + [ B ] )  + [ C ]  =    [ A ] + ( [ B ]  + [ C ]  )

Par suite :

  [ S  ] =    (  [ A ] + [ B ] )  + [ C ]  =  ( a + b ) [ U ]  +  c  . [ U ]     =  [  ( a + b ) + c ] . [ U ]

et :

[ S  ] =    [ A ] + ( [ B ]  + [ C ] )  =  ( a ) [ U ]  +  ( b + c )  . [ U ]     =  [  a +  ( b  + c )  ] . [ U ]

Les opérateurs   « [  ( a + b ) + c ] »       et  « [  a +  ( b  + c )  ] »  agissant sur le même segment « [ U ] » donnent le même segment « [ S ]. Il sont égaux.

Donc :           ( a + b ) + c = a  ( + ( b + c )   ( 1 )

L’addition des nombres arithmétiques est une opération associative.

2°) Commutativité de l’addition.

Soient les deux nombres arithmétiques « a » , « b » ( entiers ou fractions).

On construit les segments :

[ A ] = a . [ U ]

[ B ]  =  b . [ U ]

et

[ S  ] =     [ A ] + [ B ]  ou      [ B ] + [ A ]

On a

[ S  ] =     [ A ] + [ B ]  =  ( a + b ) [ U ]

Et

[ S  ] =     [ B ] + [ A ] =  ( b + a ) [ U ]

donc

«  a + b = b + a »

Et

L’addition des nombres arithmétiques est une opération commutative.

B ) MULTIPLICATION :

1°) Associativité de la multiplication .

Soient les trois nombres arithmétiques « a » , « b », et « c » ( entiers ou fractions).

On construit les segments  [ A ] ,  [ B ] et  [ C ] ; ………………..et [ U ] 

[ A ] = a . [ U ]

[ B ]  =  b . [ A ]  =  b . (  a . [ U ] )  =  ( b a ) [ U ]

[ C ]     = c . [ B ]  =  c  [  ( b .a ) . [ U ] ]  =  [ c ( a b ) ] [ U ]

on a encore :

[ C ]     = c . [ B ]  =   c ( b a )  =   ( c b ) [ A ]  =  ( c b ) ( a [ U ] )  =   [ ( cb ). a  ) ] [ U ]

Les opérateurs [c ( b a ) ]  et  [  ( c b )  a  ]  agissant sur le même segment [ U ] donnent le même segment [ C ]. Ils sont égaux .

Donc

c ( b a )  =  ( c b )  a             ( 2 )

Et :

La multiplication  des nombres arithmétiques est une opération associative.

2°) Commutativité de la multiplication.

Soient les deux nombres arithmétiques « a » , « b »  on démontre que :

«   b a   =  a b »

( 3 )

Autrement dit :

La multiplication des nombres arithmétiques est une opération commutative.

La formule ci-dessus (  3 )  est exacte si « a » et « b » sont deux nombres entiers.
Dans la suite du cours cette formule sera démontrée successivement dans les cas suivants :

« a » et « b » sont des fractions archimédiennes .

« a » est un entier et  « b » est une fraction archimédienne.

« a » et « b » sont des fractions.

C  ) Multiplication de deux  fractions archimédiennes .

1°) Soient les fractions archimédiennes : «  a =   »  et «  b =  »  . On se propose de calculer le produit « b.a »

On a  vu dans le chapitre « opérateur archimédien » :  (    [ A ] ,  [ B ] et  [ C ] ; ………………..et [ U ]   ) 

[ A ] =  [ U ]    ou    [ U ] =   2  [ A ]

[ B ]  =   [ A ]     ou    [ A ]  = 3  [ B ]

[ B ]  =[ U ]

( 4 )

Par suite : [ U ]  = 2   [ A ]

                          =  2 . 3 [ B ]  =   6 [ B ]

D’où :

[ B ]  =  [ U ]

( 5 )

En comparant l’égalité « ( 4 ) » et « ( 5 ) » on voit que :

 = 

2°) De façon plus générale soit  «  a =  »   et  « b =  » .

On a :

[ A ] =   .[ U ]    ou    [ U ] =   p . [ A ]

( 6 )

[ B ]  =   . [ A ]  ou   [ A ]  = q . [ B ]

( 7 )

[ B ]  =. [ U ]

( 8 )

Par suite :

                  [ U ]  = p . [ A ]

                          =  p . ( q . [ B ] )  =  ( p . q )  [ B ]

D’où

[ B ]  =  [ U ]

( 9 )

En comparant  ( 8 )  et (9) on a

 = 

a) Commutativité de la multiplication des fractions archimédiennes.

De même :

 =   

D’où

Et : La multiplication des fractions archimédiennes  est une opération commutative.

b ) Multiplication d’un nombre entier par son inverse.    ( info ++ »opposé et inverse » ++)

Soit un nombre entier « n » et son inverse «  »

On a :

[ A ]  = n . [ U ]       et       [ U ] =  [ A ]

D’où

[ A ]  = n . ( [ A ] )    =   (  n .  )  . [ A ]

Donc

n  x    = 1 

( 10)

On a encore : 

[ U ] =  [ A ]   =   ( n . [ U ]  ) = (   x  n ) . [ U ] 

Donc :

 x n  = 1 

( 11)

c) Commutativité de la multiplication d’une fraction archimédienne et d’un entier.

Soient  les nombres entier    « a =   »  et   « n »

On a : 

[ A ] =   .[ U ]    ou    [ U ] =   p . [ A ]

[ B ]  =  n  . [ A ]  =  (  n x )  .[ U ]

( 12 )

Ou encore

  n   .[ U ]  =  ( n p ) [ A ]  =  (p n ) [ A ] 

( 13 )

Car    « n.p = p.n » ( commutativité de la multiplication des entiers )

Soit alors

[ B ‘  ]  =   (  x n )  .[ U ] =    ( n .[ U ] ) = (p n ) [ A ]

                =    [ A ]

                =    [ A ]

( associativité de la multiplication )

                 =     n   [ A ]

( 14 )

En comparant :  ( 12 ) et   ( 14 )  on voit que [ B ]  = [ B ‘  ]  et donc que : 

(  n x )     =  (  x n )

( 15 )

La multiplication d’une fraction archimédienne et d’un entier est commutative.

Par suite :

  =   n x       =    x n 

21/01/13

CONTROLE:

Combien y a-t-il dans le système  décimal de nombres de 1 chiffre ? de deux chiffres ? de trois chiffres ? de quatre chiffres ?

Quel est le plus grand nombre  de cinq chiffres ? le plus petit ?

Combien faut-il de chiffres pour numéroter un livre de 156 pages ?

EVALUATION: