|
Pour Aide et Formation Individualisée |
CORRIGE TRAVAUX SOMMATIF B. E . P.
9 /15 |
Pour aller
directement aux informations « cours » voir cas
par cas. |
||||||
|
Matière : MATHEMATIQUES |
« TRAVAUX » |
|||||||
|
|
|
|||||||
|
TITRE : |
||||||||
|
|
||||||||
|
OBJECTIFS : Travaux BILAN de fin de formation
en vu d’obtenir une validation de la
formation . |
||||||||
|
|
I ) Pré requis: (pour remédiation ou mise à niveau) |
|
|||||
|
|
Voir le niveau CAP |
|
|||||
|
|
|
|
|||||
|
N° 1 / |
CONSIGNES |
|||||||
|
|
La séquence ne doit pas dépasser 45
minutes. Matériel : le matériel habituel est autorisé :crayon ,
stylo, règle, rapporteur, compas,équerre, calculatrice. Ecrire à l’encre,
dessiner au crayon. (trait fin ,net , précis.) Le devoir est à rendre sur copie blanche. |
|||||||
|
|
|||||
|
|
|
|
|||
|
|
TRAVAUX CONTROLE |
|
|||
|
|
|
|
|||
|
|
Les questions relatives à
« ce qu’il faut retenir » , au
« savoir » se reporter aux cours . |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
TRAVAUX :
EVALUATION |
|
|||
|
|
|||||
|
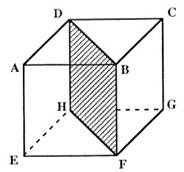
N°1 : voici un cube en
perspective. En réalité , ce cube a une arête de |
|
||||
|
|
|
On le découpe en deux prismes droits
en le coupant selon le plan DBFH . Dans le cadre de droite , Dessiner
, avec ses dimensions réelles , uniquement la face DBFH commune à ces deux
prismes. |
|
||
|
|
|
|
|||
|
|
Réponse on doit dessiner
un rectangle :L = 4 x 1,414 et l
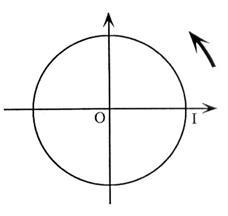
= 4 N°2 sur le cercle trigonométrique
, place les points A , B , C et D tels
que : |
|
|||
|
|
a)
Une mesure de l’angle orienté
b ) Une mesure de l’angle orienté
c) Une mesure de l’angle orienté
d)
Une mesure de l’angle orienté
|
|
|
||
|
|
|
|
|||
|
|
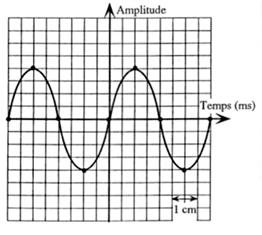
N°3 |
|
|||
|
|
A l’aide d’un microphone relié à
un oscilloscope , on étudie un son. On obtient sur l’écran la courbe
périodique ci - dessous. La base de temps pour l’obtention
de cette image étant réglée sur 0 , 20
ms.cm-1 (ou 0,20 ms/ cm) |
|
|||
|
|
Calculs : 4 x 0,20 = 0,80 Réponse :0,80 ms L’unité est obligatoire. |
|
|
||
|
N°4 |
|
|||||||
|
|
Voici , pour les quatre trimestres
de l’année écoulé , les fréquences du nombre d’autos vendues par un garage (
fréquences données par rapport au
total des ventes de l’année , pour ce garage ) |
|
|
|||||
|
|
Numéro du trimestre. |
1er |
2ème |
3ème |
4ème |
|
||
|
Fréquence des ventes |
0,15 |
0,55 |
0,20 |
0,10 |
||||
|
Fréquences cumulées croissantes |
……0,15…….. |
……0,70….. |
……0,90…… |
……1…….. |
||||
|
|
a) compléter la dernière ligne du
tableau |
|
||||||
|
b) Par rapport aux ventes totales
de 2002, quel est le pourcentage du nombre d’autos vendues du 1er avril au 30 septembre ? réponse :
0,55 + 0,20 = 0,75 |
|
|||||||
|
c) Représenter les fréquences
cumulées croissantes par un diagramme en bâtons ( ou un polygone) |
|
|||||||
|
|
En abscisse on place les
valeurs du caractère « x i »: le trimestre. |
|
||||||
|
|
En ordonnée on met les
fréquences ( f i ) La hauteur de chaque
bâton est proportionnelle à la fréquence de la valeur xi du
caractère. |
|
||||||
|
|
|
|
||||||
|
N°5 : Caroline possède un
ballon sphérique ; En soufflant dans ce ballon, il
parvient à multiplier le diamètre de ce ballon par 2,5 |
|
|||||||
|
|
a)
Par quel nombre le rayon du ballon est -il alors multiplié ? réponse : 2,5 |
|
||||||
|
|
b) par quel nombre l’aire du
ballon est - elle multipliée ? réponse : 6,25 ou ( 2,5 )² |
|
||||||
|
|
b)
par quel nombre le volume du ballon est -il alors multiplié ? réponse :
15,625 ou ( 2,5 ) 3
|
|
||||||
|
|
N°6 |
|
||||||
|
Sans utiliser les touches
« SIN » et
« COS » de la calculatrice . Calculer le sinus de l’angle aigu
dont le cosinus est égal à 0,6. |
|
|||||||
|
|
On utilisera la
relation sin²x + cos ² x = 1 Réponse sin x = 0,8 |
|
||||||
|
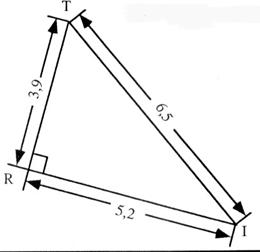
N°7 : Déterminer à un dixième
de degré près la mesure de l’angle « TIR » |
|
|||||||
|
|
Calculs : Démarche soit avec comme
choix le sinus ; le cosinus ou la tangente. Réponse : 36,8° ou
36,9° |
|
|
|||||