TRAVAUX SOMMATIFS	. 7 / 15
INFORMATIONS PEDAGOGIQUES :
	Matière : MATHEMATIQUES	SOS : « CORRIGE »

NIVEAU V :
	TRAVAUX : EVALUATION
??		N°1 : La première année de son ouverture au public , un musée est visité par 250 000 personnes. Durant les années suivantes on enregistre une diminution annuelle de 8 % du nombre de visiteurs.
		a) Quel a été , dans ces conditions, le nombre de visiteurs de la deuxième année ? b) Quel a été le nombre total de visiteurs au cours des deux premières années ? c) Quel a été , dans ces conditions, le nombre de visiteurs de la cinquième année ?
??		N°2
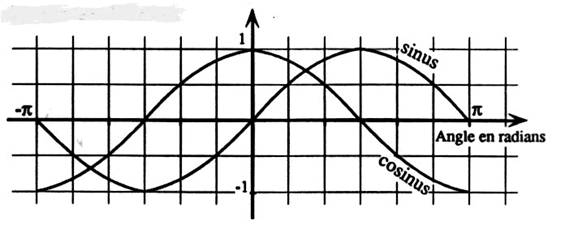
		Les représentations graphiques représentent les variations du sinus et du cosinus d’un angle en radians sur l’intervalle [- p ; p ] On demande : faire apparaître l’axe des abscisses. Faire apparaître sur l’axe des abscisses : a) sin r = 0,5 b) cos s = - 0,5 c) sin t = cos t d) sin u = 1
??		N°3 :
		Calculer la hauteur AH d’un triangle ABC rectangle en A dont les côtés mesurent 3 ; 4 et 5 m
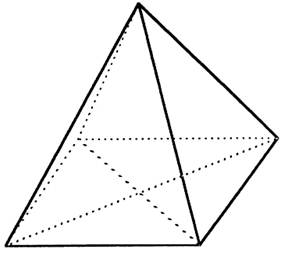
		N°4 : Une pyramide régulière a pour base un carré. Toutes les arêtes de la pyramide ont la même longueur : 14 cm Calculer la hauteur « h » de cette pyramide . Donner une valeur de « h » arrondie au centième prés.
??		N°5 Un plan muni d’un repère , on considère les points : A ( 3 ; 3 ) ; B ( -2 ; 4 ) ; C ( -1 ; -3) Calculer les coordonnées du vecteur « AB » et du vecteur « BC »
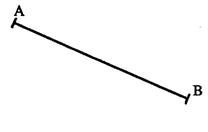
??		N° 6 Sans utiliser la graduation de la règle , construire le points M du segment [A B ] tel que  ; on laissera les traits de construction.
		Réponse :
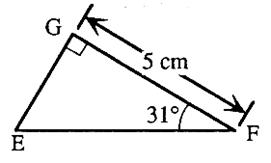
??		N°7 ( attention : le dessin ne respecte pas les mesures)
		En utilisant les données potées sur le dessin ; DETERTMINER la mesure du côté [ EF ] ; au millimètre prés.
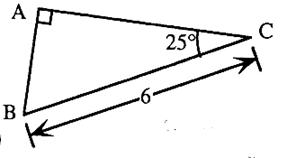
??		N°8 ( attention : le dessin ne respecte pas les mesures)
		Sachant que cos 25° = 0,906307 Calculer une valeur approchée au centième prés de AC .

Fin des travaux 7 / 15