warmaths Pour Aide et Formation Individualisée			TRAVAUX SOMMATIF B. E . P. 7 / 15		Pour aller directement aux informations « cours » voir cas par cas.
INFORMATIONS PEDAGOGIQUES :
DOSSIER N° 6 / 15			Matière : MATHEMATIQUES		« TRAVAUX »
TITRE : CORRIGE devoir test ou bilan de niveau V
Classe : B. E . P. NIVEAU : niveau V				OBJECTIFS : Travaux BILAN de fin de formation en vu d’obtenir une validation de la formation .
	I ) Pré requis: (pour remédiation ou mise à niveau)
	Voir le niveau CAP
N° 1 /		CONSIGNES
		La séquence ne doit pas dépasser 45 minutes. Matériel : le matériel habituel est autorisé :crayon , stylo, règle, rapporteur, compas,équerre, calculatrice. Ecrire à l’encre, dessiner au crayon. (trait fin ,net , précis.) Le devoir est à rendre sur copie blanche.

	TRAVAUX CONTROLE
	Les questions relatives à « ce qu’il faut retenir » , au « savoir » se reporter aux cours .
	TRAVAUX : EVALUATION
??		N°1 : La première année de son ouverture au public , un musée est visité par 250 000 personnes. Durant les années suivantes on enregistre une diminution annuelle de 8 % du nombre de visiteurs.
		a) Quel a été , dans ces conditions, le nombre de visiteurs de la deuxième année ? 230 000 b) Quel a été le nombre total de visiteurs au cours des deux premières années ? 480 000 Quel a été , dans ces conditions, le nombre de visiteurs de la cinquième année ? 179 098 visiteurs ou autre approximation Obtenu par calcul directe avec la formule ou calcul par années successives.
		N°2
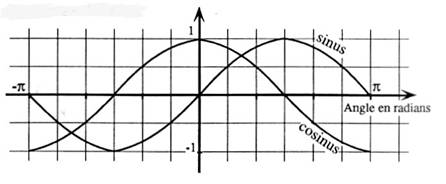
		Les représentations graphiques représentent les variations du sinus et du cosinus d’un angle en radians sur l’intervalle [- p ; p ] On demande : faire apparaître l’axe des abscisses. Faire apparaître sur l’axe des abscisses : a) sin r = 0,5 réponses : p / 6 et 5p / 6 b) cos s = - 0,5 réponses : - p / 6 et 2p / 3 (ou 4 p / 6 ) c) sin t = cos t réponses : - 3 p / 4 et p / 4 d) sin u = 1 réponses : p / 2
		N°3 :
		Calculer la hauteur AH d’un triangle ABC rectangle en A dont les côtés mesurent 3 ; 4 et 5 m
		Utiliser la formule : AH x BC = AB x AC ou Utilisation de la trigonomètrie. Réponse : 2,4 m
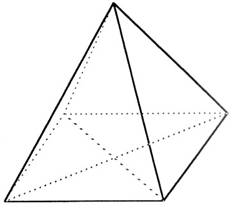
		N°4 : Une pyramide régulière a pour base un carré. Toutes les arêtes de la pyramide ont la même longueur : 14 cm Calculer la hauteur « h » de cette pyramide . Donner une valeur de « h » arrondie au centième prés.
		Réponse : on recherche un triangle utile (dont on connaît 2 valeurs sur 3. Ensuite énoncer le théorème ( ou la relation ou la propriété) de Pythagore. Réponse 9,89 cm ( ou 9,90 ) ou toute valeur approchée compatible avec des calculs exacts.
??		N°5 Un plan muni d’un repère , on considère les points A ( 3 ; 3 ) ; B ( -2 ; 4 ) ; C ( -1 ; -3) Calculer les coordonnées du vecteur « AB » et du vecteur « BC »
		Réponse : le vecteur AB : ( - 4 ; 1 ) et le vecteur BC : ( 1 ; - 7 )
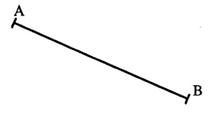
??		N° 6 Sans utiliser la graduation de la règle , construire le points M du segment [A B ] tel que  ; on laissera les traits de construction.
		Réponse :
		Réponse : s’appuyer sur la propriété de Thalès.
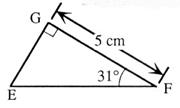
??		N°7 ( attention : le dessin ne respecte pas les mesures)
		En utilisant les données potées sur le dessin ; DETERTMINER la mesure du côté [ EF ] ; au millimètre prés.
		Réponse : on utilise le cosinus de l’angle F ; 5,8 cm ou 58 mm
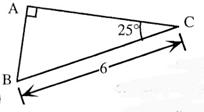
??		N°8 ( attention : le dessin ne respecte pas les mesures)
		Sachant que cos 25° = 0,906307 Calculer une valeur approchée au centième prés de AC .
		Réponse : 5,44 ou 5,43