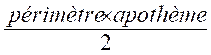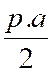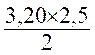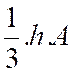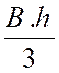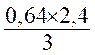Pré requis:

Les polyèdres

ENVIRONNEMENT du dossier:

Index

Objectif précédent : la pyramide

Objectif suivant :le tronc de pyramide

Liste des cours en géométrie dans l’espace.

DOSSIER : LES  PYRAMIDES.

1°)  Les pyramides régulières. ( définition (1) et (2) ; rappels sur les calculs : d’aire et de volume )
2°)  Les modèles de  pyramides régulières et  irrégulières..
3°) le développement d’une pyramide.
TEST	COURS	Devoir  Contrôle	Devoir évaluation	Interdisciplinarité		Corrigé Contrôle	Corrigé évaluation

 

COURS

 

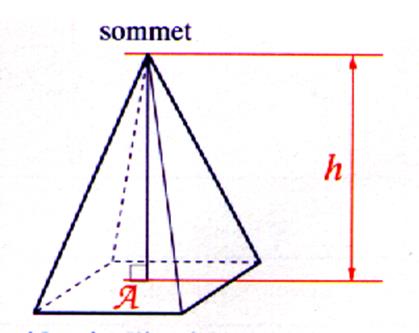
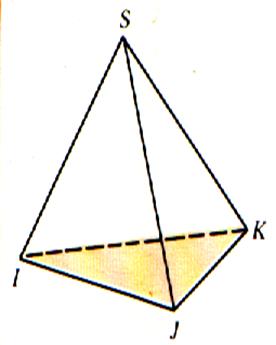
Définition 1 :  Une pyramide est un solide limité qui a pour base un polygone quelconque et pour faces latérales des triangles ayant un sommet commun.

 

1°)    Les   pyramides régulières :

 

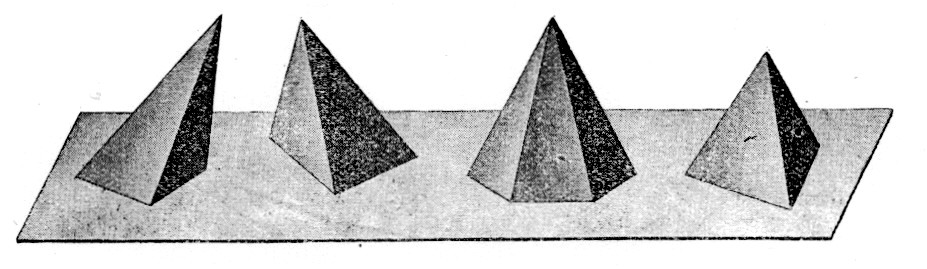
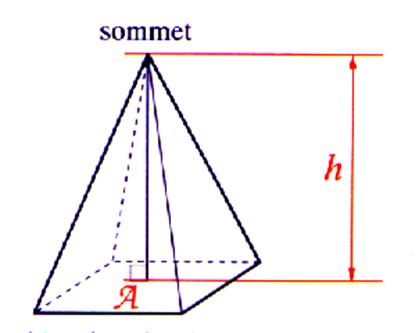
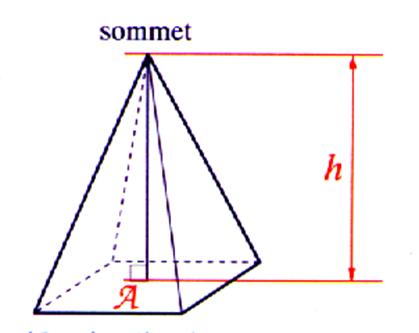
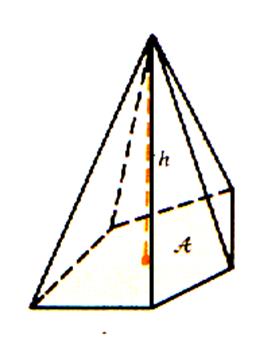
Une pyramide est régulière lorsque  sa base est un polygone régulier et que sa hauteur « tombe » au centre du polygone .

Les arêtes latérales obliques s’écartent également du pied de la hauteur perpendiculaire ,elles sont égales en longueurs ; les facettes latérales  sont donc des triangles isocèles.

Exemple :la grande Pyramide d’ Egypte est une pyramide régulière à base carrée ; les facettes latérales sont des triangles isocèles presque équilatéraux.

 

CALCULS :

 

I )  SURFACE LATERALE :

La surface latérale d’une pyramide régulière est égale  à la moitié du produit  du périmètre de la base par l’apothème de la pyramide .

Ce qui se traduit :             Surf. Latérale =

 

Ou                             A = 

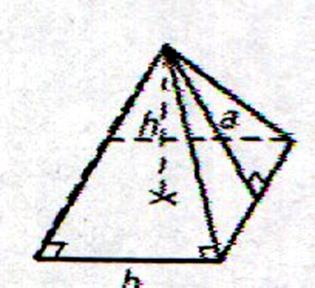
L’apothème « a » est une droite issue du sommet de la pyramide  et sommet du triangle isocèle  et joignant le côté opposé  du triangle (face latérale) en son milieu . Il y a autant d’apothème que de faces latérales. Cette apothème est a la fois médiane médiatrice bissectrice et hauteur.  .

Application :

Une pyramide à pour base un carré de  0,80 m de côté ; son apothème égale 2,50 m. Trouver :

1°) le périmètre de base .

2° ) sa surface latérale.

 

Résolution :

1°) le périmètre de base .= 0,80 m  4 = 3,20 m

2° ) sa surface latérale.=  = 4 m²             

 

COMPLEMENT de CALCULS :

Périmètre de base	voir cas pas cas : SOS info
Aire de base	voir cas pas cas : SOS info

 

 

 

II ) SURFACE TOTALE :

             la surface totale est la somme de la surface latérale et de la surface de base .

 

Application :

Une pyramide à pour base un carré de  0,80 m de côté ; son apothème égale 2,50 m. Trouver : sa surface totale .

 

Résolution :

 Surface de base :  A = 0,80m0,80m =  0,64 m²

Surface latérale.=  = 4 m²

Surface totale . 4 m² + 0,80m0,80m =4 m² +  0,64 m²  = 4,64 m²

 

 

III ) VOLUME

                      Un prisme triangulaire peut – être décomposé en 3 pyramides équivalentes .

                       Le volume d’une pyramide est ainsi égal au tiers du produit de la surface de base par sa hauteur.

 

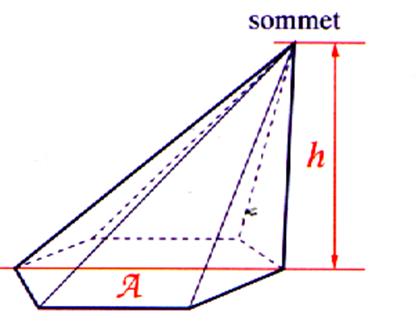
Définition 2 :  Une pyramide est un solide limité par un angle polyédral et une section plane s’appuyant sur toutes les arêtes.
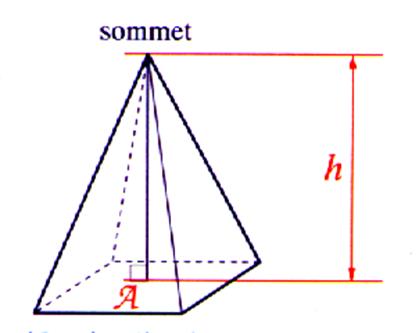
Volume de la pyramide à base carrée : V = « h » est la hauteur et « A » l’aire de la base ; ou :   V =   « B » étant l’aire de base
Volume de la pyramide à base polygonale :   V =   « h » est la hauteur et « A » l’aire de la base

 

Application : Une pyramide à pour base un carré de  0,80 m de côté ; sa hauteur égale 2,40 m. Trouver son volume  .

 

Résolution :

Surface de base :  A = 0,80m0,80m =  0,64 m²

Volume :=  =0,512 m³

 

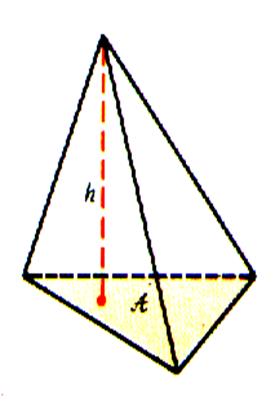
2°)   Les   modèles de pyramides régulières et irrégulières.    voir cas par cas :  SOS INFO
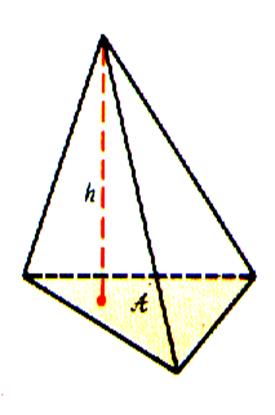
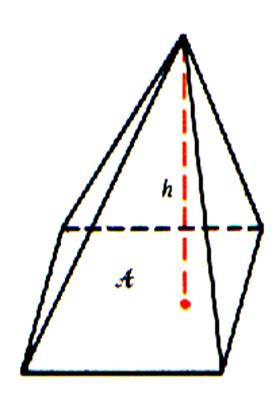
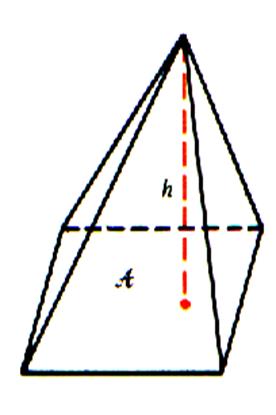
Régulière ; quadrangulaire		Irrégulière ; triangulaire	Irrégulière, quadrangulaire
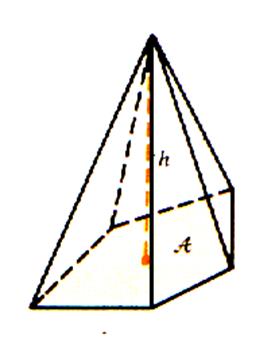
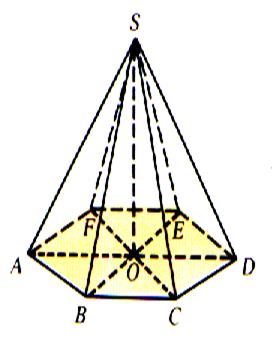
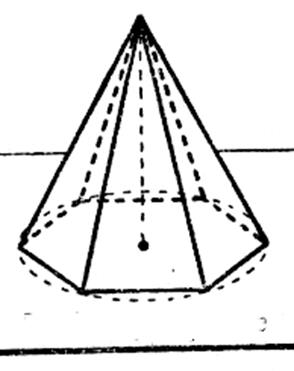
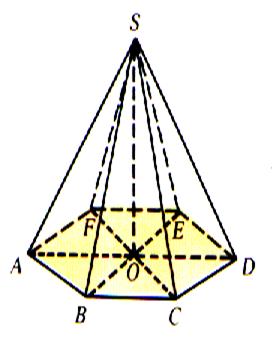
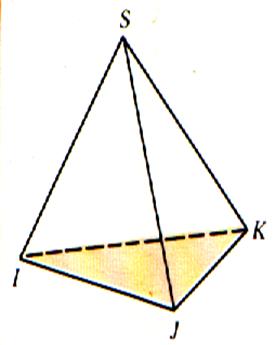
Régulière ; pentagonale		Régulière ; hexagonale	Irrégulière ; triangulaire
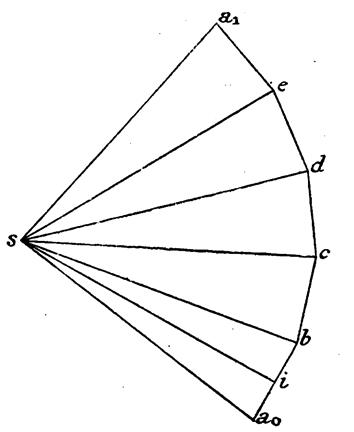
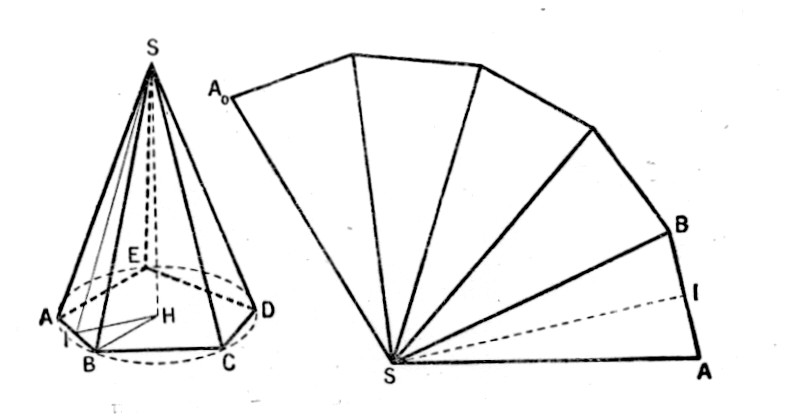
3°)  Le développement d’une pyramide :

 

 

TRAVAUX AUTO FORMATIFS.

 

CONTROLE :

 

1°) Donner la formule permettant de calculer la surface latérale d’une pyramide :

 

2°) Donner la formule permettant de calculer la surface de base d’une pyramide :

 

3°) Donner la formule permettant de calculer la surface totale d’une pyramide

 

4°) Donner la formule permettant de calculer le volume d’une pyramide.

 

 

 

EVALUATION

 

Exercices :

A ) Une pyramide à pour base un carré de  0,80 m de côté ; son apothème égale 2,50 m. Trouver :

1°) le périmètre de base .

2° ) sa surface latérale.

 

B ) Une pyramide à pour base un carré de  0,80 m de côté ; son apothème égale 2,50 m. Trouver : sa surface totale .

 

C ) Une pyramide à pour base un carré de  0,80 m de côté ; sa hauteur égale 2,40 m. Trouver son volume  .

 

D)

Calculer : - l’aire de la surface latérale - l’aire totale - le volume de la pyramide régulière avec les données suivantes : a = b = h =

 

PROBLEMES :

 

1°) Un toit en forme de pyramide a pour base un carré de 22,40 m de pourtour . La hauteur des triangles latéraux égale 8,50 m . Que coûtera la couverture de ce toit , à 1250 €.

 

2° ) Une pyramide a pour base un hexagone de 0,70 m de côté . La hauteur des triangles  latéraux égale 1,80 m . Calculer la surface latérale de la pyramide .

 

3° )La grande pyramide d’Egypte a 142 m de haut . Sa base est un carré de 233m de côté. Quel est son volume ?

 

4 ) )Une petite pyramide de bronze est plongée dans un vase plein d’eau. Quel est le poids qu’elle fait sortir , sachant quelle mesure 8 cm de haut et que sa base est un carré de 0,07 m de côté ? 

 

5°) Une pierre a une forme pyramidale de O,45 m de hauteur et dont la base est un hexagone de 0 ,10 m de côté et O,O86 m d’apothème ;Quel est le poids de cette pyramide , la densité de la pierre étant de 2,5 ?

 

6°) Une pyramide a 12,5 dm³ de volume et 625 cm² de base . Quelle est sa hauteur ?

 

7°) Une pyramide a 171,5 cm³ de volume et 0,42 m de hauteur ; sa base est un carré . Quel en est le périmètre ? 

 

 

8° )  niveau +++++ : 

             Parmi ces pyramides : identifier les « régulières »  et les « irrégulière » ; donner leur un nom particulier ; établir la formule permettant de calculer le volume de la pyramide .

 

Modèles de pyramides : voir cas par cas :  SOS INFO
Régulière ; quadrangulaire	Irrégulière ; triangulaire	Irrégulière, quadrangulaire
Régulière ; pentagonale	Régulière ; hexagonale	Irrégulière ; triangulaire

 

 

 

 

 

 

 

 

INTERDISCIPLINARITE