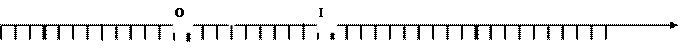|
Niveau VI et
V |
Pré requis
|
|
|
|
|
|
|
|
|
|
|
|
2°)droite graduée . |
1°)Repérage d’un point dans un repère cartésien ( 4 quadrants
) |
Tableau : Classe 6éme |
|
|
DOSSIER : ABSCISSE d'un point (sur un axe gradué
avec des nombres entiers relatifs) |
|
|||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
1°)
Définition : |
|
|||||
|
|
2°)
Abscisse d’un point : |
|
|||||
|
|
3°)
Mesure algébrique : la mesure algébrique de l'origine O à un
point considéré : |
|
|||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
||||
|
|
|
|
|
|
|
||
Définition :
Un axe est une droite graduée munie d’un repère ( O,
I ) ; O est l’origine du repère , et I est le point d’abscisse 1 .
Pour graduer une droite :
-
il faut orienter cette droite (
flèche )
-
il faut choisir un point d'origine "O"
-
choisir un longueur unité "u"
( exemple :
-
Graduer la demi-droite positive , les graduations
sont numérotées avec les décimaux positifs.
-
Graduer la demi-droite négative , les graduations
sont numérotées avec les décimaux négatifs.
Exécution de la graduation :
La
graduation ( petit trait ) s'effectue soit avec un compas ou une règle
graduée , ensuite on numérote : +1 ; +2 ;
+3 ; …. Pour les négatifs -1 ; -2 ; -3 ;…..
-
A la
règle graduée le segment OI mesure
-
au
compas : On prend un écartement au
compas égal à la longueur du segment [0I] ; on place le point O ( 0) et le I (+1) ,on reporte ce segment autant de fois
que cela est nécessaire.

A chaque point "M" , ou "A" ou "B" de l’axe
correspond un et un seul nombre relatif
noté xM , ou xA ou xB .
Ce
nombre est appelé
" abscisse" de M ou de A ou de B.
Ici le point
A à pour abscisse ( + 2,8)
Commentaire
:
Chaque
graduation d'unité OI = u = 1 ; peut
se subdiviser en 10 parties égales (et
ainsi de suite ; chaque subdivision peut encore se diviser en 10 parties
égales.)
Chaque unité de graduation diviser en dix parties égales représente :.
- les dixièmes d’unités.
Chaque graduation
de " 1" unité peut se subdiviser en 10 parties égales.(nous obtenons les
dixièmes d’unités)
Ces 10 parties égales peuvent se subdiviser aussi
en 10 parties égales . .(nous obtenons les dixièmes d’unités)
Il est
possible de diviser chaque dixième
d'unité en 10 ce sont des
les centièmes d’unités.
et ainsi de
suite chaque subdivision peut encore se diviser en 10 parties égales. .(nous obtenons les millièmes d’unités)
CAS courant :
On utilise le papier
millimétré
les
graduations sont de
|
Abscisse d’un point : |
Définition
:
L’abscisse
d’un point sur un axe est « une
valeur algébrique » ( nombre
décimal relatif ) correspondant à la
graduation de ce point .
ABSCISSE d’un point sur une
droite :
Lorsque
nous avons comme repère une
droite graduée ; nous l ’ appelons couramment : droite des « x » ou « droite,
ou ligne des
abscisses » ;
Chaque position d'un point est marqué sur une droite et est nommé par une lettre majuscule ;
Dans
un énoncé , ou dans la réponse d'un devoir
, la lettre majuscule est associée à une valeur numérique
.(positive ou négative)
Exemples : A (+2)
; B (-1) ; C (+4)
Commentaire : La valeur absolue du nombre relatif nous informe sur le nombre de graduation
qui se sépare le point considéré et l’origine des
graduations (point O) .
Exemples :
A(+2) :
la valeur absolue de + 2 est
2 ; le point A se trouve à
2 graduations de l’origine ( point O)
B (-1) :
la valeur absolue de -1 est 1 ; le point B se trouve à 1 graduation de l’origine ( point O)
C (+4) :
la valeur absolue de +4 est 4; le
point C se trouve à 4 graduations de
l’origine ( point O)
représentation
graphique :
A
C
B

Mesure algébrique de l'origine O
à un
point considéré :
Lorsque l'on connaît
l'abscisse d'un point on en "déduit" la mesure algébrique de l'origine O au le point considéré .
"déduit" cela signifie qu'il n'y a pas de
calcul , c'est simplement une mise en écriture d'une réponse .
La mesure algébrique d ‘ un bipoint est un nombre relatif , l’analyse du nombre
permet de connaître la norme (pour
la valeur absolue) et le sens ( pour le signe + ou - )
d’un vecteur sur un axe ; ou de
sa composante sur l ’ axe « x’ x » ou « y’
y » .
Le nombre relatif n ‘ a pas d’unité de mesure .
Exemple :
Le point A à
pour abscisse (+2) ; la mesure algébrique
de O à A est 2 ; on la notera :
![]() = 2
= 2
Le point B à
pour abscisse ( - 1 ) ; la mesure algébrique de O à B est
-1 ; on la notera : ![]() = - 1
= - 1
Le point O a pour
abscisse 0 : ![]() = 0
= 0
Activités :
N°1 : on donne les coordonnée des points M ( 0,5) ; N ( -2) et P ( 2,25) , les placer
sur la droite graduée :
|
|
N°2 : On
donne des points sur une
droite A , B , C et un segment unitaire (O,I);
Graduer la droite et donner les abscisses de ces
points
|
|
Solution de
l'activité 1 :on a placé les points
N;M;P
|
|
Solution de l'activité 2 :
On numérote les graduations ; et l'on relève les
valeurs :A (+1,5) ; B ( -1) ; C (+3)
|
|
TRAVAUX AUTO
– FORMATIFS.
1°) Donner la
définition d’un axe :
2°)Qu’appelle-t-on abscisse d’un point ?
EVALUATION
Série 1 :
A )
Traduire XA : lire
b ) Traduire A (+3,2) lire
c) Traduire : ![]()
Série 2 :
N°1 :
on donne les coordonnée des points M ( 0,5)
; N ( -2) et P ( 2,25) , les placer sur la droite graduée :
|
|
N°2 :
On donne
des points sur une droite A , B ,
C et un segment unitaire (O,I);
Graduer
la droite et donner les abscisses de ces points
|
|
Série 3 :
1°)construire un axe (graduée pour placer des nombres
décimaux relatifs (les bornes (maxi)
sont –4 et +6 ) .
2°) Placer sur l’axe précédemment
tracer les points:
A(-3, 7 ) ; B(- 0,5 ) ; C (+0,2 ) ; D (1,1) ; E (+2,8)
sachant que la longueur [O , I
] est égal à
Série
4 :
Construire
une droite graduée ( x' x ) , orientée de gauche vers la droite, l'unité est le
centimètre .
Placer
les points A , B , C , D , E d'abscisses respectives 0,5 ; -4,5 ; 6,3 ;
2,7 ; -2,1 .
Série
5 :Compléter la
graduation de la droite ci -
dessous . Placer les points A ; B , C ,
D, tels que :
![]() = - 4 ;
= - 4 ; ![]() = 3 ;
= 3 ; ![]() = -2,5 ;
= -2,5 ; ![]() = 6,3
= 6,3
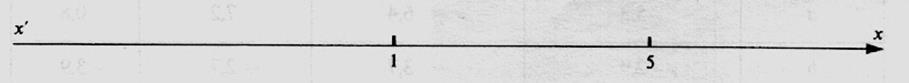
|
Série 6 : |
|
|
TC2 |
E |
T |
C |
|
Repérage sur une droite : Soit
une droite munie d’une graduation de repère (O,I) |
|
|
|
|
|
1°) exercice soit les points sur la droite : |
|
|
|
Déterminer les abscisses de ces points : O (___ ) ; I (__) ;A
(__) ; B (__ ) ;C ( __) ;D ( __) ; E (__) ; F (__) |
|
2°) après avoir gradué la droite ; Placer les points : M (+2) ; N
(-1,4) ;P ( +0,6) ; Q ( +2,8) ; R ( -2,4) |
|
|