Pré requis: (minimaux)
|
Repères cartésiens |
|
|
Calcul numérique du type |
|
|
Equation du premier degré à une
inconnue |
|
ENVIRONNEMENT du dossier:
|
Objectif précédent 1°) la |
Tableau |
Les modèles de représentation mathématique
Travaux:
|
TEST |
COURS |
Devoir Contrôle |
Devoir évaluation |
Interdisciplinarité |
|
Corrigé Contrôle |
Corrigé évaluation |
Ce
cours vous présente les 4 MODELES MATHEMATIQUES de la représentation de la fonction
Affine
EQUATION :
Il faut Connaître
la notation x a ax + b; pour
une valeur numérique de « a » et
« b » fixée.
cet objectif traite des généralités sur la fonction
dite « affine » appliquée à l’équation :
y = ax + b
Exemples de fonction : y = 2x –1 ; y =
-x + 3 ; y = m x + p
|
Si "a" est une fraction ou écriture fractionnaire voir
le cours pour le calcul avec "x" |
Une
fonction affine peut s’identifier à
partir de quatre modes de représentation :
A) EquationLéquation
de la forme : y = ax +b)
B) Graphe
(très difficile)
C) Tableau
de variation (très difficile )
D) Représentation
graphique. (droite ne passant par "0" )
EXEMPLE appliqué
à une équation
y = 
x + 2
I)
EQUATION :
soit y = 
x+2
Notation
mathématique de la fonction linéaire :
f :
x
x+2
traduction en langage littérale :
« fonction » où « x » () "a pour
image" « » fois « x » plus deux.
Ce que l'on peut dire de « x + 2 » :
|
« |
|
"2" est un nombre appelé
"constante" il remplace la
lettre "b" |
|
« |
|
« x » est la variable de la fonction. |
On
dira :
Que la fonction affine de coefficient « » fait correspondre à chaque valeur de la variable
« x » le nombre « x + 2 ».
L’équation représentant de la fonction affine est une équation du premier degré à deux
inconnues de la forme y = x+2
REMARQUE
:
bien entendu dans l'
équation : y = ax + b il faut que
"a" soit différent de zéro ; au cas ou nous aurions une autre équation qui sera de la forme :
y = 0x + b
soit y = + b
Voir l'étude du cas particulier :
|
|
II )
Graphe de la fonction affine (construit
à partir d’une équation)
Graphe d' une fonction affine est de la forme :
G = {( x1 ; ax1+b) ;
(x2 ;ax2+b) ; ......... }
Application :
Le graphe
est un ensemble de couples de nombres (ou suite);du type : ( x ; ax+b)
le premier nombre est
attribué à « x » (valeur choisie)
le deuxième nombre est obtenu ,
après avoir remplacé "x" par la valeur précédemment choisie et avoir
fait le calcul « ax + b».
Exemple
: On donne y = x+2
On remarque que « a » vaut et "b" vaut
2 ;
le couple "type" du
graphe aura la forme et sera noté :
( x ; x+2)
modèle
mathématique :
ce qui
donnera pour l' équation : y = x+2 ; le graphe
sera de la forme
G = {( x1 ;
x1+b) ; (x2 ; x2+b ) ; ......... }
Si l'on choisi des valeurs pour "x" on peut alors construire des couples de nombres
et ainsi obtenir un graphe de cette
"fonction"
Construction d’un couple de nombres (à
partir d’une équation) :
Si l’on donne une valeur à
« x » (exemple : 9 )
on
obtient un autre nombre en utilisant
l’équation y = x+2 ;
(y
= 
9+2 ; y =
(18 :3 ) +2 ; y = 6 +2
; y = 8)
c'est
ainsi que nous obtenons le premier
couple de nombres du graphe de la fonction « x +2 » :
(9 ; 8)
On remarque que l’on peut citer un couple particulier de la forme: (0 ;b ) ; on a donné la valeur "0" à "x"
Conclusion :
le graphe représentant l ’ équation y = x + 2
est G = {( 0 ; 2) ; (9 ; 8 )}
|
Représentation
graphique de la fonction affine: |
|
Construction
dans un repère cartésien:
I) à partir d’un graphe :
soit le graphe obtenu
précédemment G = {( 0 ; 2) ; (9 ; 8 )}
,ces deux
couples de nombres permettent de tracer la représentation graphique de la
fonction .
Procédure : reporter les deux points ; A ( 0 ; 0) ;
B (9 ; 8 )
remarque : Dans un repère cartésien , pour le
couple (x1 ; x1+2)
à x1 on associe l’abscisse « x » appartenant à
l'axe des "x"
à « x1+2 » on associe l’ordonnée « y1 » ;
appartenant à l'axe des "y"
Si on analyse ce graphe : G = {(
0 ; 2) ; (9 ; 8 ) }
On reconnaît que la droite passe par
le point y = 2 pour x = zéro ,
on
peut dire le second couple de nombres (9 ; 8 ) est de la forme (x ; ax+b ) ; à démontrer ce qui n'est pas évidence au prime abord .
III)
TABLEAU de variation (regroupant les couples ( x ; x+2) )
Présentation du tableau numérique:
|
|
|
A |
B |
C |
O |
D |
E |
|
|
|
|
x |
-3 |
-2 |
-1 |
0 |
+1 |
+3 |
+6 |
|
|
|
y |
0 |
1,25 |
4/3 |
2 |
+8/3 |
+4 |
+6 |
|
Les coordonnées du point A peuvent se noter
verticalement :
A xA au lieu de A (xA ,yA)
yA
A
chaque point (A ;B ;.....) est associé les deux nombres qui serviront
de coordonnées dans la représentation graphique.
Pour faire la représentation graphique dans un
repère cartésien on prend dans le
tableau ,au minimum, deux points ( A (-3 ;-0); O (0; 2) ;
on trace la droite passant par ces ceux points ; on choisi un troisième point et l'on vérifie si il est bien sur la droite tracée
précédemment :
E(+3 ;+4).......)
IV ) Représentation graphique de l’équation : y = x + 2
La
représentation graphique d ’ une équation passe par la recherche de plusieurs couples de nombres ,utilisés
comme coordonnées .
Deux points suffissent pour tracer la
droite ;plus un troisième qui servira de moyen de vérification (il doit se
trouver sur cette droite )
la représentation graphique de la fonction
linéaire est une droite (noté xx +2) , où l’ensemble des points A, B ,C ,D,
........ ont pour coordonnés les couples de nombres (x ; x+2 )
Caractéristique de cette représentation
graphique :
n
c’est une droite (D)
n
cette droite passe par
l’origine « A » d ’ abscisse (0) et d’ordonnée (2) , noté (0 ;2)
n
elle possède un point
caractéristique ; à d’abscisse
valeur « 1 » correspond la
valeur de « » ; noté P :(1 ; 
)
« » s’appelle coefficient directeur de la droite , c’est un nombre
relatif :, il est « positif »
,dans la représentation graphique la droite monte de la gauche vers la
droite ,on dira que la fonction est « croissante ».,
4
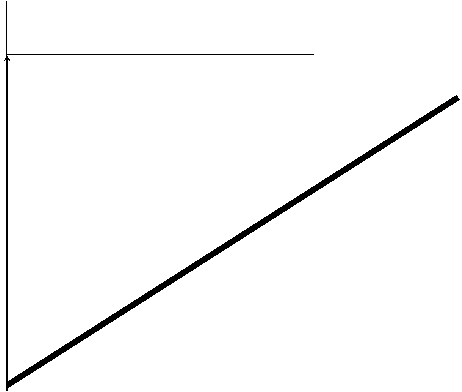
y
2
A
|
1
+
x
1 2 3
Dans la fonction linéaire nous
avions vus :
Le coefficient directeur
« » est un nombre relatif .
« » peut s’appeler :
n
Coefficient de proportionnalité (dans le tableau)
n
Coefficient directeur de la droite de la fonction linéaire.
n
Coefficient directeur de la droit d’équation y = x ; dans la représentation graphique
Dans un repère cartésien orthogonal ; dans la
représentation graphique de l’équation y = x ; «» est appelé « pente de la droite », la
« pente » étant appelée aussi
« tangente » ;
la pente est obtenu par le rapport de « y » sur « x ».
Voir les relations trigonométriques dans un triangle rectangle
|
Le coefficient directeur de la droite est un
nombre : « positif ou
négatif » . |
CALCUL de la PENTE
et TANGENTE
A
propos de "a" dans y = ax+b : «
a » est aussi appelé « pente »
ou « tangente »
de la droite. ; à condition d’être dans un repère cartésien orthonormal
Ainsi dans l’équation y = x + 2
«» est aussi appelé
« pente » ou « tangente » de la
droite.
voir relations trigonométriques dans A
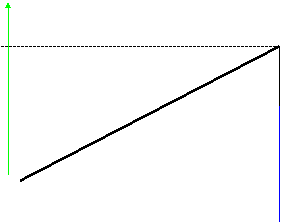
yA
0
·
xA A’
la pente
est égale au rapport de la longueur « xA » sur la
longueur « yA »
;
on dit
aussi égale au rapport de la longueur du segment AA’ sur la longueur du segment OA’ ;
on dit aussi
au rapport du coté opposé a l’angle (AA’ ) sur le coté adjacent
(OA’)
on dit
aussi égale à l’abscisse du point A sur
l’ordonnée du point A
Application :voir classeur (à sacnériser)
TRAVAUX AUTO FORMATIFS.
1.
Donnez le modèle
mathématique de l’équation représentant
la fonction affine
2.
Que peut-on
représenter avec une équation représentant la fonction affine ?
3.
Soit la notation « ax » , comment nomme - t - on
les facteurs ?
4.
Donnez la forme des
couples qui forment eux mêmes le graphe
de la fonction affine
5.
Donner les deux couples
caractéristiques qui forment le graphe
de la fonction affine
6.
Représenter le tableau de
variation de la fonction affine; précisez ce qu’il « contient ».
7.
Définissez « la
représentation graphique » de la fonction affine;
·
précisez ,en citant les
caractéristiques principales ; placer les dans un repère cartésien.
8 Comment reconnaît - on
une fonction dite
« affine » ?
Rappels :
Qu’appelle -t - on
« tableau de variation »
?
Que désigne le mot « variable » ?
I
) Calculer : Savoir trouver la valeur de
« y » . On donne une valeur à
«a ; x ; b » dans les cas suivants :
|
(remplir
le tableau suivant) |
|
|
|
|
|
a = |
x = |
b
= |
y = ax + b |
Résultat y = |
|
+3 |
+2 |
+2 |
|
|
|
-
3 |
+2 |
+2 |
|
|
|
0,5 |
-2 |
+2 |
|
|
|
-1,5 |
-2 |
+3 |
|
|
|
1 /
3 |
1 |
-0,5 |
|
|
|
-
2 / 3 |
3 |
1,5 |
|
|
II ) Compléter
le tableau suivant :
On donne des valeurs , les remplacer dans l'égalité , faire le
calcul :
|
a = |
x = |
b = |
y = |
Mettre sous la forme y = ax + b |
|
|
+2 |
+2 |
+8 |
|
|
-
3 |
|
+2 |
+4 |
|
|
0,5 |
-2 |
|
1 |
|
|
-1,5 |
|
+3 |
+3 |
|
|
1 /
3 |
1 |
-0,5 |
|
|
|
-
2 / 3 |
|
1,5 |
-0,5 |
|
III
) Soit
les fonctions :
|
y1
= 2x +1 |
y2
= - 2x +0,5 |
y3
= 3x -1 |
1°) Dans un repère cartésien orthonormé ; Faire la
représentation graphique de chaque fonction .
|
A l' équation y1 = 2x +1 |
On associe la droite D1 (lire :droite indice 1) |
|
A l' équation y2 = - 2x +0,5 |
On associe la droite D2 (lire :droite
indice 2) |
|
A l' équation y3 = 3x -1 |
On associe la droite D3 (lire :droite indice 3) |
2°) En
étudiant le graphique , donner les coordonnées du point d’intersection des deux
droites D1 et D2;
3°) Ensuite
: avec un rapporteur donner la valeur de l’angle faite par deux demi droites, quel commentaire
pouvez-vous avoir sur la position des droites l’une par rapport à l’autre.
INTERDISCIPLINARITES
: Voir problèmes de la vie quotidienne
(transport avec ou sans forfait ).