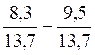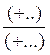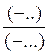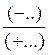Pré
requis
|
|
|
Mettre une écriture fractionnaire sous forme de fraction |
|
|
Savoir réduire au même dénominateur |
|
|
Soustraction deux
fractions de même dénominateur |
|
Expression d' un résultat
|
|
|
|
|
|
|
ENVIRONNEMENT du dossier :
|
Transformation en écriture
fractionnaire. |
|
Liste des cours sur « la soustraction
des .. » |
DOSSIER:
Leçon : SOUSTRACTION de deux
écritures fractionnaires de dénominateurs différents.
|
TEST |
COURS |
Interdisciplinarité |
|
Objectif : QIV soustraction niveau 6
soustraction de deux écritures fractionnaires.
Exemple : 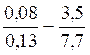
Procédure:
il faut d’ abord transformer les deux écritures
fractionnaires en fractions:
Si les
deux écritures fractionnaires ont le même dénominateur faire l’addition ou la
soustraction directement, transformer le résultat en fraction irréductible si
cela est demandé. Si non faire comme ci-dessous.
APPLICATION:
faire 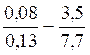
a)transformation des écritures fractionnaires en fractions:
première fraction: 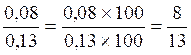 ;deuxième fraction::
;deuxième fraction:: 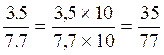
b)Poser la nouvelle égalité de deux fractions:
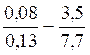 =
=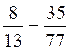
c)Rendre irréductible les fractions:
35 /
77 = 5 / 11 ;
8 / 13 est irréductible
d)reposer l’égalité:
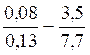 =
=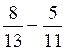
e)Calculer le PPDC de 13 et 11 :
13
Fois 11 = 143
F
) Transformation des fractions en fraction équivalente de dénominateur
égal à 143
8 / 13 = 8
fois 11 / 143 =
88 / 143
5 / 11 = 5
fois 13 143 = 85 /
143
g) On repose l’égalité et l’on fait le calcul (l’addition
)
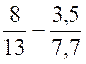 =
=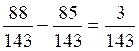
f) Rendre compte:
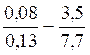 =
=![]()
|
Rappel : division entre deux nombres
relatifs |
|
|
|
Traduction des règles en
modèles mathématiques de la division d’un nombre relatif par un autre
nombre relatif : *Val3 est un
« rationnel » |
|
|
|
Même signe : ( + val
1 ) : ( + val2)
= ( + (val1 : val2 ) ) = + val3 ( - val
1 ) : ( - val2)
= ( + (val1 : val2 ) ) = + val3 |
Sous forme fractionnaire :
|
|
|
Signe contraire : ( - val 1 ) : ( + val2)
= (- (val1 : val2 ) ) = - val3 ( + val
1 ) : ( - val2) = ( - (val1 : val2
) ) = - val3 |
Sous forme fractionnaire :
|
|
CAS :
soustraction de deux écritures fractionnaires possédant des numérateurs et
dénominateurs « relatifs »
|
La différence |
Devient l’opération suivante |
|
|
(+..) - (+….)= Attention : la soustraction ne se fait pas !!! (@
voir la soustraction de deux nombres relatifs.) |
|
|
(+..) - (+….)= |
|
|
(+..) - (+….)= |
|
|
(-….) - (+….)= |
|
|
(-….) - (+….)= |
|
|
(-….) - (+….)= |
|
|
(-….) - (+….)= |
TRAVAUX AUTO FORMATIFS.
Donner la procédure permettant de passer d’une soustraction de deux écritures fractionnaires en une
soustraction de deux fractions de même dénominateur?
faire :( 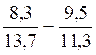 )
et
)
et