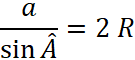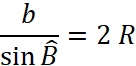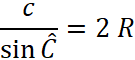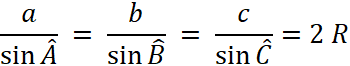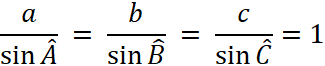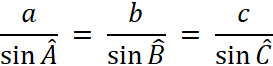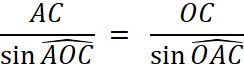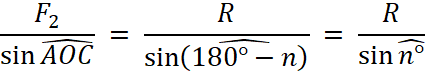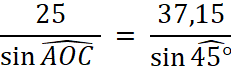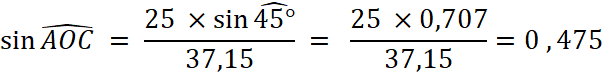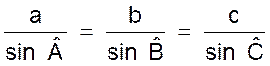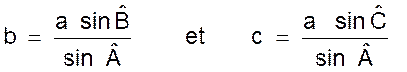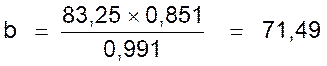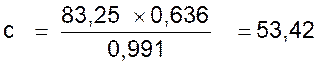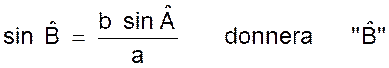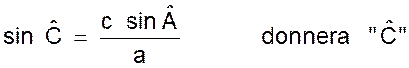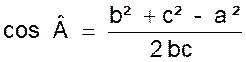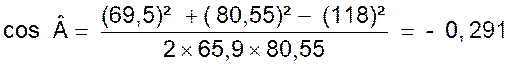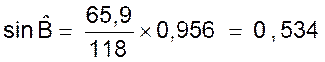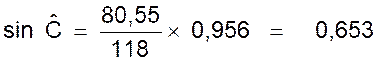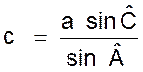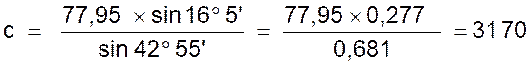Pré requis:		2 mars 2004 -WIMMEREUX -62
Les triangles quelconques.
ENVIRONNEMENT du dossier:
Index warmaths	Objectif précédent : 1°) Pythagore BEP 2°) Relations trigonométriques dans le triangle rectangle .		Objectif suivant 1°)Voir complément d’informations. 2°) Voir applications en arpentage .	Liste des cours de trigonométrie.

DOSSIER : LES RELATIONS trigonométriques entre les éléments d’un TRIANGLE QUELCONQUE.

Info sur les relations déjà connues utiliser pour la Résolution des triangles quelconques.

Info :Relation 1 :

Règle des sinus :

a / sin = b / sin = c / sin

Info : Relation 2 :

Info : Relation 3 :

.

Ces relations trigonométriques dans le triangle quelconque vont permettre de calculer la longueur ou la valeur d’un angle .

Nous verrons dans ce qui suit une APPLICATION de ces relations aux sciences : la résultante de deux forces.

Exemples de Résolutions de problèmes types :

Premier cas : Résoudre un triangle quelconque dont on connaît un côté « a » et les deux angles adjacents et

Deuxième cas  :Résoudre un triangle quelconque dont on connaît deux côtés « b » et « c » et l’angle .

Troisième cas : Résoudre un triangle quelconque dont on connaît les trois côtés « a » , « b » et « c » .

Quatrième cas : Résoudre un triangle quelconque dont on connaît deux côtés et l’angle opposé à l’un d’eux.

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

Applications des 3 relations trigonométriques aux triangles

Relation 1 : ( dit aussi «  la règle des sinus »)
Théorème  L à retenir.
Dans tout triangle les côtés sont proportionnels aux sinus des angles opposés.
Nous allons voir les deux cas .
Cas 1 :
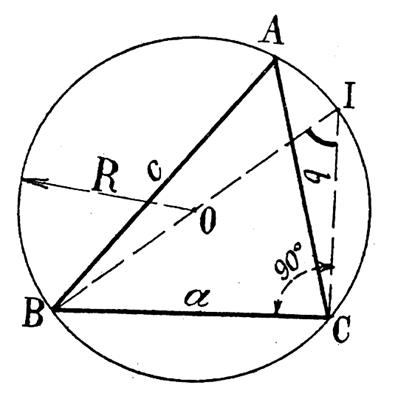
Considérons le triangle ABC et le cercle circonscrit « O ». Traçons le diamètre BI et joignons CI . Le triangle rectangle BCI donne : L’ angle est égal à l’angle Ces angles ayant la même mesure que l’arc :

Cas 2 :
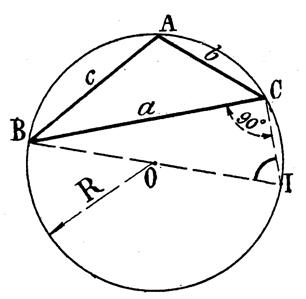
Considérons le triangle ABC et le cercle circonscrit « O ». Traçons le diamètre BI et joignons CI . Le triangle rectangle BCI donne : L’ angle est le supplément de l’angle obtus (quadrilatère ABIC inscrit )

Dans les deux cas nous avons :

Et l’ on peut écrire :

Ou :

Si « R » est le rayon du cercle inscrit on peut écrire :

On en déduit :

On a donc finalement :

Et si «  2 R = D » ( R = rayon ; 2 R = D = diamètre) et si «  D = 1 » alors :

Et finalement :

Relation 2  :
Dans un triangle quelconque, chaque côté est égal à la somme des produits des deux autres par le cosinus de l’angle qu’ils forment avec le premier côté.
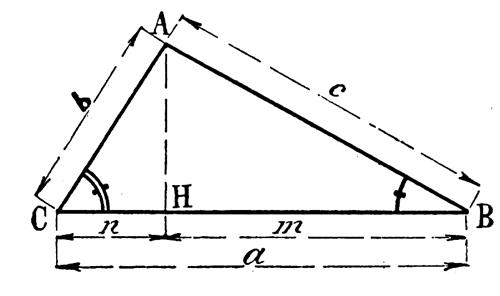
Si l’on mène la hauteur « AH » relative au côté « a »on a immédiatement : ( 1 )
On en déduit par analogie :
(2 )
( 3 )
Remarque : La démonstration suppose un triangle ayant et aigus .
Si l’un des angles par exemple est obtus on a le cas qui donne : Or : ( voir des angles supplémentaires) En remplaçant on aura encore : Ou (on retrouve la formule du premier cas)

Relation n°3 :
Théorème : Dans un triangle quelconque le carré de chaque côté est égal à la somme des carrés des deux autres côtés , moins le double produit de ces côtés par le cosinus de l’angle qu’ils comprennent.
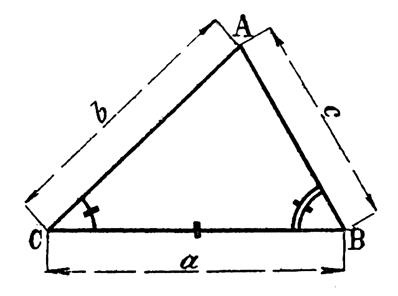
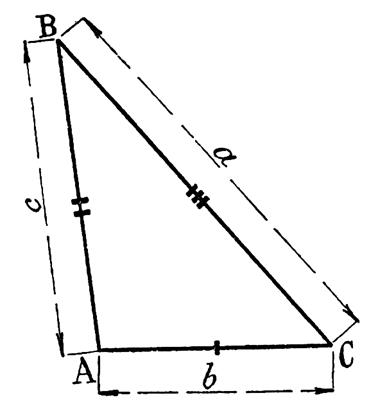
En désignant par « a » , « b » et « c » les côtés d’un triangle et par « p » la projection de « b » sur « c » , on peut écrire d’après un théorème de géométrie .
(@ info, sur les triangles quelconques ) :
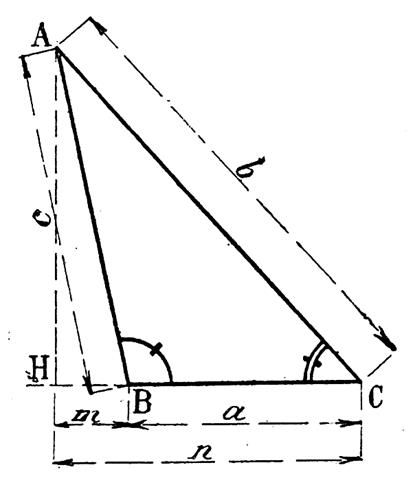
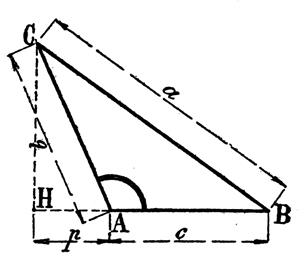
Suivant le cas :
Le signe est + si « a » est opposé à un angle obtus	Le signe est si « a » est opposé à un angle aigu
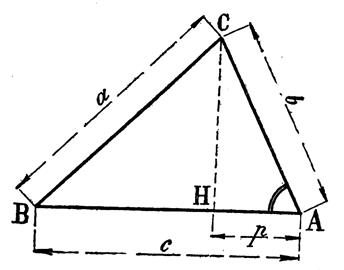
Pour l’angle obtus :	Pour l’angle aigu :
ou
ou	ou
Ou :
Ainsi les deux formules de (1) sont donc réduites à la forme unique :
( 2 )
On aurait en analogie :
(3) b² = a² + c² - 2 a c cos
(4) c² = a² + b² - 2 a b cos
Ces formules permettent le calcul du 3ème côté d’un triangle connaissant les deux autres côtés et l’angle qu’ils comprennent.

	APPLICATION :
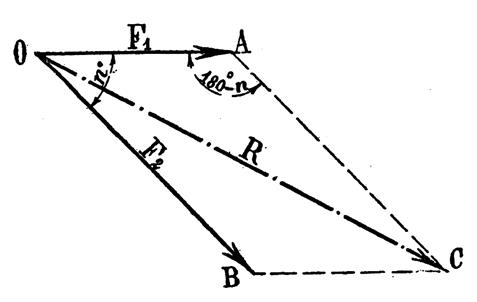
	(en sciences) Détermination de la résultante de deux forces. En mécanique lorsque l’on veut déterminer la résultante « R » de deux forces F1 et F2 faisant entre elles un angle quelconque « O » il suffit d’appliquer la relation précédente du parallélogramme des forces.
		On peut établir la relation : R² = F1² + F 2² - 2 F1 F 2 ( ) Exemple : si F1 = 15 N F 2 = 25 N et L’angle = 45° . On trouvera : R² = 1380,25 R = 37 ,15 N
Info notation	a) Valeur de la résultante : On considère par exemple Le triangle OAC : On établit la relation suivante , à partir de ce que nous avons vu précédemment :
	( lire mesure algébrique du bi point AB )
	=
	En remplaçant les segments précédents par leurs valeurs respectives et en remarquant que cos A = - cos ( angles supplémentaires) , on a finalement : R² = F1² + F 2² - 2 F1 ´ F 2 ( - cos ) R² = F1² + F 2² + 2 F1 ´ F 2 ´ cos ( 1) Si par exemple : si F1 = 15 N ; F 2 = 25 N et L’angle = 45° . (d ‘après la table : cos 45° =0,707) , on remplace dans (1) On aura : R² = 15 ² + 25 ² + 2 ´ 15 ´ 25 ´ 0 ,707 R² = 225 + 625 + 750 ´ 0 ,707 R² = 850 + 750 ´ 0 ,707 On trouvera : R² = 1380,25 On fait ensuite la racine carrée de R² : R = 37 ,15 N
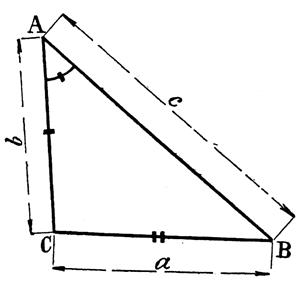
	B ) Direction de la résultante :
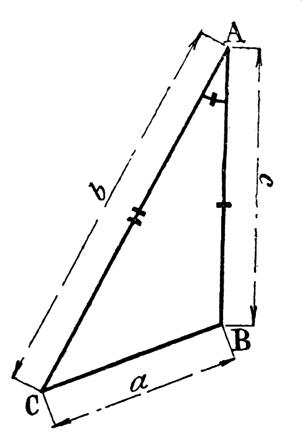
	La relation du sinus permet d’autre part de calculer l’inclinaison de la résultante par rapport à l’une quelconque des forces. Le triangle OAC donne en effet : Ou
	En remplaçant par les valeurs données ou calculées  et d’établir  l’égalité suivante :
	Calcul :
	D ‘après la table (ou la calculatrice) : on trouvera  que le sinus de l’angle AOC = 28°20’ nota : En appliquant la vérification sur la somme des angles d’un triangle , on constatera que l’angle obtus supplément de l’angle AOC ne convient pas .
	L’exemple précédent est un exemple de résolution d’un triangle quelconque connaissant deux côtés et l’angle compris . Les différents cas de résolution qui peuvent se présenter dans la pratique sont traités dans les pages suivantes.

Les 4 ( cas ) EXERCICES types : RESOLUTION des triangles quelconques.

Premier cas : Résoudre un triangle quelconque dont on connaît un côté « a » et les deux angles adjacents et .
Les données sont : « a » = 83,25 m = 39° 30’ = 58° 20’	Les inconnues sont donc : « b » , « c » , et l’angle A.
Formules de résolution. A = 180° - ( + )
on en tire les deux égalités suivantes :
Calcul de l’angle  :
= 180° - ( + )		= 180° - (39° 30’+ 58° 20’ )		= 82° 10’
Calcul de « b » : Sin 58° 20’ = 0,851 ; sinus 82° 10’= 0,991
Calcul de « c » : Sin 39° 30’ = 0,636 ; sinus 82° 10’= 0,991

Deuxième cas : Résoudre un triangle quelconque dont on connaît deux côtés « b » et « c » et l’angle .
Les données sont : « b » = 160,60 m « c » = 112 , 90 m = 26° 15	Les inconnues sont donc : « a » =  ? = ? =  ?
Formules de résolution.
a² = b² + c² - 2 c b cos (donnera « a » )
Dont on tire
Calcul de « a » : ( cos 26° 15 ‘ = 0,897)
a² = ( 160,60 ) ² + ( 112,90)² - 2 ´ 160,60 ´ 112,90 ´ cos 26° 15’ a² = ( 160,60 ) ² + ( 112,90)² - 2 ´ 160,60 ´ 112,90 ´ 0,897 a² = 38538,77 - 32 528,34 = 6010,43 « a » = 77,50 m
Calcul de sinus de l’angle B pour en déduire l’angle B.
Sin 26° 15’ = 0,442 sin = 0,916 On trouve = 66° 20 ‘ ou = 180 ° - 66° 20 ‘ = 113° 40’
Calcul de sinus de l’angle pour en déduire l’angle
sin = 0,644 ; d’où = 40° 5’ ou = 180° - 40° 5’ ; = 139° 55’
On vérifiera que «  + + = 180 ° » Les valeurs de = 66° 20 ‘ et = 139° 55’ sont à rejeter , car elles ne permettent pas de satisfaire à la relation + + = 180 °

Troisième cas : Résoudre un triangle quelconque dont on connaît les trois côtés « a » , « b » et « c » .
Les données sont : « b » =  118 m « c » =  65 ,90 m « a » =  80,55 m	Les inconnues sont donc : = ? =  ? = ?
Formules de résolution :
a² = b² + c² - 2 c b cos et de cette formule on tire : 2 c b cos = b² + c² - a² et
trouver dans la table , on en déduit et ; par la relation des sinus :
par transformation , on trouvera :
Calculs :
Calcul de l’angle  :
pour 0,291 sur la table on lit : 73° 5’ ; et pour - 0,291 : l’angle = 180° - 73° 5’ = 106 ° 55 ‘ L’angle = 106 ° 55 ‘ pour le calcul de , sur la table on lira le sin = sin 106° 55’ = sin 73° 5’ ; et sinus 73° 5’ = 0,956
Calcul de l’ angle
: on utilise la formule
Pour 0,534 l’ angle = 32 ° 17 ‘
Calcul de l’ angle :
On utilise la formule
D ‘ après la calculatrice pour 0,653 on trouve l’angle C = = 40 ° 45’ Nota : les suppléments des angles B et C ne conviennent pas . (voir vérification avec la somme des angles dans un triangle)

Quatrième cas :
(deux exemples sont proposés : le premier débouche sur un ensemble de solutions . Le second exemple débouche sur deux ensembles de solutions possibles)
Résoudre un triangle quelconque dont on connaît deux côtés et l’angle opposé à l’un d’eux.
Les données : « a » « b » l’angle A. ( )	Les inconnues sont : L’angle B ( ) L’angle C « c »
Les formules de résolution sont :
( la valeur en degré de l’angle B s’obtient au moyen de la calculatrice ou d’une table.)
Puis l’angle = 180° - ( + )
Et
Exemple premier : un seul ensemble de solutions :
Exemple numérique : « a » = 95,75m « b » = 70,40 m = 49° 40’
Calcul de l’angle :
d’après la calculatrice : à 0,560 correspond l’angle : 34°3’
Calcul de l’angle  :
= 180° - ( 49° 40’ + 34° 3’ ) soit = 96° 17’
Calcul de « c » :
Sin 96° 17’ = sin ( 180° - 96° 17’) = sin 83° 43’ (@ info. +) Et sin 83° 43’ = 0,994
le côté c = 124,90 m
Pour sinus B = 0,560 une deuxième valeur de B est 180° - 34° 3’ = 145° 57’. (@ info+)
Mais alors + + > 180° par suite cette deuxième valeur de B ne convient pas , ne répond pas à la question. Avec les données suivantes on peut voir que deux solutions sont acceptables.
Exemple second  : on peut proposer deux ensembles de solutions :
On donne : « a » = 77,95 m ; « b » = 98,10 m et l’angle A = 42°55’
Calcul de l’angle  :
Pour calculer l’angle on a besoin du sinus de l’angle : sin 42°55’ = 0,681
pour 0,851 , on a ou = 59° ou = 121 ° (soit 2 possibilités)
Calcul de l’angle
2 cas
Cas 1°) = 180° - ( + ) avec = 59°
= 180° - ( 42° 55’ + 59 ° ) soit = 78° 5’
Cas 2°) = 180° - ( + ) avec = 121°
= 180° - ( 42° 55’ + 121 ° ) soit = 16 ° 5’
On trouve 2 valeurs pour l’angle B et pour l’angle : Vérifications : Cas 1 : 42° 55’ + 59 ° + 78°5’ = 180° Cas 2 : 42° 55’ + 121° + 16° 5’ = 180°
Calcul de la longueur de « c »
Cas1 : Soit « c » = 112,06 m
Ou deuxième solution :
Cas 2
Soit « c » = 31,70 m

Revu le 29 / 03 / 2020

Voir les travaux auto formatifs….