@

Leçon LES RAPPORTS TRIGONOMETRIQUES

1°) Propriété fondamentale : ( @ info : division de segments)
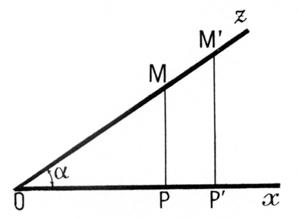
Considérons un angle aigu « x O z » égal à alpha « a ». Soit « M » un point quelconque de « Oz » et « P » sa projection orthogonale sur « Ox ». Le triangle rectangle OPM reste semblable à lui -même lorsque « M » parcours « Oz ». et s’arrête par exemple en « M’ » Donc : On en déduit les trois proportions

Le rapport de deux côtés du triangles OPM est donc indépendant de la position du point M et reste constant lorsque M parcours « Oz » Inversement si on connaît la valeur de l’un de ces rapports on pourra construire un triangle O’P’M’ semblable à OPM et par suite construire l’angle « a ».
2°) Rapports trigonométriques d’un angle aigu .
Les trois rapports indépendant du point M , caractérisent l’angle aigu « a ». On les appelle respectivement cosinus , sinus et tangente de l’angle aigu « a ». On aurait pu envisager aussi les inverses de ces trois rapports. Pratiquement on n’utilise que l’inverse du dernier qui se nomme « cotangente de l’angle« a ». Les deux autres rapports se nomment : « sécante » et « cosécante »
On écrit en abrégé : cos lire « cosinus » ; sin lire « sinus » , tan lire tangente , cotan lire « cotangente »

Les sin x ; cos x ; tan x et cotan x constituent les rapports trigonométriques de l’angle x.
3°) Interprétation géométrique
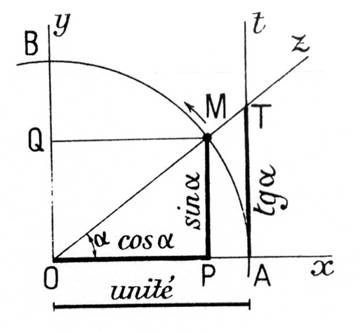
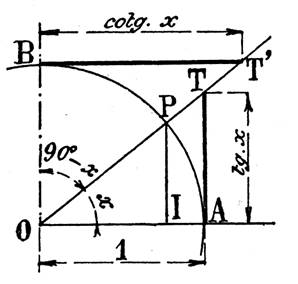
Nous désignons par A et M les intersections des demi droites O z et O x avec le cercle de centre O et de rayon 1 . (figure ci contre) Nous désignons par T l’intersection de la tangente en A avec la demi droite Oz . Puisque OA = OM = 1 , il en résulte que :

soit	Soit		Soit
sin a = PM	cos a = OP		tan a = AT
Nous remarquons que l’arc AM intercepté par l’angle « xOz » a pour mesure «a » C’est pourquoi on parle indifféremment des rapports trigonométriques d’un angle ou d’un arc. D’autre part , si on désigne par « Q » la projection orthogonale de M sur la demi droite Oy on a : Sin a = OQ Remarque importante : il faut éviter de supposer ici que sin a; cos a , tan a sont des segments. Il faut au contraire dans la formule cos a = OP supposer que OP représente la mesure du segment OP , c’est à dire le « rapport du segment OP au segment unité OA ou OM .
4°) Variations des rapports trigonométriques.. ( @ info +++)
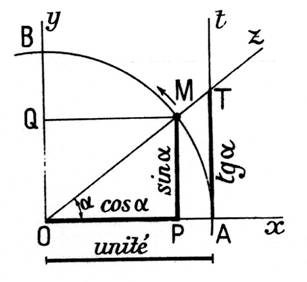
Si l’angle alpha ( a) varie de 0° à 90° (voir figure ci dessus) , le point M décrit le quart de cercle AB . Il est visible que : « P » décrit le segment AO . Donc cos a décroît de +1 à 0 « Q » décrit le segment OB , donc sinus a croît de 0 à +1 « T » décrit la demi droite A t , donc tan a croît de 0 à + ¥ et son inverse cotan a décroît de + ¥ à 0. Noter que le sinus et le cosinus d’un angle aigu sont compris entre 0 et 1 .
5°) Relations entre les rapports trigonométriques de l’angle a .
Les rapports trigonométriques de l’angle a sont liés par les 3 relations suivantes(@Linfo+)
Relation 1		Relation 2		Relation 3
Cos ² a + sin ² a = 1

1°) Considérons le triangle OMP ( voir ci contre et ci dessus). D’après la relation de Pythagore : + = or OP = cos a , PM = OQ = sin a et OM = 1 donc : ( cos a ) ² + ( sin a ) ² = 1 par convention on écrit : ( cos a ) ² = cos ² a et on lit « cosinus carré alpha » afin de ne pas confondre avec cos ( a ) ² ou cos ( 2 a ) .
2°) Les triangles OPM et OAT sont semblables :
Soit :
3°) La formule de définition :

Théorème : lorsque deux angles sont complémentaires : - le sinus de l’un et égal au cosinus de l’autre. - La tangente de l’un est égale à la cotangente de l’autre.
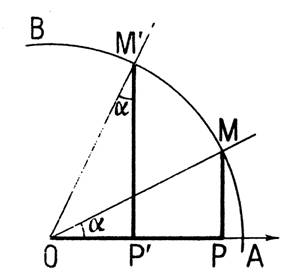
Soient AOM = a et A O M’ = a ‘ deux angles aigus complémentaires ( figure ci contre) . Les deux triangles rectangles OPM et M’P’O ont l’hypoténuse égale et leurs angles aigus respectivement égaux à a et à a ‘ . Ils sont égaux et PM = OP’ et OP = P’M’ soit sin a = cos a’ et cos a = sin a’ En faisant les rapports membre à membre de ces deux égalités ont obtient : tan a = cotan a’ et cotan a = tan a’


6°) Usage des tables de rapports trigonométriques
(@ table de rapports )
Les tables de rapports trigonométriques fournissent des nombres en relation avec les angles aigus. Ces tables informent de degrés en degrés ou de grades en grades. Ces tables se lisent de haut en bas pour les angles inférieurs à 45° ou 50 grades , et de bas en haut pour les angles supérieurs à 45 ° ou 50 grades.
Leur emploi est immédiat pour les nombres figurant dans la table : Tan 38° = 0,7813 ; 0, 8746 = cos 29° = sin 61°
Si nous ne possédons pas de calculatrice scientifique. Pour les autres valeurs on procède par interpolation en admettant que : Entre deux valeurs consécutives de la table , l’accroissement de l’angle et l’accroissement d’un rapport trigonométrique sont proportionnels (nous accepterons même si cela n’est pas exacte en vérité) Ces accroissement doivent être pris en valeur algébrique.
Problème N°1 : Déterminer : sin 32° 25 ‘ et cos 32° 25 ‘ a) sin 32° 25 ‘ ? On lit dans la table : sin 32° = 0,5299 ; sin 33° = 0,5446 Pour un accroissement de 1° = 60’ , l’accroissement du sinus est ( en dix millièmes) : D = 446 - 299 = 147 . Pour un accroissement de 1’ cet accroissement serait de ( 147 / 60 ) et pour 25 ‘ la correction est donc : (147 fois 25) / 60 = 61,25 On arrondit à 61 , ce qui donne , sinus 32° 25 ‘ = 0,5299 + 0,0061 = 0,5360 b ) cos 32° 25 ‘ On opère de même pour le cosinus : seuls différence , D est négatif ainsi que la correction. On trouvera pour cos 32° 25’ = 0,8442.
Problème N°2 : déterminer a sachant que tan a = 0,7456.
On lit dans la table : 0,7265 = tan 36° et 0,7536 = tan 37° Quand tan a s’accroît de D = 536 - 265 = 271 , a s’accroît de 1° = 60 ‘ Pour un accroissement de 456 - 265 = 191 la correction pour a sera de ( 60 ‘ fois 191) divisé par 271 = 42 ‘ D’où a = 36°42
Les calculs sont analogues lorsqu ‘ on opère en grades ( il faut remplacer 60 par 10 pour les décigrades ou 100 pour les centigrades).

TRAVAUX AUTO FORMATIFS.
CONTROLE :
Citer les 4 rapports trigonométriques.
EVALUATION :

1°) Donner avec la table et la calculatrice les rapports trigonométriques des angles suivants :
25° =		31°=		43°=
57°=		81°=		83°=

2°) Déterminer l’angle aigu « x » tel que :
Sin x = 0,48		Cos x = 0,1550		Tan x = 0,3
Sin x = 0,84		Cos x = 0,9515		Tan x = 1,5




3°) Soit un angle aigu xOy tel que sin xOy = 3/5 a) sans se servir de la table, calculer cos xOy et tan xOy b) construire géométriquement cet angle .

Voir les exercices : ci @ info

Compléments sur la « sécante » et la « cosécante » d’un angle aigu.
Voir figure ci contre : La sécante d’un angle « x » est le rapport de l’hypoténuse au côté de l’angle droit adjacent à « x » et l’on écrit : la cosécante d’un angle « x » est le rapport de l’hypoténuse OP au côté de l’angle droit opposé à « x » d’ où :
Remarque : dans la figure ci dessus on a :
Et

Fin du complément.