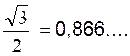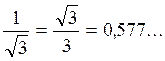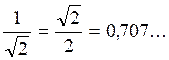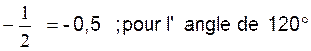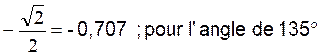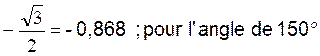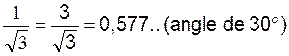Pré requis:
Variation d’un angle aigu.
Tracés d’une sinusoïde
Cercle trigonométrique
ENVIRONNEMENT du dossier:
Index warmaths		Objectif précédent : Info sur les tracés d’une sinusoïde …..				Objectif suivant Retour vers la trigonométrie ..			Tout sur la trigonométrie.
DOSSIER : VARIATIONS des NOMBRES TRIGONOMETRIQUES 1°) Variation d’un angle aigu ( compris entre 0° et 90°) 2°) Variation d’un angle obtus ( compris entre 0° et 180°) 3°) Représentations graphiques des variations des rapports trigonométriques ces angles ou des arcs croissants entre 0° et 180°. 4°) Représentations graphiques des variations des rapports trigonométriques ces angles ou des arcs croissants entre 0° et 360°. A) variation du sinus. ( et sinusoïde) B) Variation du cosinus. C) Variation de la tangente ( et asymptote) D) Variation de la cotangente.
TEST	COURS		Devoir Contrôle		Devoir évaluation		Interdisciplinarité	Corrigé Contrôle		Corrigé évaluation

COURS

1°) Variation d’un angle aigu ( compris entre 0° et 90°)
Les valeurs trouvées dans le cours « pré requis » ont permis de dresser le tableau suivant qui donne une première idée de la variation des lignes trigonométriques d’un angle aigu :
ANGLES	Sinus	Cosinus		Tangente	cotangente
▼	Augmente de +1 à 0	Diminue de +1 à 0		Augmente de 0 à + ¥	Diminue de + ¥ à 0
0°	0	+1		0	+ ¥
30°
45°				+1	+1
60°
90°	+1	0		+ ¥	0
2°) Variation d’un angle obtus ( compris entre 0° et 180°)
L’étude de variation des nombres trigonométriques se limitera à la variation de l’angle « x » . (pour ses valeurs de « x » q comprises entre 0 et 180 ° ou entre 0 et 200 grades ou entre 0 et p ) .

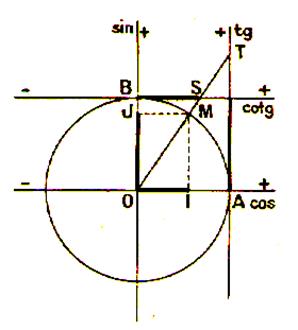
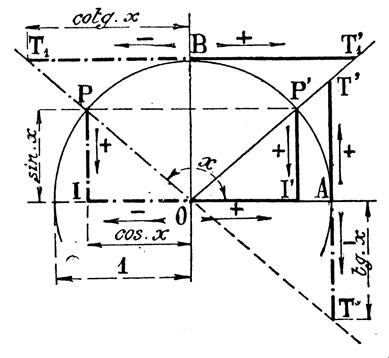
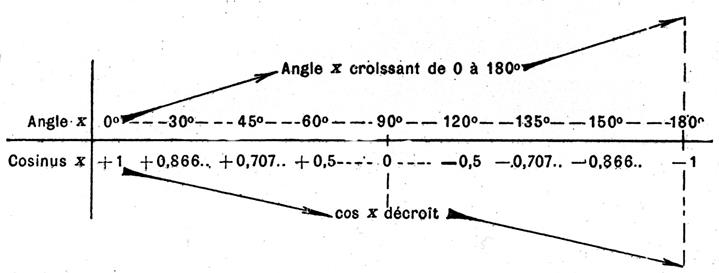
Rappels : « Cos x° » le nombre mesurant l’abscisse «  x = OI ou OI’  » ,par rapport au rayon « sin x° » le nombre mesurant l’ordonnée «  y =IP ou I’P’ » ,par rapport au rayon « tan x  ou tg x » le nombre mesurant le segment « u = ou A’T’  » par rapport au rayon.  « cotan x ou cotg x » le nombre mesurant le segment « v = BT1 ou B’T’1 » par rapport au rayon.
3°) Représentations graphiques des variations des rapports trigonométriques ces angles ou des arcs croissants entre 0° et 180°.
Variation du cos	Variation du sinus
Variation de la cotangente	Variation de la tangente.

4°) Représentations graphiques des variations des rapports trigonométriques ces angles ou des arcs croissants entre 0° et 360°.

Nous allons préciser les notions précédentes et les compléter par une représentation graphique des variations des rapports trigonométriques des angles ou des arcs croissant de 0 à 180° puis de 180° à 360°.

A) Variation du sinus :

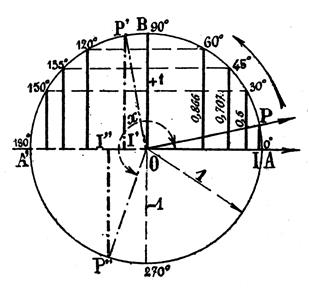
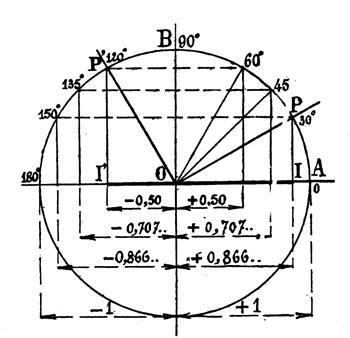
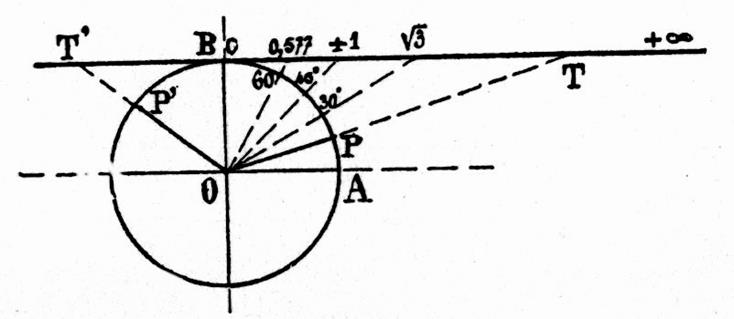
Considérons le cercle trigonométrique et soit l’angle variable «  » formé par la direction fixe OA et par la direction variable OP tournant autour du centre « O ». - L’angle est croissant de 0° à 90 ° , son sinus « PI » croît de 0 à +1 en passant par des valeurs remarquables :

« 0,5 » pour l’angle de 30°

Pour l’angle der 45°

Pour l’angle de 60°

- L’angle continue à croître de 90° à 180 ° , son sinus « P’I’ » décroît de +1 à 0 en passant par des valeurs remarquables précédentes , pour les suppléments des angles considérés:

Pour l’angle de 120°

Pour l’angle der 135°

« 0,5 » pour l’angle de 150°

Remarque : Si l’on continue à faire tourner OP de manière à obtenir des arcs et par suite des angles supérieurs à 180° , on voit que le sinus P’’I’’ d’un de ces angles « x » se mesure en dessous du diamètre AA’ ; on convient de la considérer comme négatif .En conséquence pour un arc ou un angle croissant de 180° à 270° le sinus décroît de 0 à -1 , et pour un arc ou un angle croissant de 270° à 360° , le sinus croît de -1 à 0 .

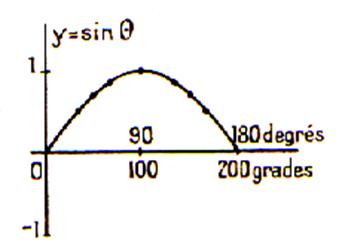
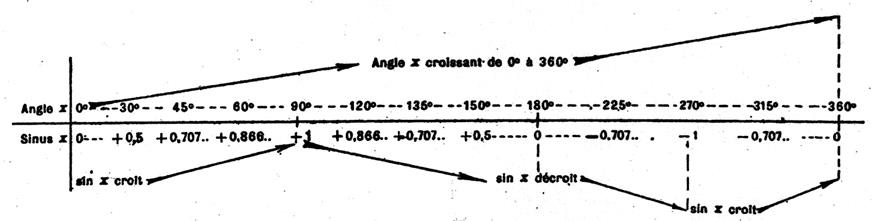
Tableau de variation du sinus : Les variations du sinus d’arc ou d’un angle croissant de 0° à 360° sont résumées dans le tableau ci dessous :

Il résulte de l’étude précédente que le sinus d’un angle inférieur à 180° passe 2 fois par chacune des valeurs compris entre 0 et +1 . Donc, à un sinus positif donné, qui doit être inférieur à +1 , correspondent deux angles distincts qui sont supplémentaires.

Exemple : si l’on a sinus x° = 0,347 , les deux angles supplémentaires ayant cette valeur pour leur sinus sont : « x1 °= 20° 20’ » et « x 2 ° = 159° 40 ‘ » (voir calculatrice ou la table)

Représentation graphique de la variation du sinus d’un angle croissant de 0° à 180° et de 180° à 360°.

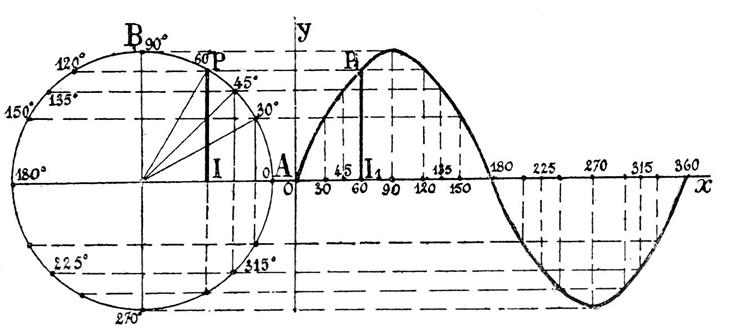
Si nous considérons 2 axes rectangulaires « ox » et « oy » , la circonférence de rayon « 1 » ayant été divisé e en 12 parties égales par exemple, on porte sur « ox » à partir du point O , douze segments égaux. En mesurant les segments successifs ayant 0 pour origine , 0-30 ; 0-60 ; 0 - 90 ; 0 - 120 ;etc. on aura des longueurs proportionnelles aux divers arcs ou angles de 30° ; 60° ; 90° ; 120°, etc. Le graphite est compété par les divisions correspondants aux angles de 45° ; 135° ; 225° ; et 315° .

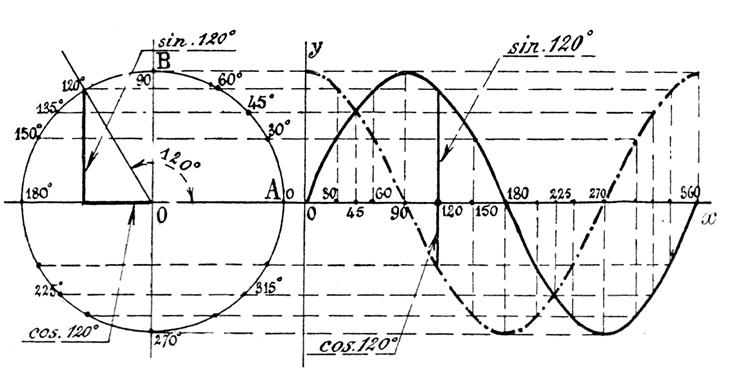
En chaque point de « ox » on élève à cette droite une perpendiculaire appelée « ordonnée » , égale au sinus correspondant à l’angle variable considéré. C’est ainsi que PI , sinus de 60° , a été reporté en P1 I1 au point correspondant à l’arc de 60°. En réunissant par un trait continu tous les points tels que P1 , on obtient une courbe appelée « sinusoïde » représentant la variation du sinus d’un angle croissant de 0° à 360°. Remarque : Les différents points sont en somme , comme l’indique la figure ci dessus , déterminés par les intersections des parallèles aux axes « ox » et « oy » , menées par les points de divisions correspondants du cercle et de l’axe « ox ». Ce graphique est utilisé en électricité pour la représentation des courbes de courant alternatif. ( Courbes sinusoïdales).

B ) Variation du cosinus.

Lorsqu ‘un angle «  » croît de 0° à 90° son cosinus « OI » décroît de +1 à 0 en passant par des valeurs remarquables.

Pour l’angle de 30°

Pour l’angle de 45°

« 0,5 » pour l’angle de 60°

Si l’angle «  » continue à croître de 90° à 180° son cosinus OI’ devient négatif et continue à décroître de 0 à -1 en passant par les valeurs remarquables.

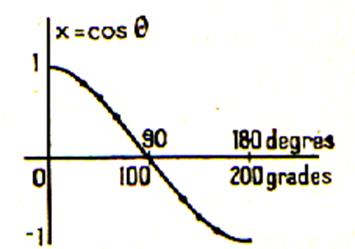
Tableau de variation du cosinus. Les variations du cosinus d’un arc ou d’un angle croissant de 0° à 180° sont résumées dans le tableau ci dessous.

De l’étude précédente , il résulte que le cosinus d’un angle inférieur à 180° passe une fois seulement par chacune des valeurs comprises entre +1 et -1. Donc à un cosinus donné positif ou négatif de valeur absolue inférieur à 1 correspond un angle et un seul.

Exemple : S’il l’on a cos x° = 0,636 , on trouve pour valeur de « x » d’après la table : 50° 30’. L’angle dont le cosinus vaut - 0,636 est le supplément du précédent il vaut donc 129° 30’.

Représentation graphique de la variation du cosinus .

La représentation graphique de la variation du cosinus se ferait aussi facilement que celle du sinus et donnerait une courbe de forme identique. Le graphique représenté ci dessous donne à la fois les courbes de variation du « sinus » (trait continu) et du cosinus (trait mixte) d’un même angle.

L’étude du courant alternatif en électricité donne lieu à des graphiques analogues à celui de la figure ci dessus, notamment en représentation des courants diphasés..

Remarque : Les deux « sinusoïdes » représentant les variations du « sinus » et du « cosinus » d’un même angle sont identiques (voir ci dessus) , mais l’ordonnée de la courbe représentative du sinus est nulle au point « origine » alors que celle de la courbe du cosinus est à son maximum +1 ; ces valeurs « 0 » et « ± 1 » se correspondent à nouveau pour chaque angle multiple de 90° ; on dit que la courbe représentative du « sinus » est décalée de 90° sur la courbe représentative du cosinus ou encore que les deux courbes sont en « quadrature ». L’étude des courants triphasés en électricité donne lieu à des graphiques comportant trois sinusoïdes décalées de 120° l’une par rapport à l’autre .

C) Variation de la tangente.

Lorsqu ‘un angle «  » croît de 0° à 90° la tangente « AT » croît de 0 à + ¥ en passant par des valeurs remarquables :

1 (angle de 45°)

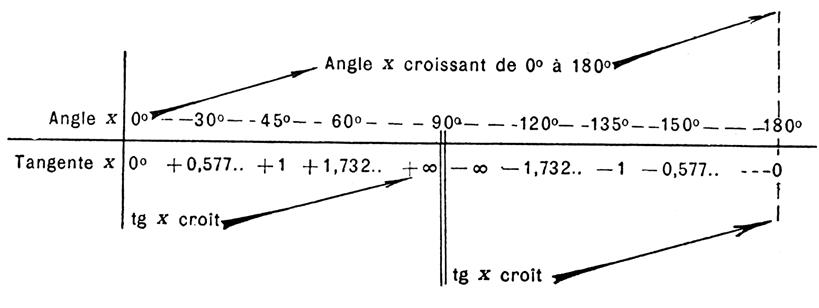
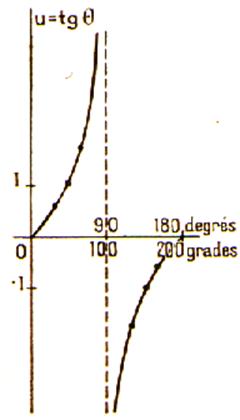
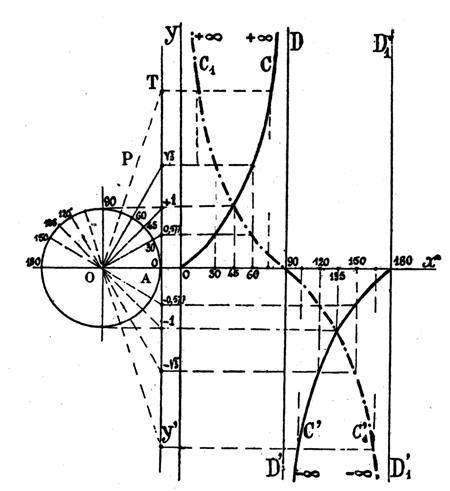
Si l’angle continue à croître de 90° à 180° la tangente devient négative et , partant d’une valeur négative égale à -¥ , croît algébriquement de -¥ à 0 , en repassant par les valeurs remarquables précédentes mais négatives. Ces variations de la tangente d’un angle croissant de 0° à 180° sont résumées dans le tableau ci dessous. La figure ci contre donne la représentation graphique des variations de la tangente (trait continu) et de la cotangente ( trait mixte) d’un angle croissant de 0° à 180°.

De ce qui précède , il résulte que la tangente d’un angle inférieur à 180° passe une fois seulement par une valeur donnée positive ou négative. Donc une tangente donnée , positive ou négative correspond un angle et un seul. Exemple : si l’on a tan x = 1,402 , la table donne une valeur de « x » = 54° 30’ l’angle dont la tangente est égale à « -1, 402 » est le supplément du précédent , il est donc égal à 125° 30’

D) Variation de la cotangente.

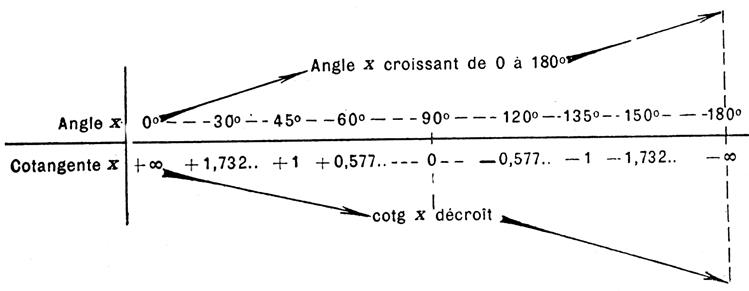
Lorsqu ‘un angle «  » croît de 0° à 90° , la cotangente « BT » décroît de + ¥ à 0 . L’angle croissant de 90° à 180° la cotangente BT’ continue à décroître algébriquement de 0 à - ¥

Entre + ¥ et - ¥ la cotangente passe d’ailleurs par les valeurs remarquables données pour la tangente , comme l’indique le tableau des variations ci dessus.

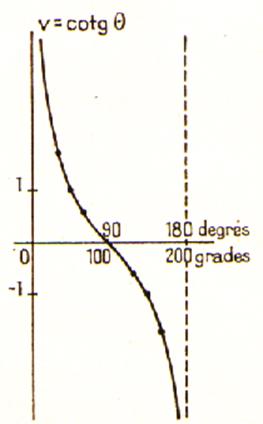
Comme pour la tangente et pour un angle inférieur à 180° , on voit qu’à une cotangente donnée quelconque , positive ou négative , correspond toujours un angle et un seul.

Exemple : si l’on a cotan x = 0,452 avec la calculatrice on a pour valeur de x = 65° 40’. L’angle dont la cotangente est égale à - 0,452 est le supplément du précédent il est donc égal à 114° 20’

Représentation graphique : ( voir la figure concernant la tangente )elle donne la représentation graphique des variations de la tangente (trait continu) et de la cotangente ( trait mixte) d’un angle croissant de 0° à 180°. Les points importants de ces courbes ont été déterminés par des parallèles aux axes « ox » et « oy » menées respectivement par les points correspondants de la tanegente au cercle et de l’axe « ox ». Comme les graphiques l’indiquent , les branches de courbes de la tangente se rapproche de plus en plus de la perpendiculaire DD’ à « ox » passant par le point correspondant à 90°, sans toutefois attendre cette droite quelle que soit la valeur de l’angle considéré. On dit en géométrie que la droite DD’ est une « asymptote » aux courbes C et C’ . On voit de même que la courbe C1 C’1 représentative de la cotangente a pour « asymptote » y y’ et D1 D’1.

CONTROLE:

EVALUATION: