Fiche 1 :   Figures se correspondant par une rotation.

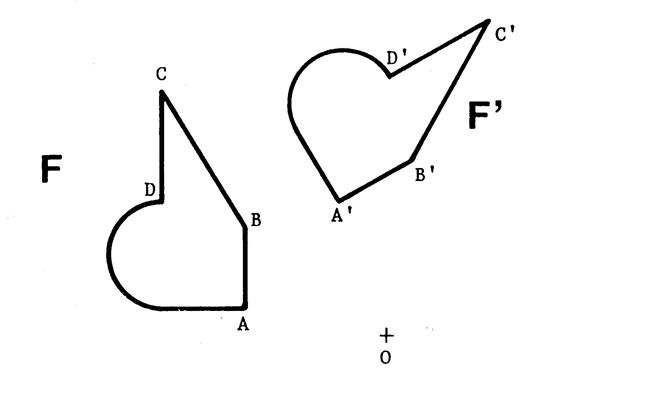
Voici  ci-dessous deux figures F et F' et un point 0.

Activité :

Prenez une feuille de papier calque et calquez la figure « F » et le point « 0 ».
Sans bouger le calque, piquez  la pointe de votre  compas au point « 0 ».
Ensuite faites tourner le calque de telle sorte que le dessin de « F » vienne sur « F’ ».
Que constatez – vous  pour « F' » et le dessin de « F » ?                                  .                                  

Ce que l'on traduit en disant que les figures « F » et « F’ »  sont …………superposables…………………

On dit que l'on est passé de la figure « F » à la figure «F ‘ »  par une rotation de centre « 0 »

Ø Pour matérialiser le déplacement de certains  points    (« A » , « B » , « C » , « D »  par exemple), tracez les arcs de cercle  ,   ,  ,  de centre 0.

Le point « 0 »   n'a pas bougé, le point  « A »  est venu en « A' »  on a alors « OA…….OA' ».

Ø Mesurez  l'angle        .  Vous  trouvez   ……..°.

De même, mesure BOB¹ , COC' , DOD'.  Vous  trouvez  toujours .. ……..°.

Et vous  avez  aussi :     OB OB'   ;   OC   OC' ;  OD  OD'.

Il en serait de même pour tout point de « F » et de son correspondant sur « F’ » . On dit que « F' » est l'image de « F » dans la rotation de centre « 0 » et d'angle 60°.

* D'une manière générale, on dira :

à retenir :

                    Etant donné, un point « 0 » et un angle, de      ;

(    )

  la figure « F’ » est l’image  de la figure « F » dans la rotation de centre « O » de d’angle   , signifie que :

                Tout point « M’ » de « F’ »est obtenu à partir d’un point « M » de « F » de telle sorte que  «  OM’ = OM »  et

(en tournant autour de « O » dans un sens déterminé , le  même, pour i tous les  points. )

Remarque : Toute  figure et son image par une rotation sont superposables

Remarque

« F' » est l'image de « F »  dans la rotation de centre 0 et d'angle 60°  en tournant dans le sens des aiguilles d'une montre.

« F » est l'image de « F' »  dans la rotation ……………………………….en  tournant ……………………………………………….

Activité :

En utilisant le même morceau de calque que précédemment   (après avoir passé au crayon gris l'envers du dessin de F), dessinez  l'image « F" » de  « F » dans la rotation de centre « O »  et d'angle 130°.

( vous pouvez  prendre des repères sur la feuille pour faire tourner le calque de 130°)

Rotation de 180° :

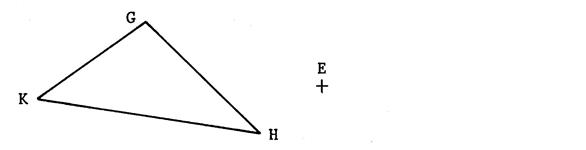
                                           Toujours en utilisant le papier calque , dessinez ( comme précédemment ) l’image du triangle « GHK » dans la rotation de centre « E » et d’angle « 180° »

Appelez « G’ » l’image de « G » , « H’ » l’image de « H » , et « K’ » l’image de « K ».

·       L’angle de la rotation étant de 180° alors donc  « G » , « E » , « G’ » sont alignés.

De même    ,   donc « H » , « E » ,  « H’ »  sont ……………….ainsi  « K » , « E » , « K’ ».

Puisque  « G » , « E » , « G’ » sont alignés et  que  «    alors « E » est le  centre  de   .

On peut affirmer de même que  « E » est le centre de …… et de ………..

Remarque : Une rotation de 180°  est aussi appelée « demi-tour ».