TRAVAUX AUTO FORMATIFS :   (le questionnaire reste à faire )

A)  LA SAISIE  de données : le sondage  et l’enquête.

La statistique est une science ancienne . Elle est utilisée de nos jours en médecine , science sociale et science de l’Education ,en psychologie , en fiscalité , en physique ; …..etc. et bien entendu en économie et notamment en gestion des entreprises.

Il est commun de dire que « gouverner et gérer c’est prévoir » , cela implique qu’avant de faire des prévisions, il est nécessaire de savoir. La statistique  permet d’avoir une meilleure connaissance des faits et habitus et de faciliter la prise de décisions. 

OBSERVATION : 

Les sources d’informations nécessaires pour faire l’étude statistique d’une population constituent des éléments de base fondamentaux .

Donc , la saisie de données  pour étude   s’effectue à partir de  deux types d’enquête :

L’enquête exhaustive ( recensement ) , et l’enquête partielle  ( sondage) ;

Enquête exhaustive .

On effectue une enquête exhaustive si on enregistre les renseignements concernant tous les membres d’une population. On dit aussi qu’on effectue un recensement : c’est le cas du recensement du nombre de naissances d’une ville pendant une période donnée. Ce procédé est très précis , simple et sûr .

L’ enquête partielle ( SONDAGE ):

Lorsque la population statistique est  trop nombreuse on étudie un sous ensemble  de la population , appelé « échantillon » , sur lequel on détermine l’observation des faits . Ce procédé est moins précis et la statistique mathématique cherche  dans quelles conditions on peut étendre  à la totalité de la population les résultats obtenus sur l’échantillon. On dit qu’on a procédé par « sondage »

C’est le cas des sondages d’opinion sur les intentions de vote .

        L’enquête par sondage  consiste à poser un certain nombre de questions à un certain  nombre de personnes.

 Pour recueillir les informations données par la personne interrogée , plusieurs moyens sont possibles :

-         les contacts  direct par enquêteur .

-         la voie postale .

-         le contact par téléphone .

Quel que soit le moyen utilisé  , une   attention  toute particulière à la rédaction du questionnaire .

B)  l' observation des faits ( exemple de dépouillement ).

ENREGISTREMENT DES OBSERVATIONS et Exploitation et dépouillement des données : 

Exploitation et dépouillement des données : 

:

Supposons  qu’on doive définir une statistique portant sur les notes  de cent élèves à la suite d’un examen ;Les notes figurent dans le tableau ci – dessous et ont été distribuées au fur et à mesure de la correction.

La liste de ces notes   attribuées à chaque élève s’appelle « série statistique »

Passage de l’enquête (inventaire ou recensement) au tableau :

Certaines caractéristiques apparaissent facilement : peu de notes inférieures à 3 et supérieures à 17 ,  il est difficile de tirer des indications générales de ces données présentées sans ordre . On commencera dons par « classer » suivant le tableau qui représente  le nombre d’élèves ( noté : n_i  ) ayant obtenu la note ( notée : x_i  )

Ce tableau présente l’inconvénient d’être volumineux .On peut choisir d’effectuer un regroupement des valeurs de la variable (note) suivant 5 classes .

Pour cela on partage l’intervalle [ 0 ; 20] en 5 intervalles partiels comprenant chacun 4 notes sauf le dernier qui en contient cinq .

On obtient les classes suivantes :

[  0 ; 4  [    groupant les  x_i   tels que      0  £  x_i  < 4

[  4 ; 8   [    groupant les  x_i   tels que       4  £  x_i  <  8

[  8 ; 12 [  groupant les  x_i   tels que       8  £  x_i  <  12

[  12  ; 16 [  groupant les  x_i   tels que    12  £  x_i  <  16

[  16  ; 20 ]  groupant les  x_i   tels que   16  £  x_i  £  20

 .Les valeurs  2 ; 6 ; 10 ; 14 ; 18 ,  sont appelées « valeurs centrales » des classes .

Dans ces conditions , le dépouillement se présente suivant le nouveau tableau suivant :

C ) CLASSE :  constitution  d’une classe , « classe modale », , « valeur centrale d’une classe », « classes et amplitude ».

  l'effectif total des éléments pris en compte sont regroupés par catégorie ou "classe".

                (les classes  (intervalles) sont imposées par le statisticien ) ; les classes n'ont pas obligatoirement la même amplitude ( existence des valeurs entre  les bornes peuvent être différentes ; mais attention , lors de la représentation graphique "histogramme" de respecter l'aire de référence .

Constitution d’une classe :

Lorsque les "caractères" sont mesurables  ; on organise les "réponses" en classe de nombres ,C'est à dire :

C.A.   en milliers d’euros )

x _i

Effectifs

(  n _i )

L’effectif «  n ₃ » de la classe «  x ₃ » étant le plus grand .

La classe « x ₃ »  est la classe « modale » ;

    x ₁ =300 à moins  500

22

    x ₂ = 500 à moins  800

25

    x ₃ = 800 à moins  1 000

 n _{3  =}  90

    x ₄ = 1 000 à moins 1400

33

    x ₅ = 1 400 à moins  1500

24

     x ₆ = 1500 et +

  6

Remarques :

► pour tracer le polygone des effectifs  ou fréquences, il faudra rechercher pour chaque classe observée : « son centre de classe » .appelé aussi : « moyenne de centre de classe » ou « valeur centrale d’une classe ».

► Dans le calcul de l’écart type  , on prendra la valeur centrale de chaque classe comme « x _i »

« valeur centrale » d’une classe.

exemple

C.A.   .(milliers d’euros )

x _i

C.A.   .(milliers d’euros )    x _i

Peut s’écrire

Centre de classe :  x _i

300 à moins  500

[ 300 ; 500[

500 à moins  800

[ 500 ; 800[

( 500 + 800) /2 = 650

800 à moins  1 000

[ 800 ; 1000[

(800 + 1000) / 2 = 900

1 000 à moins 1400

[ 1000 ; 1400[

( 1000 + 1400 ) /2 = 1200

1 400 à moins  1500

[ 1400 ; 1500[

(1400 + 1500) / 2 = 1450

1500 et +

????

Il faudra connaître le C.A. maxi

On se souviendra que dans les calculs de l’écart type on « admet que les valeurs observées sont celles du centre de la classe ».

« Classe » et « amplitude »

La représentation graphique des effectifs d’une variable continue ( organisation de « classe » pour ranger ces effectifs)peut s’effectuer sous la forme d’un histogramme.

Pour respecter le principe de construction de l’histogramme, on devra veiller à vérifier que les intervalles  de toutes les classes sont égaux.

, On dit que les clases doivent avoir la même amplitude.

Exemples :

Classes d’amplitudes inégales

Classe d’amplitudes égales

[ 300 ; 500[

Cette série ne sera pas exploitable pour tracer un histogramme. Il faudra repenser la distribution.    Voir « l’informaticien ».

[ 300 ; 500[

Cette série est exploitable pour tracer un histogramme.

[ 500 ; 800[

[ 500 ; 700[

[ 800 ; 1000[

[ 700 ; 900[

[ 1000 ; 1400[

[ 900 ; 1100[

[ 1400 ; 1500[

[ 1100 ; 1300[

????

[ 1300 ; 1500[

D) Statistique descriptive   et  l’ « événement » .

        Elle commence là où la donnée d'un tableau de nombres exprime des grandeurs liées au phénomène étudié : le nombre de naissances annuelles dans les dix dernières années , la répartition de ces naissances en sexes , la catégorie socioprofessionnelle des parents , etc ..

       On pourrait étudier un caractère de cette population dont les unités statistiques sont les nouveaux nés au cours de ces dix dernières années , par exemple le poids de ces nouveaux nés. A chaque nouveau né correspond un poids. Cela est un événement.

Autre exemple:

 Nous relevons les tailles en cm de 30 individus adultes , pris au hasard. A chaque  individu correspondra une taille.

        Je dispose d'une distribution de la taille en fonction des individus. Je peux dire que la taille varie en fonction des individus. La taille , cette caractéristique de chaque individu est une variable , et l' événement est ce couple taille-individu .

Après recensement des  variables , nous obtenons le tableau de données suivant:

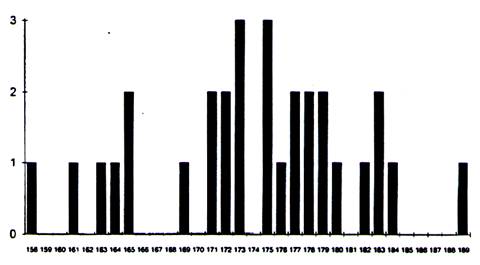
Nous constatons que certains événement se produisent 3 fois , deux fois , d'autres une fois et d'autres pas du tout .

 Nous pouvons également faire un tableau de la distribution des mesures. Nous pouvons  aussi   faire une représentation graphique , il s'agit là d’un diagramme en bâtons.

Nous pouvons prolonger notre analyse :

A partir de ce diagramme ,on pourrait dire que plusieurs groupes peuvent être repérés, celui des grands ,celui des petits et celui des moyens .Mais je peut être plus rigoureux en regroupant , en un certains nombre de classes les tailles des individus par exemple de 5 cm en 5 cm .J'aurai la classe des individus dont la taille et comprise entre 158 et 162 cm , puis celle des individus ayant entre 163 et 167 cm  , etc ; …nous obtenons le tableau suivant:

Nous « distribuons » des effectifs après regroupement des individus .que nous appellerons « classe ».

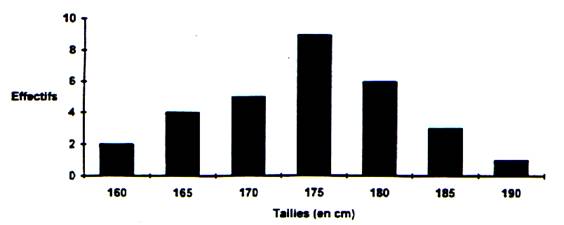
Commentaire :

En opérant le regroupement en intervalles , nous avons constitué 7 classes.

Dans chaque classe , les effectifs montrent le nombre d'événements produits  (l' événement est : taille - individu).

Si nous divisons par classe , la somme des  valeurs extrêmes  , nous trouvons une valeur que nous appelons «  valeur centrale »  .

Pour pouvons obtenir un autre diagramme « bâtons ».

Le choix des intervalles d'égale valeur sera effectué cas par cas en tenant compte de la précision recherchée ou demandée pour l' étude statistique , (et du coût projeté pour l'étude :il y a un organisme financeur de cette étude)

Un conseil  sur les bornes de chaque intervalle : il ne faut pas reprendre la valeur précédente dans la classe suivante ( 158-162 ; 163-167 ; 168  etc.…)

Pour l'étude des nouveaux nés , des intervalles de 150 en 150 g auraient convenu ,en supposant que les poids soient répartis entre 3,5 kg et 4,5kg  , nous aurions 7 « classes ». 

Les mesures sont des observations qui informent

Reprenons les tailles :

Commentaire :

En opérant le regroupement en intervalles , nous avons constitué 7 classes. Dans chaque classe , les effectifs montrent le nombre d'événements produits  (l' événement est : taille - individu).

Si nous divisons l'effectif de chaque classe par le nombre de mesures (30),      

nous obtenons la           " Fréquence" de chaque classe .

Si nous observons le résultat du  calcul de chaque classe, nous constatons que les 7 événements possibles n'ont pas la même fréquence.

Si nous faisons la somme des fréquences , nous obtenons "1 " : la somme des fréquences est l' événement certain : chaque individu a une mesure .

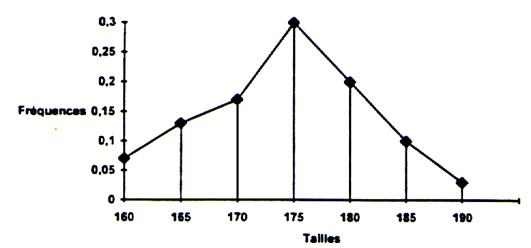
Un autre échantillon tiré de la même population "parente" aurait sensiblement la même distribution. On peut estimer que la distribution des fréquences dans la population parente aurait la forme théorique présentée ci-dessous.

Courbe des fréquences

Il y a les données de rang :      Il y a deux cas :

Ou bien les données sont collectées en termes de rang ,

ou bien les données  collectées n'atteignent  pas le niveau de l'échelle d'intervalle , elles peuvent être remplacées par leurs rangs si l'on peut vérifier qu'elles atteignent  ce niveau de mesure .

exemple :  une course d'éducation sportive : l'histogramme est plat ;chaque élément occupe un rang .

Résumé des observations :

Nous remarquons que les observations recueillies nous permettent de repérer deux catégories d'indices pour décrire nos ensembles de données. (nous ne  nous situons que  par rapport aux données de score)

Cliquer ici pour plus d'informations sur ces indices :

Suite : les indice de position et de dispersion :

A )  Les indices de position

Voir les travaux auto formatifs.

B)  Les indices de dispersion