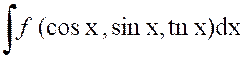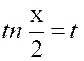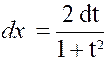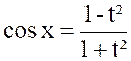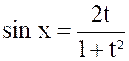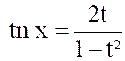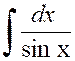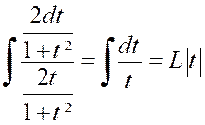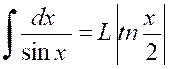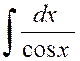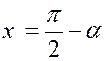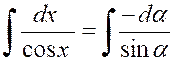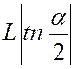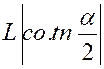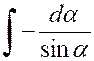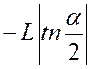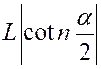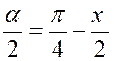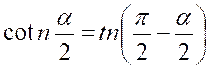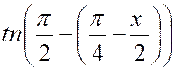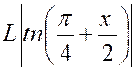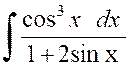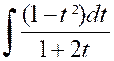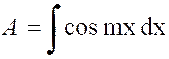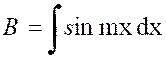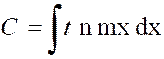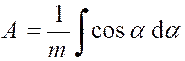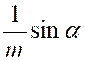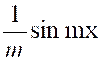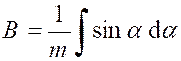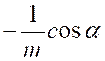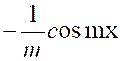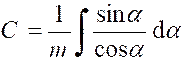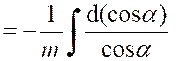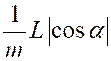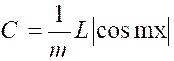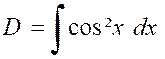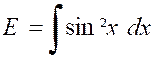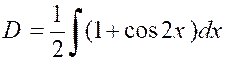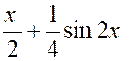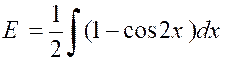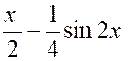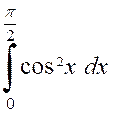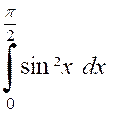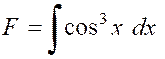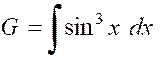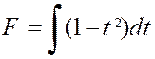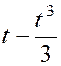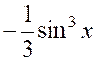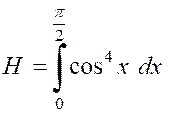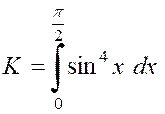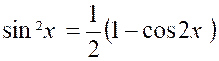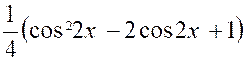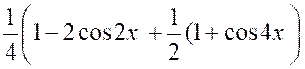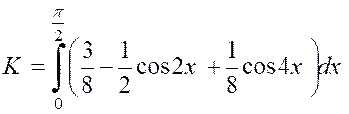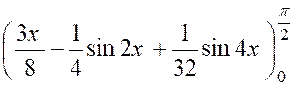COURS

Soit l’intégrale :  

Ou «  » est une fonction rationnelle des lignes de l’angle «  ».

On peut toujours se ramener à une intégrale rationnelle en faisant le changement de variable «   »

D’où  «  » ;           «  »

Mais cette méthode est longue et on doit , autant que possible l’éviter.

Exemple 1 .  calculer :

Le changement de variable précédent donne

Exemple 2 : 

Au lieu de calculer directement cette intégrale par le même changement de variable , ramenons – nous à l’intégrale précédente en posant :

On a alors « dx = - d », et par suite :

=  = 

or

= =  =

or

  et   .=

Finalement : =

On peut souvent simplifier le calcul d’une intégrale trigonométrique en appliquant la règle suivante :

·       Si l’intégrale ne change pas quand on remplace « » par «  » on peut prendre comme variable «  »

·       Si rien n’est changé quand on remplace «  » par  «  » on prend pour variable «  » ;

·       si on remplace  « » par  «  » on prend comme variable «  »

Ceci se retient facilement, car ce sont précisément ces changements qui n’altèrent pas les lignes correspondantes.

On a en effet :

«   »

«  »

«  »

E

xemple : calculons : 

Si on remplace « x » par «  » , « sin x » n’est pas changé , « cos ³ x » est changé de signe, « dx » aussi , de sorte que le produit « cos ³ x   dx»  On peut donc poser « sin x = t » , d’ où « cos  x   dx = dt » ; « cos ² x  = 1 – t ² », et on se ramène ainsi à l’intégrale rationnelle :

Quelques intégrales trigonométriques courantes :

Soient d’abord les trois intégrales

Posons : «   »     d’où  «   »

On obtient ainsi :

 ;                                         =              = 

 ;                                             =              = 

   ;                   ;                             =    

ou encore :

Soient encore deux intégrales (avec des « carrées »

Et

Pour calculer ces deux intégrales nous exprimerons « cos² x »  et « sin² x » en fonction de « cos 2x » , à l’aide des formules :

·       «  2 cos ² x = 1 + cos 2x »

·       « 2 sin² x = 1  - cos 2x  »

Nous obtenons :

  devient      = 

  devient      = 

En particulier :

         =               = 

Soient encore deux intégrales (avec des « cubes »)

Elles s’obtiennent facilement en opérant  un changement de variable.

Pour calculer « F » , par exemple, nous posons  « sin x = t » , d’où « cos x dx = dt »  et  « cos ² x = 1 – t ² »

D’où :

  =   =   sin x

Soient encore deux intégrales (avec des « puissances quatrièmes »)

                  et                              

Pour calculer « K » , par exemple, exprimons «  sin ⁴ x en fonction linéaire des lignes de l’angle « »  et de ses multiples.

On a d’abord

Puis : «  sin ⁴ x =    = 

Par suite :

  =   =

CE qui termine  ce cours…………..

TRAVAUX AUTO FORMATIFS.

CONTRÔLE

Voir le cours !!!!!

EVALUATION :

calculer :

=

=

Voir le cours !!!!!