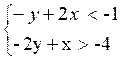Pré requis:

Régionnement et inégalité des distances (5ème)
Système d’équation du premier degré à une inconnue
Résolution de l’équation du premier degré à deux inconnues
Fonction linéaire (représentation graphique)
Fonction affine (représentation graphique)

ENVIRONNEMENT du dossier:

Index warmaths

Objectif précédent : 1°) Egalité degré 1 à une inconnue . 2°) Premier degré à deux inconnues et régionnement. 3°) Liste des cours sur les inéquations…

Objectif suivant : 1°) Système de deux équations du premier degré à 2 inconnues. 2°) système d’inéquations du premier degré à deux inconnues.

1°) Résolution de systèmes d’équations du premier degré à deux inconnues 2°) liste des cours de bases sur les systèmes d’équations du premier degré à deux inconnues.

DOSSIER : SYSTEMES DE DEUX EQUATIONS du PREMIER DEGRE à deux INCONNUES .

(cours n°2 :Généralités)

· GENERALITES

· LES METHODES de RESOLUTIONS .

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité Ici >>> Fiches de travail

Corrigé Contrôle

Corrigé évaluation

COURS

Définitions .

Considérons deux équation du premier degré à deux inconnues :

(1) a x + b y + c = 0

(2) a’ x + b’ y + c’ = 0

Chacune de ces équations prise séparément admet une infinité de solutions.

Nous nous proposons de voir s’il existe des valeurs qui  , mises à la place de « x » et de « y » satisfont « à la fois » à ces deux équations. Si de telles valeurs existent , nous dirons qu’elles constituent une solution du système formé par les équations (1) et (2). Donc :

1°) On appelle « système » de deux équations du premier degré à deux inconnues l’ensemble de deux équations du premier degré à deux inconnues.

C’est donc un système de la forme :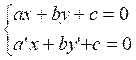

Dans lequel « x » et « y » sont les inconnues et « a ;b ;c ;a’ :b’ ;c’ » sont des données.

On dit que deux systèmes sont équivalents lorsqu’ils admettent les mêmes solutions.

2°) On appelle « solution » de ce système tout ensemble de deux nombres qui , mis à la place de « x » et « y », satisfait à la fois aux deux équations de ce système.

Résoudre un système de deux équations à deux inconnues , c’est trouver ses solutions.

PROPRIETES : les propriétés suivantes sont évidentes.

1°) Pour résoudre un système d’équations on peut remplacer les différents membres de chaque équation par des expressions équivalentes.

Ainsi pour résoudre le système :

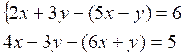on peut l’écrire :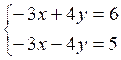

On peut remplacer u ne équation par une équation équivalente.

Ainsi résoudre le système :

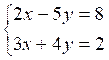on peut l’écrire :

>>>> Voir plus d’informations ;

TRAVAUX AUTO FORMATIFS.

CONTROLE :

1°) qu’ appelle t - on « système » de deux équations du premier degré à deux inconnues ?.

2°) soit le système de la forme :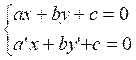

qu’appelle - t -on ? x ; y et « a ;b ;c ;a’ :b’ ;c’ ».

3°) Quand dit -on que deux systèmes sont équivalents ?

4°) qu’appelle t- on « solution » d’un système.

5°) Résoudre un système de deux équations à deux inconnues , cela consiste à quoi faire ?

EVALUATION

A)

Résoudre graphiquement les inégalités suivantes :
x - 2y + 4 > 0	(corrigé dans le cours)
y – 3 > x -5
2x – 5 > x + 4
2y -< x +
- 4y + > x + 4

B) Résoudre le système suivant :

Corrigé dans le cours.