|
SOMMAIRE : 5 / 25
LIVRE Niveau V. MODULE
: LES RATIONNELS |
|
|
L’ étude de ce
module , sur les rationnels , se décompose en 5 cours . |
|
INFORMATIONS PEDAGOGIQUES :
|
|
OBJECTIFS : - Savoir
faire des calculs avec des fractions de mêmes dénominateurs « Addition » ;
« soustraction » ; « multiplication » ;
« division ». - Savoir
faire des calculs avec des fractions de dénominateurs différents
« Addition » ; « soustraction » ;
« multiplication » ; « division ». - Savoir
faire des calculs avec une fraction et un nombre . .
« Addition » ; « soustraction » ;
« multiplication » ; « division ». |
Important :
Pour faciliter les calculs et
pour éviter les risques d’erreurs de calcul , il est
conseillé de
simplifier jusqu’à rendre irréductible la ou les
fractions .
|
|
|
|
|
|
|
|
A) SOMMAIRE @ : tout sur ce qu’il faudrait savoir sur « la
fraction ». B) Sommaire sur : l’Addition @ calculs se ramenant à l’addition de deux fractions. C) Sommaire sur @
calculs se ramenant à la soustraction
de deux fractions. D) Sommaire sur @
calculs se ramenant à la multiplication
de deux fractions. E) Sommaire sur
@ calculs se ramenant à la division de deux fractions. |
|||||
Définitions
préalables
« Fraction » : La fraction est le rapport (une division ) d’un
nombre entier naturel par un autre nombre entier naturel
Exemple : 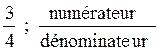
« Rationnel » Un rationnel
est le quotient d’un entier par un entier « non nul ». ( on dit aussi : « différent de
zéro » ; noté : ¹ 0 )
Exemples : 16
: 2 = 9 9 est un rationnel
25:
4 = 6,25 6,25 est un rationnel
11
: 7 =
11/7 11/ 7 est un
rationnel
« Ecriture fractionnaire » : On
appelle « écriture fractionnaire « une fraction possédant, au moins
un nombre décimal ».( Il y a au moins un nombre
décimal au numérateur ou au dénominateur.)
Pour des raisons
« pratiques » il est souvent
demandé d'exprimer le résultat du
calcul sous une forme qui vous est
précisée: exemple :« arrondi à
…0,001… » ( pour
plus d’information consulter le
CD : les « nombres irrationnels » @