|
|
CORRIGE TRAVAUX SOMMATIF B. E . P. |
Pour aller
directement aux informations « cours » voir cas
par cas. |
||
|
Devoir N° 2 /
15 |
Matière : MATHEMATIQUES |
|||
|
|
|
|||
|
|
||||
|
OBJECTIFS : Travaux BILAN de fin de
formation en vu d’obtenir une
validation de la formation . Peut être utilisé pour faire un
diagnostique. |
||||
|
|
||
|
|
|
|
|
|
TRAVAUX CONTROLE |
|
|
|
|
|
|
|
Les questions relatives à
« ce qu’il faut retenir » , au
« savoir » se reporter aux cours . |
|
|
|
|
|
|
|
TRAVAUX :
EVALUATION |
|
|
|
1. |
Caroline
dépense 30 € pour acheter 5 CD
et 6 cassettes audio . Il faudrait
4 € de plus pour acheter 8 CD
et 4 cassettes. Trouver le prix d’un CD et
celui d’une cassette . 1°) Calcul de la valeur d’un CD : Soit le système : 30 = 5 CD + 6 C 34 = 8
CD + 4 C Soit le second système : on va
éliminer les « C » , on trouve 12 comme plus petit multiple
commun ! On multiplie par - 2
: -60 = - 10 CD - 12 C On multiplie par 3
: 102 = 24 CD + 12 C on additionne : 42 = 14 CD ; un CD = 3 Calcul de la valeur d’une
cassette : 30 = 15 + 6C donc
15 = 6C ; C = 15 / 6 ; C = 2,5 Conclusion : un CD = 3 € et une cassette = 2,5 € |
|
|
|
|
|
||
|
2. |
|
|
|
|
|
Joindre les calculs si
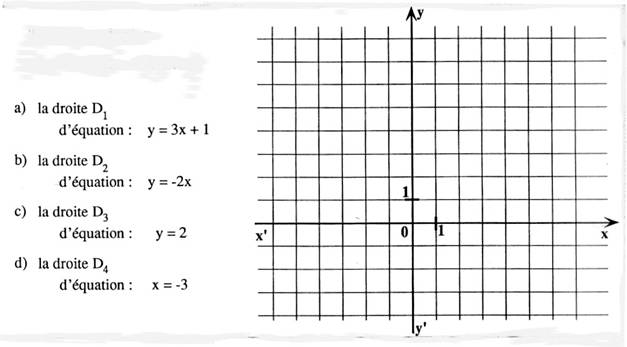
nécessaire. ►La droite D 1
est la représentante de la fonction affine. Avec « x = 0 ; y =
1 » et si « x =
2 ; y = 7» ►La droite D2
est la représentante de la
fonction linéaire . Avec « x = 0 ; y = 0 »
et « x= 2 ; y = - 4 » ►la droite D3 est une droite parallèle à l’axe des « x »
et passant par le point y = 2 ► la droite D4 est une droite parallèle à l’axe des
« y » et passant par le point x = -3 |
|
|
|
|
|
||
|
3. |
Un article valait 2560 € en 1999 ,
il vaut 2880 € en 2003 Calculer l’indice du prix en
2003 ; base 100 en 1999. |
|
|
|
|
Réponse : |
|
|
|
|
|
||
|
4 |
|
|
|
|
|
Nous ne devons donner que
des valeurs approchées : Sur les angles :
c’est une indication. Les valeurs recherchées
en valeurs approchées , acceptées sont : Afrique :180 + ou - « 2 millions » Asie : 120 + ou - « 2 millions » Amérique : 420 + ou - « 2 millions » |
|
|
|
5. |
En utilisant les identités
remarquables , SOS Cours. |
|
|
|
|
Sans la calculatrice et sans poser
la multiplication : calculer ( 299 995 ) ² Utiliser la
formule : ( a - b ) ² = a² - 2 ab + b² Donc 299 995 = 300 000 - 5 ; on calcule ( 300 000 - 5 ) ² = 9 0 000 000 000 + 25 -
3 000 000 = 89 997 000 025 |
|
|
|
|
|
||
|
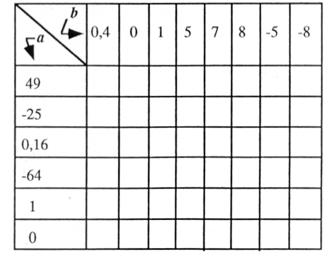
6. |
Parmi les nombres « a » de
la liste verticale, certains admettent
une racine carrée , d’autres non. Les nombres « b »
de la liste horizontale représentent
des réponses possibles . Cocher d ‘une croix les cases qui associent
un nombre « a » avec sa racine « b » » ; ( b = |
|
|
|
|
|
|
|
|
Fin du devoir 2 / 15 |
|||
|
|
0,4 |
0 |
1 |
5 |
7 |
8 |
-5 |
-8 |
|
49 |
|
|
|
|
x |
|
|
|
|
-25 |
Rien : impossible |
|||||||
|
0,16 |
x |
|
|
|
|
|
|
|
|
- 64 |
Rien : impossible |
|||||||
|
1 |
|
|
x |
|
|
|
|
|
|
0 |
|
x |
|
|
|
|
|
|