Module : Les entiers.					DOSSIER : 34 et 35
LOGICIEL warmaths  ; Pour Aide et Formation Individualisée ; REMEDIATION mise à /NIVEAU : niveau VI _ niveau V
Info conseils et consignes.				TRAVAUX NORMATIFS niveau 6 et niveau 5 Mathématiques .			.>>>> leçon complémentaire : « échelle »
LES GRAPHIQUES : lectures et constructions.
INFO COURS :
@Info cours :les graphiques. 2°) les segments et « opérations »
TRAVAUX CONTROLE
Doc WR
TRAVAUX : EVALUATION
	Les graphiques sont des dessins qui représentent des grandeurs. Exemple : Julien a 8 ans; Paul a 10 ans. Si je représente 1 an par un trait d’un cm, je peux dessiner les âges, et les comparer facilement.
	Paul :
	Julien
	1.Dites, en regardant le graphique ci-dessus, qui est le plus jeune, qui est le plus vieux, et de combien d’années.
	2. En examinant le graphique ci-dessous où les années sont représentées par 1 cm, dites : a) l’âge de Louise, de Marie et de Jeanne; b) la différence d’âge entre Louise et Marie (………..) , Marie et Jeanne (………) , Louise et Jeanne ( ………).
	Louise
	Marie
	Jeanne
	3. A raison de 1cm pour 1 an, représentez graphiquement les âges de Paul (5 ans), Michel (7 ans), Momo (10 ans), Lucile (11 ans) et, en regardant le graphique, dites la différence d’âge entre Paul et Michel; Paul et Momo; Paul et Lucie; Michel et Momo; Michel et Lucie; Momo et Lucile.
	4.Dans le graphique ci-dessous, chaque tête représente 1 million d’animaux;
	a) De combien de millions de bêtes a varié chaque élevage entre 1900 et 1950? Dans quel sens? (augmentation ou diminution?) b) Quel était le nombre total d’animaux élevés en 1900? en 1950? Comment ce nombre a-t-il varié? Vérifiez à l’aide des résultats de la question « a) » .
	5. A l’aide des données ci-dessus,faites le graphique linéaire en représentant 1 million de bêtes par un segment de 5 mm de longueur.
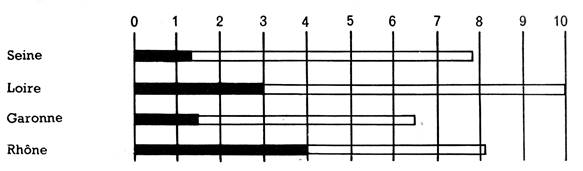
	6. Quel est le fleuve au plus long.
	Voici, représentées à raison de 1 cm pour 100 km 1 min pour 10 km), les longueurs des 4 grands fleuves français (en noir le cours au-dessus de 200 m d’altitude; en clair, le cours en plaine) 1 graduation = 1 centaine de km
	Quel est le fleuve le plus long? le plus court? Classez les 4 fleuves du plus court :
	7. D’après l’échelle graphique, indiquez approximativement la longueur de chaque fleuve. :
	8. Sur le graphique, 1 mm représente 10 km. Mesurez, en millimètres, la longueur de chaque représentation de fleuve. Calculez la longueur réelle de chaque fleuve, à 10 km près. Comparez vos résultats avec ceux de votre lecture approximative (n° 2). 9. Évaluez, puis mesurez la longueur du cours de chaque fleuve au-dessus de 200 m d’altitude; exprimez-la en kilomètres. 10. Évaluez, puis mesurez la longueur du cours de chaque fleuve en plaine (moins de 200 m d’altitude); exprimez-la en kilomètres. 11 .Reproduisez, dans votre classeur , à la même échelle, le graphique ci-dessus.
	12. Par un petit trait vertical, figurez sur chaque ligne du graphique, en partant de 0, l’emplacement des villes suivantes (la distance est indiquée à partir de la source) Seine Troyes 190 km ; Montereau 310 km; Paris 420 km. Loire Roanne 280 km; Nevers 460 km ; Orléans 630 km. Garonne Toulouse 220 km; Agen : 350 km; Bordeaux 580 km. Rhône Genève 220 km; Lyon 450 km; Avignon 750 km. Évaluez ensuite, puis mesurez les distances de ces villes à la mer, par le fleuve sur lequel elles sont situées.
	13. En prenant 2 mm pour 100 km, représentez graphiquement la longueur des fleuves suivants : Loire : 1 000 km; Volga : 3 400 km; Amazone 6 000 km; Nil : 6 500 km.