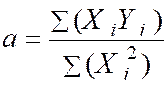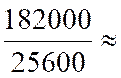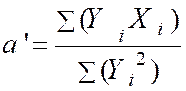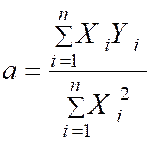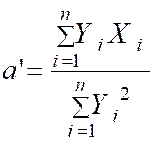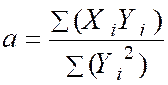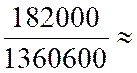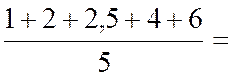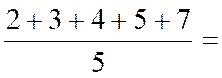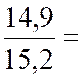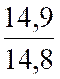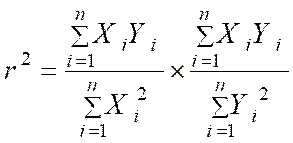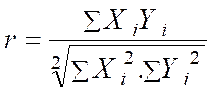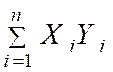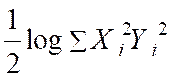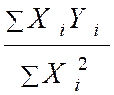COURS

Ce qu’est la corrélation (explications)  :

Afin d’anticiper les événements et pour faciliter certaines prises de décision , les responsables d’entreprise essayent de déterminer des « indices annonciateurs » du futur .

Cette recherche de liaisons entre les phénomènes peut être plus ou moins « quantifier ».

Prenons par exemple ( n°1)  Dans  une entreprise , son expérience montre que le chiffres d’affaires de l’automne d’une année indique avec une certaine fiabilité celui du printemps suivant. et ce , malgré une absence apparente de « causes » entre les deux phénomènes  (automne et printemps).

Ce que l’on appelle ici « expérience » n’est en fait que la forme « subjective » d’un repérage de liens (liaisons) entre les deux phénomènes.

Cependant

Cette façon de voir , très élémentaire et restrictive , des liaisons n’indique pas ou mal la durée et l’intensité de ces liaisons. Il est donc nécessaire de les quantifier.

Le chapitre des statistiques qui permet de répondre à ce besoin en « mesurant » l’intensité de la relation existant  entre deux phénomènes est appelée : la corrélation.

Cette approche rationnelle qu’est la corrélation s’est inspirée de celle des sciences dites fondamentales ( par exemple : la physique) qui sont par définition « causalistes » et « réversibles » .

Prenons par exemple (n° 2) : une augmentation déterminée de température dilate de façon constante le mercure dans le tube du thermomètre,et inversement une dilatation donnée de ce métal indique une augmentation « connue » et « constante » de température.

Le monde économique de la gestion n’est pas aussi « exact et parfait » et les liaisons  entre phénomènes ( quand ils existent ) ne  sont  pas souvent  ( voir :rarement ) réversibles et constantes

Revenons sur l’exemple n°1 : Il se peut que les  ventes de l’automne de l’année « n » ,indiquent celles du printemps de l’année suivante  , mais il n’y a aucune raison que ces dernières nous permettent de prévoir celles de l’automne   ( n +1).

Enfin, l’existence de corrélation entre deux phénomènes n’indique pas obligatoirement une relation causale  entre ces deux phénomènes. ( Le chiffre d’affaires du printemps  de l’année « n +1 » ne représente pas la cause du chiffre d’affaires du printemps suivant , il n’en est seulement  qu’ un indicateur . 

En fait , le lien de corrélation entre deux phénomènes est un lien intermédiaire entre :

-          la liaison fonctionnelle que l’on note  «  y =  f (x ) » : par exemple , la circonférence d’un cercle ( notée : « y ») est fonction ( f  ) de la grandeur de son rayon ( noté : x )

-          et de l’indépendance totale. Par exemple , l’évolution du prix du gazole  et celle des cotisations sociales.

C’est ce qui explique que la méthode de la corrélation se ramène au calcul d’une liaison fonctionnelle à une approximation prés.

C’est la démarche du développement qui suit :

1°) Les droites de régressions.

2°° Le coefficient de corrélation.

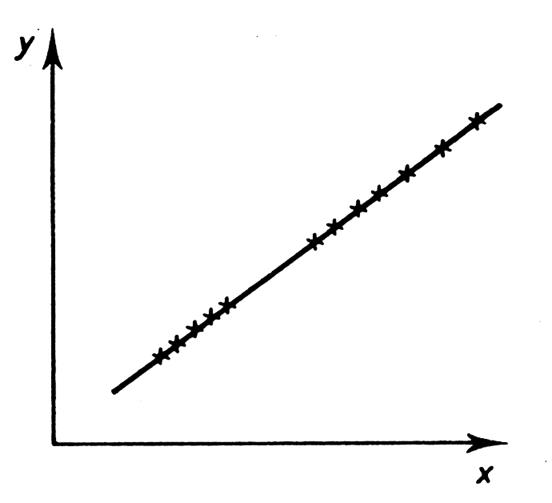
Au préalable  il faut s’efforcer de « repérer » les relations existantes entre deux phénomènes  représentés  par un nuage de points.

Nous allons voir r plusieurs « nuages de points » possibles  qui sont les caractéristiques de différentes corrélations.

I )  Les nuages de points :

Il s’agit , nous l’avons vu dans le cours sur les ajustement s,  des représentations graphiques des différents couples de deux caractères ( 2 variables) . Ils permettent de visualiser , globalement, le lien de dépendance statistique. Ce dernier, quand il existe, peut être linéaire ou pas.

Dépendance linéaire parfaite

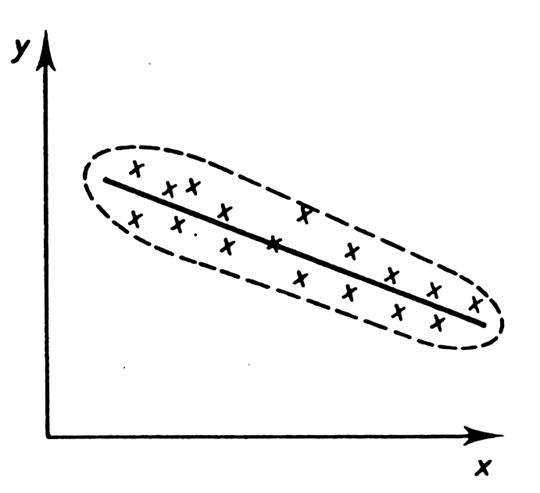
Dépendance linéaire forte

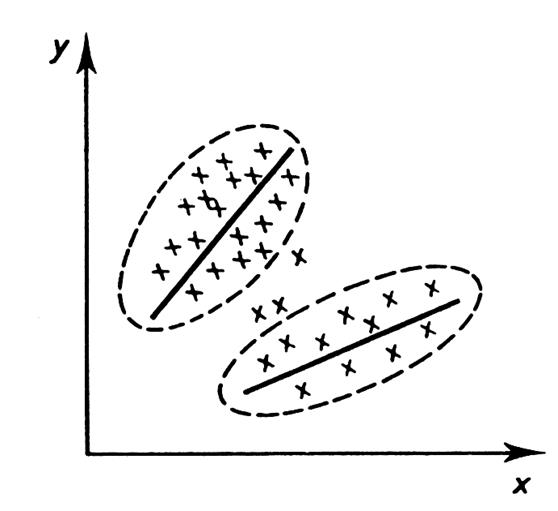
Dépendance linéaire double

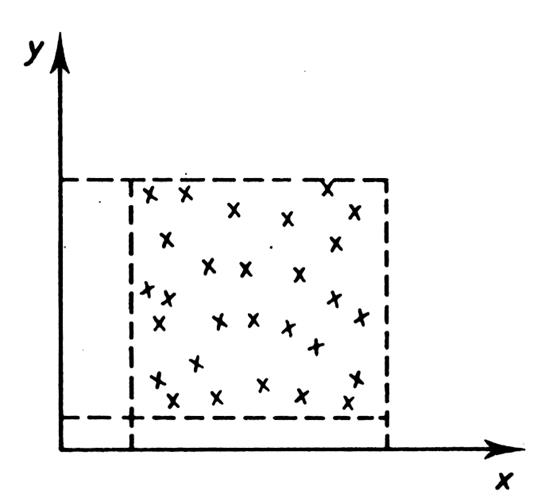
Indépendance

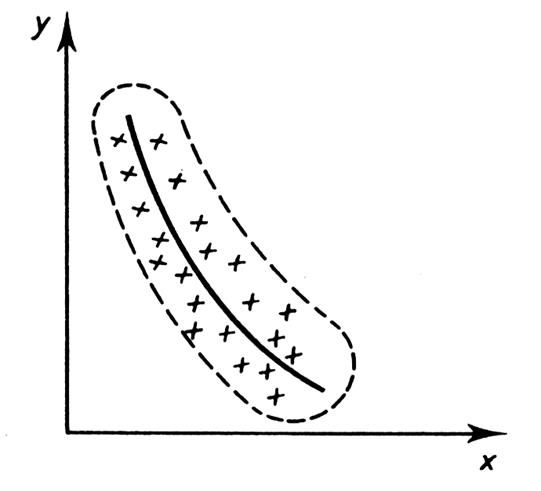
Dépendance non linéaire (hyperbolique)

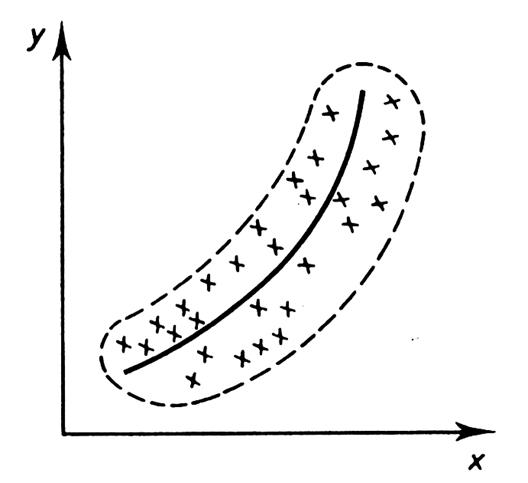
Dépendance non linéaire (exponentielle )

II ) Les droites de régression.

Nota : attention , dans tout ce qui suit l’existence d’une relation linéaire ne signifie pas « lien de cause à effet ».

La mesure de la corrélation est purement mathématique et peut être  effectuée entre des phénomènes indépendants. Il faudra donc toujours expliquer le pourquoi d’une forte corrélation (voir le nuage type  ci-dessus).

Dans le cas de séries à deux variables  ( x et y ) , il est possible de considérer successivement chaque variable comme variable expliquée , puis comme variable explicative (1) . Dans ces conditions, nous pourrons calculer deux droites de régression..

a)    La droite de régression de « y » en « x » d’équation «  y = a x + b » , permettant de déterminer « y » connaissant « x ».

b)    La droite de régression de « x » en « y » d’équation « x = a ‘ y + b ‘ » , permettant  ( 1 )de déterminer « x » connaissant « y »  

(1) dans le cas de séries chronologiques ( où « x » représente le temps) , la droite de régression de « x » en « y » n’a aucune signification.

Par exemple, une entreprise peut souhaiter expliquer et prévoir ses ventes ( y) par rapport à ces dépenses en publicité  en gagées ( x) ou , au contraire, déterminer ses dépenses de publicité «  y » en fonction de ses ventes (x).

Pour concrétiser ces notions, utilisons , pour la suite de l’exposé, l’exemple simplifié suivant .

Dépenses de publicité

Ventes

800

1 500

870

1 900

900

2 000

920

2 300

970

2 500

1 000

3 000

1°) Détermination de l’équation de la droite de régression de « y » en « x »,

a)     Choix des variables :

Nous sommes dans la situation suivante : le chef d’entreprise désire prévoir ses ventes ( « y » variable expliquée) par rapport à des dépenses de publicité engagées ( « x » variable explicative )

b)     Recherche des caractéristiques de la droite « y = a x + b »

L’équation de cette droite se détermine aisément en appliquant la méthode des moindre carrés . ( voir cours)

Rappelons que cette droite passe par le point moyen (  ; ) du nuage de points et que la valeur de la pente se détermine par le calcul en utilisant la formule suivante :

Avec :

X i = x i –

Yi = y i -

c ) application.

- coordonnées du  point moyen :    = 910   ;   = 2 200

- calcul de la valeur du coefficient  « a » :   =   7,11

-          calcul de la valeur  de  « b » :

«  b =   - a  »  =    2 200 – 6 470 = ( - 4270)

- Conclusion : l’équation de la droite de régression de « y » en « x » est : 

y = 7 ,11 x - 4270

2°) Détermination de l’équation de la droite de régression de « x » en « y »,

a) Choix des variables :

Nous sommes dans la situation suivante : le chef d’entreprise déterminer ses dépenses de publicité  ( qui deviennent  des variables expliquées « y » ) en fonction de ses ventes  « x » ( qui deviennent des variables « explicatives »).

b) Recherche des caractéristiques de la droite « x = a’ y + b’ »

L’équation de cette droite se détermine aisément en appliquant la méthode des moindre carrés . ( voir cours)

Rappelons que cette droite passe par le point moyen (  ; ) du nuage de points et que la valeur de la pente ( a ‘ ) se détermine par le calcul en utilisant la formule suivante :

Info : nous remarquons qu’en inversant les coordonnées la formule se détermine facilement à partir de la droite de régression de « y » en « x ». En effet, pour cette dernière :

  en remplaçant     X _i  par Y _i  et réciproquement  on a

c ) application.

      - coordonnées du  point moyen :    =2200   ;   = 910

-          calcul de la valeur du coefficient  « a » :   =   0,13

-          calcul de la valeur  de  « b » :

«  b’ =   - a ‘   »  =    910  – (2200  x  0,13 = ( + 617,4 )

- Conclusion : l’équation de la droite de régression de « x » en « y » est : 

y = 0,13 x + 617,4

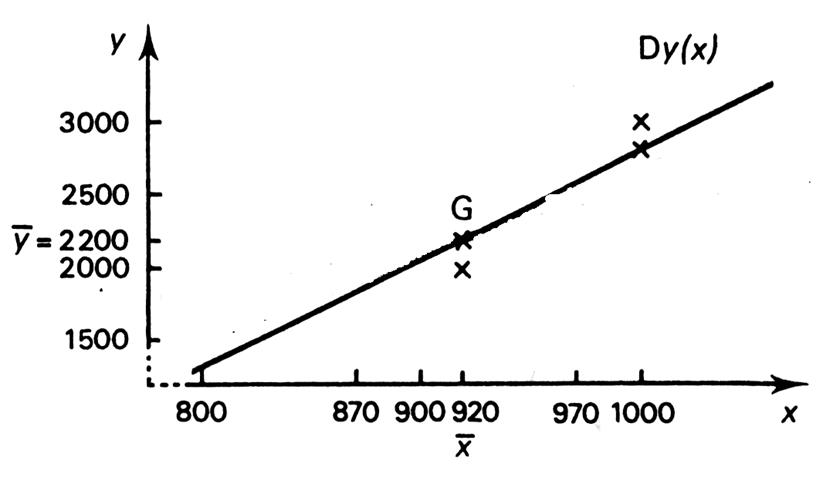
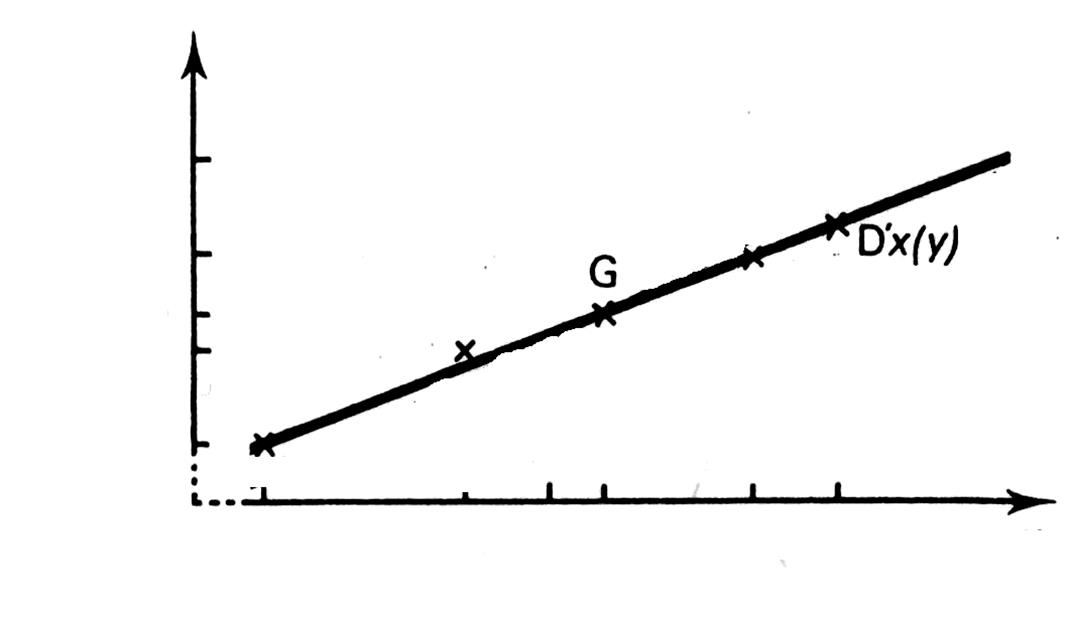
Modèle de la droite :  D’ x ( y )

3°)  Synthèses « graphique ».

Nous rappelons que pour la droite de régression de « x » en « y » ( D’  x ( y ) ) les coordonnées sont inversés.

Commentaire :

Il existe donc une liaison certaine entre les deux phénomènes .

Certes les dépenses de publicité expliquent « correctement » les ventes, mais ces dernières influencent certainement les dépenses  de publicité futures qui , à leur tour , conditionnent les ventes, etc.

En généralisant :

-          La droite de régression de « y » en « x » :  D  y ( x )

-          La droite de régression de « x »  en « y » :  D’ x ( y )   

4°) Conséquences .

a)     Le dénominateur de « a » est le carré de l’écart type de la série des «  x _i »  ( soit sa « variance ») . De même pour «  a ‘ » le dénominateur représente la « variance » de la « y _i ».

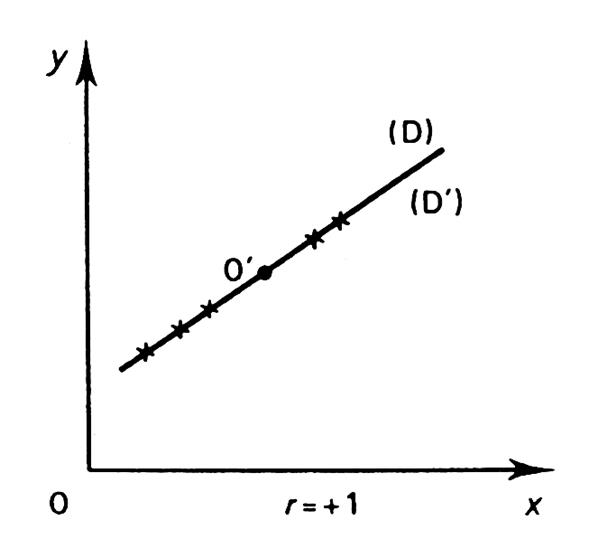
b)     Les deux droites de régression ont des coefficients directeurs ( « a » et « a’ ») de même signe. En effet , les dénominateurs de ceux-ci sont toujours positifs et leurs numérateurs sont identiques.

c)      Les deux droites de régression ( D et D’ ) ne sont confondues que dans le cas où :

«  a =       a a’ = 1

En effet :

«   »

« x = a’ y   y =   x »

 d ) Les numérateurs de « a » et « a ‘ » sont égaux . Leur valeur commune ( ) s’appelle « covariance » de la série statistique.

5° ) Application globale.

Semestre

Chiffre d’affaires

En dizaine de mille euros. ( y _i )

Charges d’exploitation

En dizaine de mille euros. ( x _i )

( 2 dizaines de mille = 20 000)

1

2

1

2

3

2

3

4

2,5

4

5

4

5

7

6

Calcul des coordonnées du point moyen.

·      Calcul de  : 4,2   ( soit 42 000 € )

·      Calcul de : 3,1   ( soit 31 000 € )

·      D’où on établit le tableau suivant

Chiffre d’affaires

( y _i )

Charges ;

( x _i )

Y _i =  y _i -

X _i =  x _i -

Y _i X _i

X _i ²

Y _i²

2

1

2  - 4,2 = - 2,2

1 – 3,1 = - 2,1 

( -2,2)(-2,1)= 4,62

( -2,1)² = 4,41

( - 2,2 ) ² = 4 ,84

3

2

3 – 4,,2 = - 1,2

2 – 3,1 = - 1,1 

1,32

1,21

1,44

4

2,5

- 0 ,2

- 0,6

0,12

0,36

0,04

5

4

0,8

0,9

0,72

0,81

0,64

7

6

2,8

2,9

8,12

8,41

7,84

21

15,5

14,9

15,2

14,8

Calculs des droites de régression « D »  et D’ »

·      Point moyen :   Ces droites de régression passent par le point moyen (centre de gravité) du nuage ( = 42 000    ;  = 31 000) ;

Elles ont pour équations :

·      D  y ( x ) est de la forme « y = ax + b »

Avec  «  a = ( Somme des Y _i X _i )   /  ( somme X _i ² » )  =     a =  0,98

                         Et  «  b = y – a x »

Au point moyen ( centre de gravité : barycentre » ) «  b =  - a  ; soit   =  42 000 – ( 0,ç_ x 31 000) =   11 620

Donc  L’équation de la droite «  D  y ( x) » 

y = 0,98 x + 11 620

·      D ’  y ( x ) est de la forme « y = a ‘ x + b’  »

Avec  «  a ‘   = ( Somme des Y _i X _i )   /  ( somme Y _i² » )  =     ;  a =  1 , 006

Détermination de « b ‘ » :   « b ‘ =   -  a ‘ » 

Soit au point moyen( G ) :  31 000 -  ( 42 000 x 1,006)  =  - 11 252

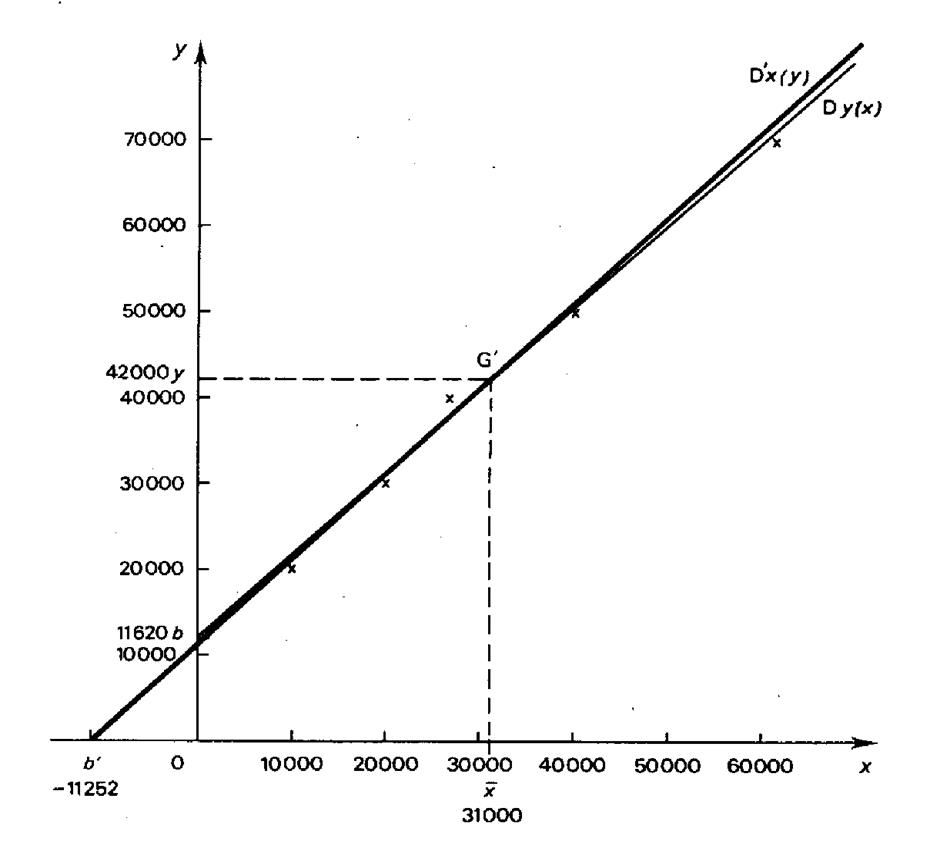
D’ où l’équation de la droite   D’ x ( y )  :    

x =  1, 006 y – 11 252

( rappel : dans les calculs précédents « x » et « y » sont exprimés en euros )

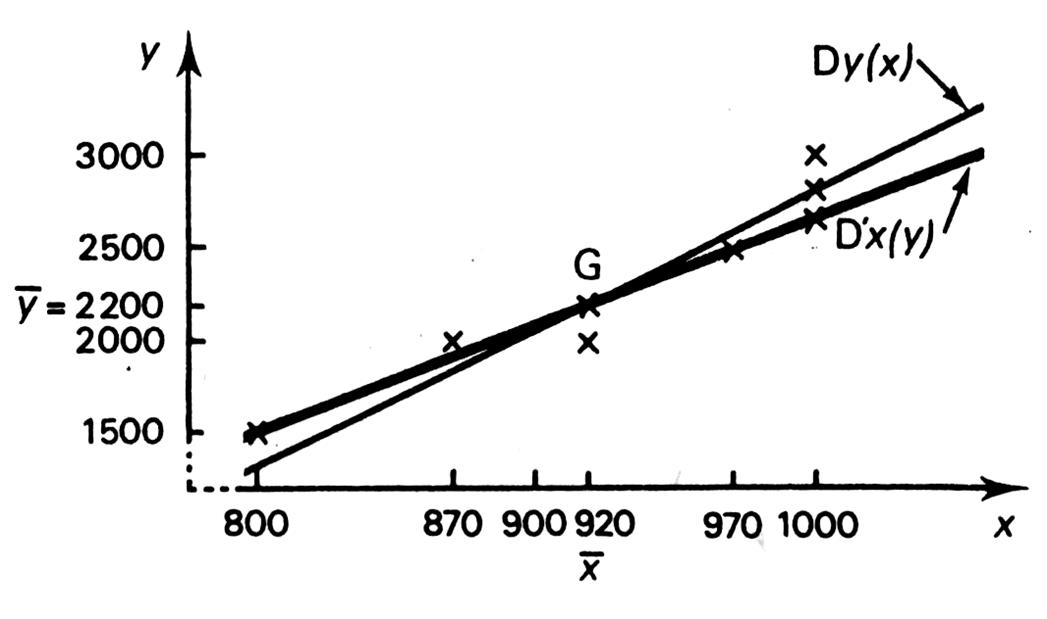
·      Représentation graphique

Remarque : Plus les points du nuage sont alignés ,plus les droites de régression sont proche l’une de l’ autre. Dit autrement  , plus la dépendance entre les deux variables étudiées est vérifiée, plus les deux droites sont proches l’une de l’autre.
Inversement, quand les deux caractères ( phénomènes) sont indépendants , les deux droites de régression sont  perpendiculaires .  

III ) Le coefficient de corrélation.

1°) Définition.

Le coefficient de corrélation « r » est un indicateur de dépendance entre deux phénomènes . Ce concept est très utile dans la gestion  et l’administration des entreprises. Il permet d’ « entrevoir » , puis de vérifier, l’existence d’un lien entre des phénomènes tels que les salaires et les prix, l’absentéisme et le taux des primes , les accidents du travail et les heures supplémentaires, etc.

De façon graphique , le coefficient de corrélation indique le plus ou moins grand degré de rapprochement des deux droites de régression.

Il se définit comme étant égal à la racine carrée du produit de la pente des deux droites de régression :

«  r ² = a . a’ »

r =

Remarques :

Le coefficient de corrélation :

-          est un nombre sans dimension compris entre 0  et

-          est toujours du signe de «  » , qui peut être « négatif » , « positif » ou « ul » ;

-          fait entrer dans son calcul les valeurs significatives des deux droites de régression, c'est-à-dire leurs coefficients directeurs.

2°) Interprétation de la corrélation et de la régression.

-          lorsque les points du nuage ne sont pas aligné, le cœfficient de corrélation « r » est , en « valeur absolue » , inférieur à « 1 »  (  - 1  <  r < + 1 ) .Les deux droites de régression sont alors « distinctes ». avec (  a . a’ < - 1 )

-          La fidélité de la représentation du nuage de points par les droites de régression est fonction de la valeur du coeffcient de corrélation « r » . Plus cette dernière ( en valeur absolue) approche de « 1 »  , plus cette « fidélité" est importante.

-          Si « r » est proche de « + 1 » , les deux phénomènes sont en relation étroite et leur sens de variation est identique : à un accroissement de « x » correspond un accroissement de « y » ( exemple : évolution salaire / prix)

-            Si « r » est proche de « - 1 » , les deux phénomènes sont en relation étroite, mais leur sens de variation est inverse . Dit autrement : à un accroissement de « x » correspond une diminution de « y » . ( exemple : évolution « température/ chauffage »)

-          si « r » est compris entre «  - 0,5 »  et  «  + 0,5 », il n’y a pas de véritable relation linéaire entre « x » et « y » . Cela peut provenir d’ une indépendance ou d’une relation non linéaire entre les deux phénomènes « x » et « y » ( exponentielle , hyperbolique, etc . ) Le nuage de points est dans ce cas très indicatif.

-          En fait , et règle générale , la corrélation :

                       est bonne     si     «   > 0, 8 »

                             est moyenne  si   «  0,5  <   > 0, 8 »

                              est mauvaise si  «    > 0, 5 »

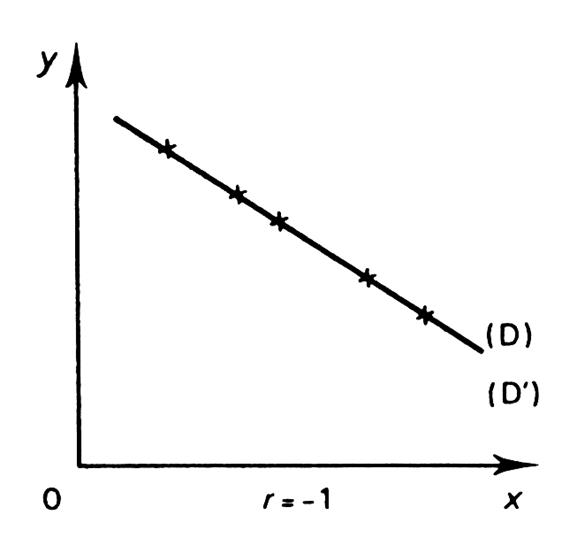
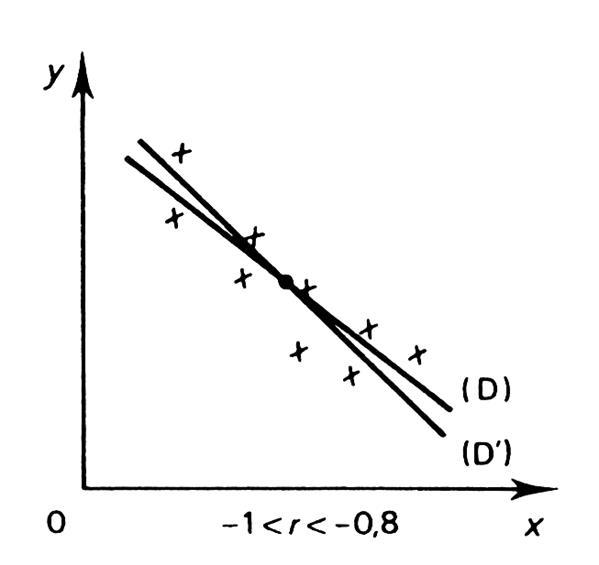
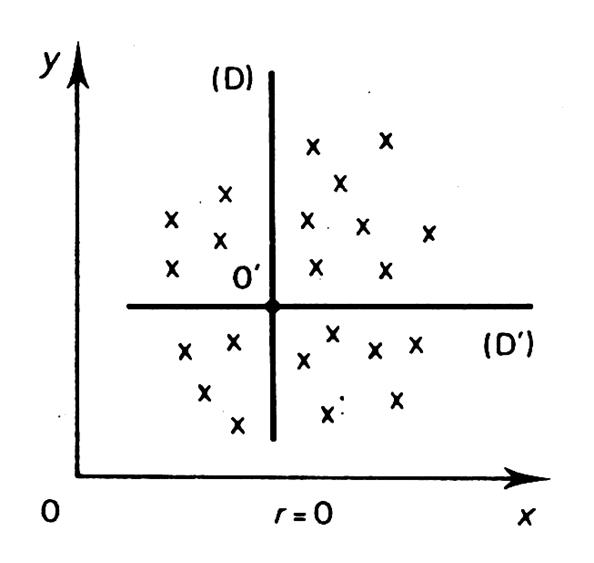
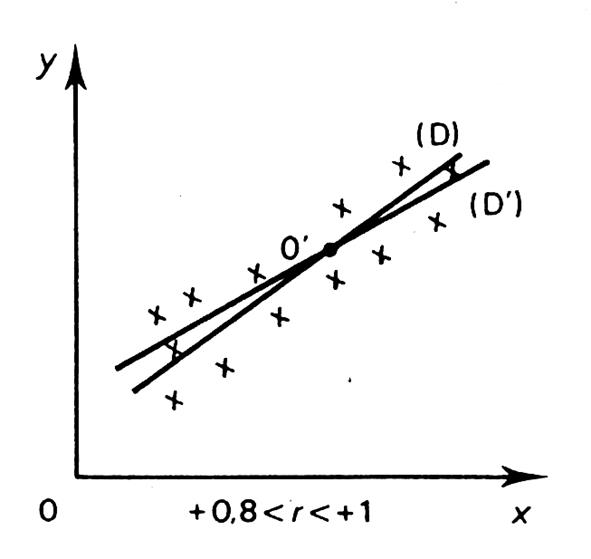
Ci-dessous , vous pouvez trouver quelques représentations graphiques typiques de corrélation.

-          la corrélation :

                       est bonne     si     «   > 0, 8 »

                             est moyenne  si   «  0,5  <   > 0, 8 »

                              est mauvaise si  «    > 0, 5 »

3°) Utilisation de la corrélation.

a)     Précaution liminaires.

Il n’est pas possible, à notre niveau, à partir de l’étude du coeffcient de corrélation, d’affirmer immédiatement l’existence d’une  « loi entre »deux phénomènes « x » et « y » , c'est-à-dire un lien de causalité entre « x » et « y » ou réciproquement. Nous devons , en effet, prendre garde aux « fausses corrélations ». Ainsi , il se pourrait que le coeffcient de corrélation entre le nombre de buts marqué au championnat de  France de  football  et le nombre d’accidents sur autoroute au cours des six derniers mois  soit proche de « + 1 » .Il est évident qu’il y aurait quelques dangers à établir une prévision sur l’un des phénomènes à partir de la connaissance de l’autre, car cette corrélation « fortuite » pourrait cesser brutalement.

D’ailleurs , pour des prévisions très précises, la corrélation est parfois insuffisante .Il faut  alors faire appel à des modèles économiques plus complexes. Dans ce sens , la corrélation n’est qu’un stade préparatoire permettant de sélectionner les variables « x » et « y » les plus satisfaisantes.

b)     Mise en œuvre pratique.

Pour des raisons pédagogiques nous  vous avons présenté l’étude de l’ajustement et de la régression avant celle de la corrélation.

Dans la pratique , le processus inverse, comme nous le présentons dans l’exemple suivant. :

Un gérant d’entreprise cherche à évaluer les frais de personnel d’un atelier de production pour l’année à venir. In va donc :

- procéder à une étude graphique, afin de rechercher les facteurs qui donnent, pour l’évolution des frais de personnel ,des nuages de points « resserrés », laissant entrevoir une étroite dépendance. Cela peut être par exemple :

Le nombre d’employés ( x ₁ )

Les heures de présence ( x ₂ )

Le taux du smig  ( x ₃ )

Le chiffre d’affaires ( x ₄ )

-          Rechercher  quel est le meilleur facteur explicatif ( variable  « x _n ») des variations des frais de personnel ( variable expliquée « y » ). Pour ce faire, il calculera les quatre coefficients de variation : « r  _{x1/ y ‘} » ; « r  _{x2/ y ‘} » ; « r  _{x3/ y ‘} » ; « r  _{x4 / y ‘} »

-          Choisir le coefficient le plus proche de « +1 » ( par exemple « x₄ ») et vérifier que la corrélation peut s’expliquer, qu’il ne s’agit pas d’une fausse corrélation.

-          Etablir ( s’il s’agit d’une relation linéaire), par la méthode des moindres carrés , la relation mathématique existante entre « x₄ » et  «  y » et obtenir une droite d’équation :

«  y = ax + b »

avec « y » = frais du personnel.

        « x » = chiffre d’affaires .

-          Demander au service marketing que est le chiffre d’affaires « fixé » par la direction pour l’année à venir ( x _v. ; »et déterminer ainsi les frais de personnel prévisonnels en effectuant le calcul :  

y  =  a x _v + b

Info ++

IV ) Utilisation des logarithmes pour le calcul du coefficient de corrélation.

Il est peut être intéressant  de calculer le coefficient de corrélation en utilisant les logarithmes

                        En effet

D’où  log r = log  -

De même les droites de régression peuvent, elles aussi, être calculées à partir de la même axiomatique :

Exemple : y = ax + b

 «  y  =   x + b

calcul de « a » :   a  =

d’où log de « a » = log   - 

FIN DU COURS .