LOGICIEL warmaths Pour Aide et Formation Individualisée

MECANIQUE

ICI pour aller directement aux informations « cours »

INFORMATIONS PEDAGOGIQUES :

DOSSIER N°

Matière : CINEMATIQUE

« TRAVAUX »

LES MOUVEMENTS

Classe : NIVEAU :

OBJECTIFS : - Savoir

I ) Pré requis: (pour remédiation ou mise à niveau)

i9

Mécanique ( Généralités)

:i

i9

cours spécifique sur @ la durée , @ travaux auto formatifs)

:i

II ) ENVIRONNEMENT du dossier :

Index

Dossier précédent : Mouvement - repos - repère.

Dossier suivant : Le mouvement rectiligne uniforme.

Info :

III ) INFORMATIONS «  formation leçon » :

Test

COURS

Travaux auto - formation.

Corrigé des travaux auto - formation.

Contrôle

évaluation

INTERDISCIPLINARITE

Corrigé Contrôle

Corrigé évaluation

Chapitres :

i9

:i

i9

:i

i9

:i

IV ) DEVOIRS ( écrits):

Devoir diagnostique L tests.

Ÿ

Devoir Auto - formatif (intégré au cours)

Ÿ

Devoir Formatif « Contrôle : savoir » ; (remédiation)

Ÿ

Devoir Formatif «  Evaluation  savoir faire » (remédiation)

Ÿ

Devoir sommatif.

Ÿ

Devoir certificatif : (remédiation)

Ÿ

* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .

Leçon	Titre
N°	LES MOUVEMENTS

COURS

I ) Généralités sur les mouvements.

1- Comment reconnaît -on qu’un corps est en mouvement ?

Voici une automobile sur la route , un avion dans le ciel . Vous dites qu’ils sont en mouvement par rapport au sol par ce que vous les voyez se rapprocher de certains objets et s’éloigner de certains autres fixés au sol. Au contraire , le clocher , les maisons du village , le pont sont des corps immobiles , ou fixes , ou en repos par rapport au sol. Ils nous servent de points de repère pour apprécier le mouvement de l’avion ou celui de l’automobile.

Pour étudier un mouvement , il est indispensable de se fixer des « repères » : leur ensemble constitue un système de référence invariable. Dans tout ce que nous allons aborder , nous prendrons le sol comme système de référence .Les astronomes , qui étudient les mouvements des astres , prennent les étoiles .

Dans un local , pour nous repérer , nous déplacer nous prenons comme référence le sol et deux autres murs perpendiculaires entre eux et perpendiculaires au sol.

Nous dirons donc que : Un corps est en mouvement par rapport à des repères fixes si ses distances à ces repères varient avec le temps.

2- La ligne qui suit un point mobile dans son mouvement est appelée : la trajectoire de ce point.

Exemples :

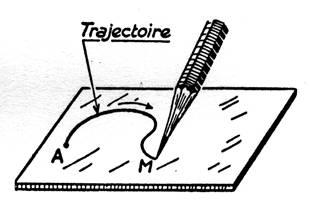
1- La point « M » du crayon se déplace sur le papier en laissant une ligne « AM » qui est la trajectoire du point « M ».

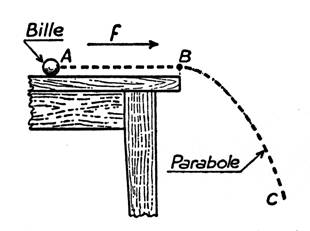
2 - La bille roule sur la table horizontale, puis tombe. Il ne reste aucune trace de sa trajectoire. Il en est presque toujours ainsi. La bille décrit d’abord une droite « AB » , sa trajectoire est « rectiligne » ; puis elle est « parabolique » lorsque la bille tombe.

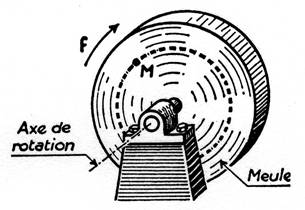
Un point « M » de la meule , tourne autour de son axe de rotation . Il décrit une circonférence. Sa trajectoire est circulaire.

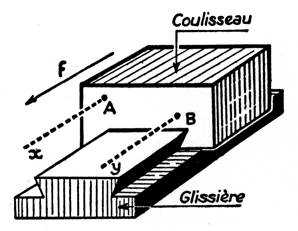
Tous les points tels que « A » et « B » du coulisseau décrivent des trajectoires rectilignes et parallèles. Le coulisseau est en mouvement de translation rectiligne.

III ) Pour étudier le mouvement d’un point sur sa trajectoire , il faut choisir une origine des distances et une origine des temps .

Premier exemple : Nous assistons à la course d’un 400 m haies .

Les coureurs sont sur la ligne de départ dans leur « storting bloc » , en un endroit précis tracé à la chaux sur le sol. C’est l’origine des distances.

Chacun d’eux devra courir dans un couloir bien tracé , lui aussi , à la chaux sur la piste. Ce couloir nous renseigne sur le trajet suivi par le coureur . ( la trajectoire).

Pour suivre de façon précise la course de chaque compétiteur , on utilise un chronomètre.

On déclenche à l’instant précis où le starter donne le signal du départ. C’est l’instant zéro « zéro » ou « origine des temps ».

Nous suivons la course de deux coureurs : Julien et Benoît :

- A la deuxième haie (point de repère sur la trajectoire) Julien a 1/10 de seconde d’avance sur Benoît

- A la cinquième haie ( autre point de repère ) Julien et Benoît sautent ensemble.

- A la huitième haie , Julien a de nouveau 1/10 de seconde d’avance sur Benoît.

Celui ci , sur un sursaut d’énergie , se lance et , à l’ »arrivée » , il a 2/10 de seconde d’avance sur Julien . Il a mis 51 ‘’ 5/10 et Julien 51’’ 7 / 10 .

Pour étudier le mouvement d’un point mobile sur sa trajectoire, nous ferons de même :

a) Nous définirons de façon précise la trajectoire ( droite , circonférence , hélice, etc.)

b) Nous choisirons un point de repère sur la trajectoire, que nous appellerons l’ « origine des distances » ;

c) Nous appellerons « distance de l’origine » la distance du mobile à ce repère, « distance mesurée sur la trajectoire » ;

d) Nous compterons les temps à partir de l’instant « zéro » ou « origine des temps », que nous choisirons arbitrairement , c’est à dire comme nous voudrons ( de la façon qui rendra les calculs les plus simples et commodes) ;

e) Si nous connaissons le mouvement du mobile, nous pourrons répondre à la question : Où est le mobile à tel instant ?

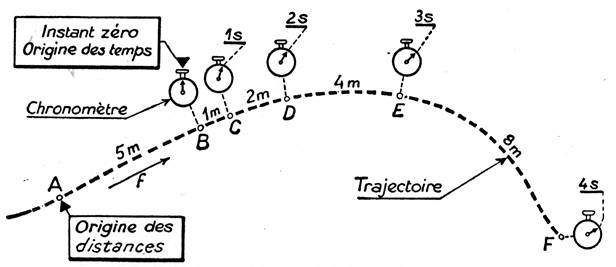
et à partir d’une situation , (voir le dessin ci dessous) nous pourrons dresser un tableau.

Temps comptés à partir de l’origine des temps ………..	0	1 s	2 s	3 s	4 s
Distance du mobile comptés à partir de l’origine des distances.	5 m	6 m	8m	12 m	20

L’origine des distances est le point fixe de la trajectoire à partir duquel on mesure les temps.

Dans l’exemple , nous remarquons que nous n’avons pas pris l’origine des temps à l’origine des distances:

« A » est l’instant « t » = 0 et « e ₀ » = 5 m ;

‘’ « t » = 1 et « e ₁ » = 6 m ;

‘’ « t » = 2 et « e ₂ » = 8 m

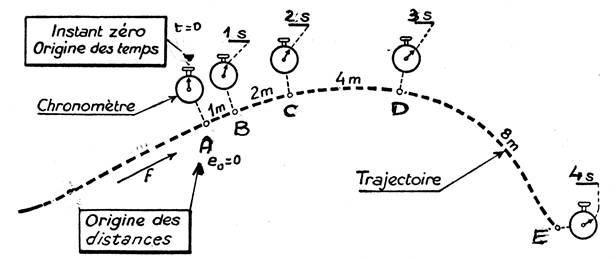
Attention : On a souvent intérêt à prendre comme origine des temps l’instant précis où le mobile est l’origine des distance ; alors à l’instant « t » = 0 ; « e ₀ » = 0 m ;

et à partir de cette nouvelle situation , (voir le dessin ci dessus) nous pourrons dresser un tableau.

Temps comptés à partir de l’origine des temps ………..	0	1 s	2 s	3 s	4 s
Distance du mobile comptés à partir de l’origine des distances.	0 m	1 m	3m	7 m	15 m

Dans ce nouvelle exemple , nous remarquons que nous avons pris l’origine des temps à l’origine des distances:

« A » est l’instant « t » = 0 et « e ₀ » = 0 m ;

‘’ « t » = 1 et « e ₁ » = 1 m ;

‘’ « t » = 2 et « e ₂ » = 3 m

ect. ………………

Leçon	Titre
N°	TRAVAUX d ’ AUTO - FORMATION sur LES MOUVEMENTS

TRAVAUX N° d ’ AUTO - FORMATION : LES MOUVEMENTS CONTROLE

TRAVAUX N° d ‘ AUTO - FORMATION LES MOUVEMENTS EVALUATION