Module : Géométrie				DOSSIER : 190
LOGICIEL warmaths  ; Pour Aide et Formation Individualisée ; REMEDIATION mise à /NIVEAU : niveau VI
Info conseils et consignes.	TRAVAUX NORMATIFS PRIMAIRE / COLLEGE /LYCEE Matière : MATHEMATIQUES. Niveau VI et niveau V							.Corrigé
Corrigé : PRISMES DROITS. Calcul de la hauteur ; calcul de la surface de base.
INFO COURS :
Info 1 @ « cours sur les calculs sur les prismes droits… » ;
TRAVAUX CONTROLE
Les questions relatives à « ce qu’il faut retenir » , au « savoir » se reporter aux cours .
TRAVAUX : EVALUATION
Calcul de la hauteur, calcul de la surface de base. La formule : Volume = surface de base ´ hauteur permet de calculer le volume d’un prisme droit, d’un cylindre. Inversement, si on divise le volume par une des deux grandeurs dont on a fait le produit, on trouve l’autre grandeur. Volume : surface de base = hauteur ; Volume : hauteur = surface de base Mais il faut toujours opérer avec des nombres exprimant les mesures en unités correspondantes.
Que puis-je calculer ? Posez la question, répondez-y 1. 4,5 m^3de sable sont répandus dans une cour en couche d’égale épaisseur 5 cm. Quelle est la surface de sable couverte ? On convertit l’épaisseur 5 cm en 0,05 m Puis on divise 4,5 par 0,05 = 90 m² ( lire : 90 mètres carrés) 2. La citerne d’une ferme a une base carrée de 2,4 m de côté et contient 14,4 m^3d’eau. Quelle est la surface au sol de la citerne ? On calcule 2,4 m par 2,4 m = 5,76 m² Quelle est la hauteur de la citerne ? On divise 14,4 m^3 par 5,76 m² = 2,5 m 3. 35 élèves et le maître ont chacun 5 m^3d’air dans une salle de 9m sur 5 m. 1. Quel est le nombre de personnes dans la classe : 35 + 1 = 36 ^2.Quel est le volume d’air nécessaire : 5 fois 36 = 180 m^3 3. Quelle est la surface de la classe ? : 9 fois 5 = 45 m² 4. Quelle est la hauteur de la classe ? : 180 m^3 divisé par 45 m² = 4 m 4. Copiez et complétez ce tableau, qui concerne des parallélépipèdes rectangles.
Volume		576 cm^3	900 cm^3		44 m^3	73,92 m^3	35,6 m² x 3, 05 m= 108,58 m^3		408 d m^3
Surface de base		96 cm²	120 cm²		16 m²	3,92 : 2,8= 26,4 m²	35,6 m²		48 dm²
Hauteur		576 :96=…6 cm.	…7,5 cm..		2,75 m…	2,8 m	3 , 05 m		8,5 dm
5. Dans une cour d’école, on déverse 14 camions de sable de 2,4 m^3chacun. Le sable étendu forme une couche- uniforme de 4 cm d’épaisseur. a) Quelle est la surface de la cour? 1°) volume de sable répandu : 14 fois 2,4 m^3= 33,6 m^3; 2°) convertir 4cm = 0,04 m ;3°)surface couverte par le sable : 33,6 m^3: 0,04 m^1= 840 m² b) Elle a 24 m de large; quelle est sa longueur ? longueur de la cour : 840 m² / 24 m= 35 m 6. A 27 € m ^3, le sable d’un sautoir a coûté 94,50 € . Le sautoir étant un parallélépipède rectangle de 7 m de long et 2 m de large, quelle est l’épaisseur du sable? Volume de sable utilisé : 94,50 € / 27 €/m^3 = 3,5 m^3 ; Surface du sautoir : 7 m fois 2 m = 14 m² ; calcul de l’épaisseur de sable : 3,5 m / 14 m = 0,25 m , soit 25 cm 7. On construit un réservoir cylindrique pour une commune de 1 800 habitants. On estime à 35 L d’eau par jour la consommation de chaque habitant. a) Quel doit être le volume du réservoir pour que la réserve d’eau soit assurée pour 3 jours? b) Le réservoir ayant 6 m de diamètre, quelle sera alors, à 1 cm près, la hauteur de l’eau? 1. Consommation pour un jour : 1800 fois 35 L=63 000 L ; 2. Consommation pour 3 jours : 63 000 fois 3 = 189 000 L 3. Volume d’eau : 189 000 L = 189 000 dm^3 = 189 m^3 4. Surface de base du réservoir : 3,14 fois 3 fois 3 = 28,26 m². 5. Hauteur de l’eau dans le réservoir : 189 m^3/ 28,26 m² = 6,6878 soit au cm prés : 6,69 m 8. L’eau potable d’une ferme est fournie par l’eau de pluie tombant sur un toit et recueillie dans une citerne. Le toit a deux pans de 16,5 m sur 5,4 m. Au cours d’un orage, il est tombé 15 mm d’eau. a) Quel est le volume de l’eau recueillie ? 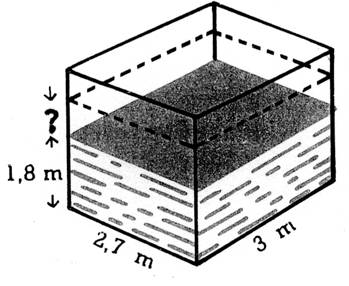· surface du toit : 2 fois 16,5 sur 5,4 = 178,2 m² ^·volume d’eau recueilli : 178,2 m² fois 0,015 m= 2,673 m^3 b) La citerne est un parallélépipède rectangle de 2,7 m de large et 3 m de long, qui contenait une hauteur d’eau de 1,8 m avant l’orage. Quelle hauteur en contient-elle après l’orage ? 1. Volume contenu après orage : ( 2,7 fois 3 fois 1,8 ) + 2,673 m^3 = 14,78 + 2,673 = 17,253 m^3 2. Surface de base de la cuve : 2,7 m fois 3 m = 8,1 m² 3. Hauteur d’eau contenue dans la cuve après orage : 17,253 / 8,1 = 2,13 m 9. Un tas de bois de 2 m de long et 0,8 m de haut est fait de bûches de 1,2 m de long. On scie ces bûches, chacune en 4 morceaux égaux et l’on range ces morceaux en une seule pile contre un mur de 4 m de long. A quelle hauteur s’élève la pile ? 1,2 / 4 = 0,30 m la longueur d’une buche. Soit 4 tas de 2 m long par 0,80 m de haut. Par déduction le tas de bois fait 1,60 m de haut. Calcul rapide : 10. Quelle est la hauteur d’une salle rectangulaire quand son volume et sa surface de base sont : 80 m^3et 20 m ^2= 8/2 = 4 m?; 45 m^3et 15 m ^2= 3 m?; 75 m^3et 30 m ^2= 7,5 / 3 = 2,5 m?; 64 m^3et 20 m = 6,4 /2 = 3,2 m ?;