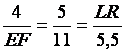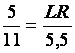Mathématiques :
(donné à Wassigny 02)
DEVOIR
SURVEILLE : Le 4 octobre 2010
|
|
Problèmes : |
|
|
|
|
|
|
|
Exercice 1 : ( 3 pts.)
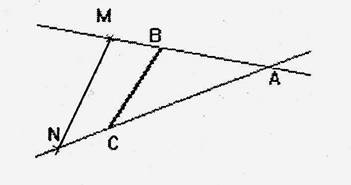
On donne ( en cm) : AM = 7 ; AB = 3 ; AN = 9 ; AC = 5 Les
droites BC et NM sont-elles parallèles ? justifier |
|
|
|
D’après la
propriété de Thalès : BC et MN sont parallèles si on vérifie que les
rapports suivants sont égaux : Si Donc : on se pose la
question : On fait le produit en croix : 3 x 9 = 27 ; 7 x 5 = 35 ; Il s’avère
que 3/ 7 et
5/9 ont des résultats différents . On peut en conclure que les droites BC et NM ne sont pas parallèles. |
|
|
|
Exercice
2 : ( 3 pts.) |
|
|
|
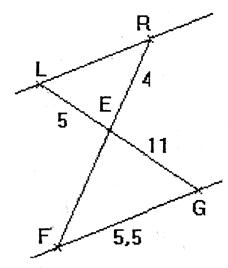
Les droites ( L R) et ( FG) sont parallèles. Unité : cm. Calculer les
longueurs : LR et EF . ( arrondir au dixième si
besoin est) |
|
|
|
Les droites LR et
FG sont parallèles si ·
On remplace dans les lettres par les valeurs données : ·
On extrait une première égalité de deux rapports (dont on connaît 3
valeur sur 4) : Nous pouvons
calculer la valeur de EF : 4 x 11 =
5 EF 44
= 5 EF ou 5 EF = 44 ; EF = 44 / 5 ; EF = 8,8 ·
On extrait une deuxième égalité de deux rapports dont on connaît 3
valeurs sur 4 : 5 x 5,5
= 11 LR 11 LR
= 27,5 LR = 25,5 / 11 LR =
2,5 |
|
|
|
Exercice
3 : (2 pts.) |
|
|
|
Construire au compas le
point M de [AB] , tel que :
|
|
|
|
Réponse : 1°) Tracer une
droite (D) passant par A (angle A
environ 60°)par rapport au segment AB. 2°) A l’aide d’un
compas d’ouverture environ 2 cm , Mettre la pointe
en A ; tracer un arc de cercle coupant (D) , noté « F » ,
déplacer la pointe et la placer en
« F » ; tracer 6 arcs
coupants la droite D , pour obtenir 6 segment de droites de même longueur. ( nommer
les points : F ; G ; H ; I ; J ; K.) 3°) Au bout du
dernier segment nommé le point K 4°) Tracer une
droite passant par e point K et le point B . ( cette droite est la droite « direction » ) 5°)
Tracer une droite parallèle à KB passant par K . Cette droite coupe le segment AB en
« M » ;
6°) AM se trouve
être les 5/6 de AB |
|
|
|
Exercice
4 ( 3 pts.) |
|
|
|
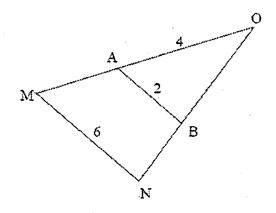
Les droites (MN) et ( AB) sont
parallèles. L’unité est le cm. Calculer le coefficient de
réduction entre les deux triangles.
|
|
|
|
Calcul de MO : On établit l’égalité des rapports : On remplace dans l’égalité
précédente : Calcul de OM = ( 6 x 4 ) / 2 = 12 Le coefficient de réduction est de
1 / 3 |
|
|
|
Exercice
5 ( 5 pts.) |
|
|
|
L’unité de longueur est le
centimètre. 1. a) Tracer un cercle C1
de centre « O »et de diamètre [ AB] tel que AB = 10 b) Placer le point
« C » du segment [ AB] tel que AC = 6 c) Tracer un cercle C2 de diamètre [ AC] et le cercle C3 de diamètre [ BC]. d) placer un point
« D » du cercle C1 tel que BD = 5 e) La droite ( AD) recoupe C2 en « E ». 2. Démontrer que
« ADB »est un triangle rectangle. 3. Démontrer que les
droites ( BD ) et ( CE ) sont parallèles. 4. a) Calculer EC. b) Calculer AE. En déduire ED. |
|
|
|
Exercice
6 : ( 5 pts.) |
|
|
|
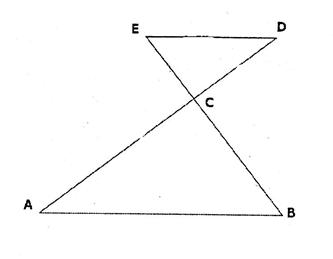
On donne (en cm) CE = 5 ; CD = 12 ; CA = 18 ; CB = 7,5 ; AB
= 19,5 a) Montrer que les droites (ED) et (AB)
sont parallèles. (ED) et (AB) sont parallèles si on vérifie l’égalité : On
remplace les lettres par les valeurs et l’on calcul le produit en croix. Produit en croix : 7,5 x 12
= 90 ; 5
x 18 = 90 Conclusion :
les deux rapports sont égaux , on peut en conclure
que (ED) et (AB) sont parallèles b) Montrer que ED = 13 On sait que :
ED = 234 / 18 ED = 13 c) Montrer que le triangle CED est un
triangle rectangle. : Le triangle EDC est rectangle
si (ED)²
= ( EC)² + (CD)² Donc :
(13)² = ? = ( 5)² + (12)² a) ( 13)²
= 169 b) ( 5)² + (12)² = 25 + 144 ( 5)²
+ (12)² = 169 On peut conclure
que ED est l’hypoténuse du triangle EDC . Le triangle EDC est rectangle.
|
|
|
|
|
|
|
|
|
|
|
|
|
|