DOSSIER :  LE  « MODE »    et   « classe modale » d’une série statistique.

1°) définitions : mode et classe modale d’une série statistique.

2°) Détermination de la valeur du mode d’une série statistique.

A ) caractère ou variable discontinue : à partir d’un tableau ; à partir d’un graphique ; d’une « série bimodale ».

B) Dans le cas d’une variable continue.( Propriétés )

COURS

1° ) Définitions :

1°)  Le mode est une caractéristique de position ( dit aussi de « tendance centrale »)

L’abrégé de « mode » est « m »  ou « Mo »  d’où la notation :  « m »  ou «  Mo »

Par définition : Un mode d’une série statistique est une valeur du caractère correspondant au plus grand effectif ( ou à la plus grande fréquence.)

Vocabulaire   à connaître  :

On dit « mode » d’une série à variable discrète .

Et « classe   modale»  d’une série à variable continue …

               Généralement , lorsque  les valeurs sont groupées en classe. La classe correspondant au plus grand effectif est appelée « classe modale ».

On reteindra :    le mode est la valeur de la variable qui correspond à l’effectif maximal ou à la fréquence maximale.

Ainsi pour identifier le mode il faut rechercher l’effectif ou la fréquence maximal.

2°) Détermination de la valeur du mode d’une série statistique :

Commentaire :

Le calcul concerne deux cas : cas d’une variable (caractère) discontinue et cas d’une variable (caractère)  continue.

 A ) caractère ou variable discontinue : le mode se détermine très simplement , ainsi que l’on peut le voir dans l’exemple suivant :

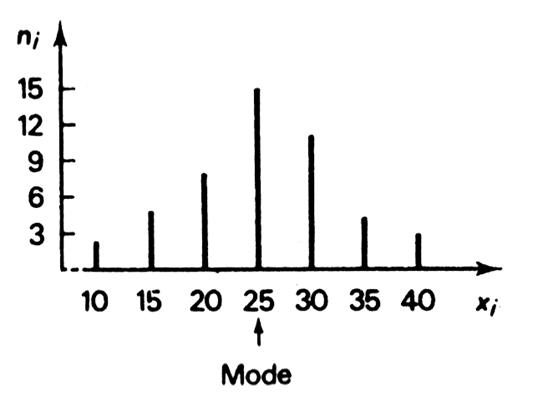
A partir d’un tableau :

Procédure pour « identifier » le mode:

1°) Dans le tableau , on recherche l’ effectif le plus important .

2°)Faire  correspondre la valeur du « x _i »  qui indiquera la valeur du mode :

ici « 25 ».

 _i

Effectifs :  _i

10

2

15

3

20

8

       mode

25

◄        17

30

13

35

5

40

3

A partir d’un graphique :

Sur le graphique de distribution, le mode correspond au « bâton » le plus élevé. Sa valeur est donnée par l’axe des abscisses.

Lorsqu’il n’y a qu’un mode , la série est dit « uninominale ».

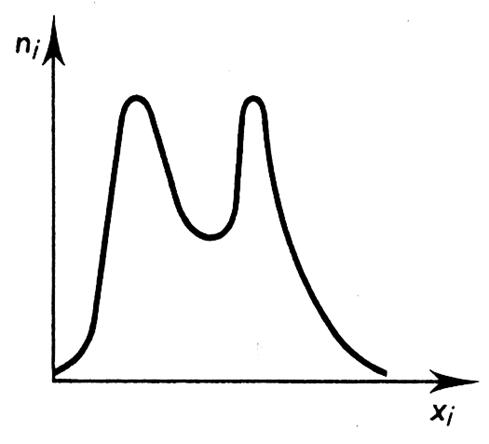
Quand la série possède deux valeurs admettant des effectifs maximaux égaux, elle est appelée « série bimodale ».

B) Dans le cas d’une variable continue.

Comme nous l’avons déjà écrit précédemment …..

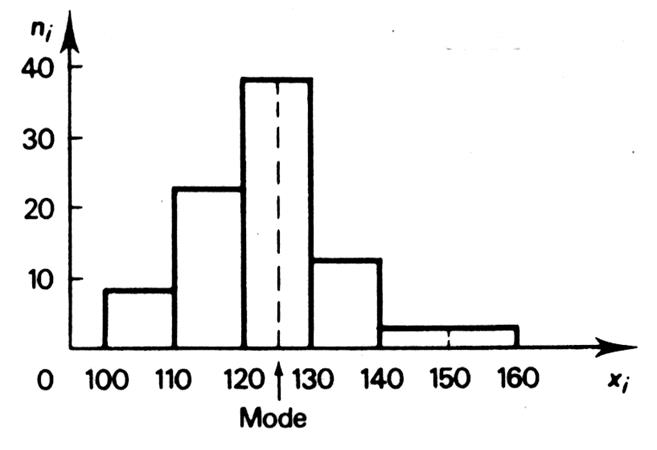
Le mode  s’applique à la classe qui correspond à l’ effectif maximal. Celle - ci s’appelle « classe modale » .

Classes :   xi

Effectifs   n_i

100 à 110

8

110 à 120

22

Classe   modale     120 à 130

38

130 à 140

12

140 à 150

6

total

86

Une valeur précise peut être affectée à la caractéristique en prenant , par convention , le mode  , comme étant ,  égal au centre de la classe.

Attention : 

Rappelons que la valeur du mode, dans ces conditions, dépend de l’amplitude des classes, et qu’il faut vérifier « l’égalité » des intervalles de classes.

Remarque :

A première vue, il semblait que la classe modale soit comprise entre 110 et 120. En fait et après correction des amplitudes, c’est la classe de 120 à 130 qui représente la classe modale.

Classes :   xi

Effectifs   n_i

100 à 110

8

110 à 120

22

120 à 125

     18

←

38

125 à 130

     20

130 à 140

12

140 à 160

6

86

Nous le vérifions d’ailleurs sur l’histogramme. La valeur « 125 », centre de classe , peut être appelée « mode ».

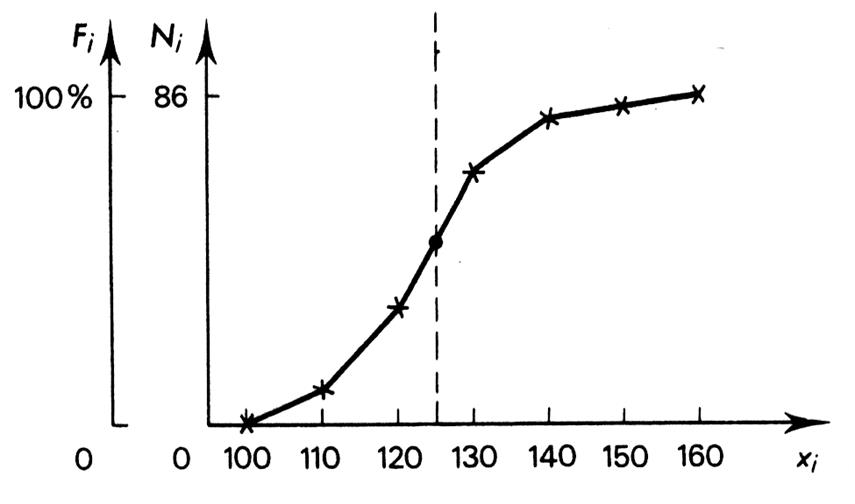
Propriétés :Sur la fonction de répartition , la valeur du mode correspond à l’abscisse  du point d’inflexion de la courbe. En effet , au delà de ce point le taux de croissance de la courbe diminue.

Suite :► la médiane

Dans le tableau ci contre : Trouver la classe modale :

Réponse dans le cours.

Classes :   xi

Effectifs   n_i

100 à 110

8

110 à 120

22

120 à 130

38

130 à 140

12

140 à 150

6

total

86

Dans le tableau ci contre :

Déterminer le mode

Classes :   xi

Fréquences  f_i

0 - 10

1

10 - 20

3

20 -30

4

30 - 40

2

total