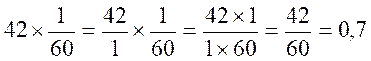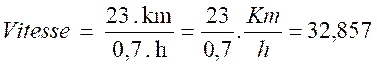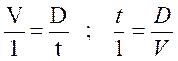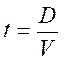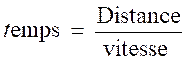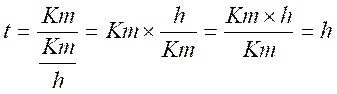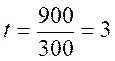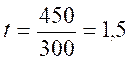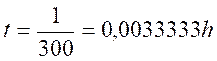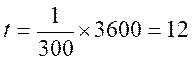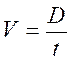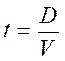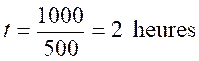|
DOC : Formation Individualisée |
|
DOSSIER N° 9 Matière : mathématique / Calcul numérique. |
Information
« TRAVAUX » |
|
PREPARATION CONCOURS pour gendarmerie et police |
OBJECTIFS :« CALCUL
Numérique » Addition , soustractions, multiplication, division, puissance ,
racine carrée |
I ) Pré requis:
|
i9 |
:i |
|
|
i9 |
:i |
|
|
i9 |
:i |
|
|
i9 |
:i |
|
|
|
|
|
II ) ENVIRONNEMENT du dossier :
|
Dossier précédent : |
Dossier suivant : |
Info : Liste des leçons à étudier pour le
concours de la gendarmerie et de la police. |
|
|
|
|
|
|
|
|
|
|
|
III )
LECON n° 9 : LES VITESSES
( moyennes)
Chapitres
:
|
i9 |
:i |
|
|
i9 |
:i |
|
|
i9 |
:i |
|
|
i9 |
:i |
|
|
i9 |
:i |
IV) INFORMATIONS
« formation leçon » :
|
Travaux auto -
formation. |
|
Corrigé des
travaux auto - formation. |
||||
|
Corrigé |
||||||
|
|
|
|
||||
V ) DEVOIRS ( écrits):
|
Devoir diagnostique L tests. |
|
|
Devoir Auto
- formatif
(intégré au cours) |
|
|
Devoir Formatif « Contrôle :
savoir » ; (remédiation) |
|
|
|
|
|
Devoir sommatif. |
|
|
Devoir certificatif : (remédiation) |
|
* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .
|
Titre |
|
|
N°9 |
Lorsque l’on parle de « vitesse » on doit faire la différence entre une vitesse
moyenne ; une vitesse moyenne instantanée ; de vitesse « accélérée » ou de
vitesse « décélérée »….
Ces vitesses se calculent : c’est toujours le rapport
d’une distance parcourue par une unité de temps….. (il
faut voir cas par cas…)
Commentaire : En voiture ,
les vitesses excessives sont sources d’accident plus ou moins grave.
Pour stopper un véhicule il faut de la rapidité
d’esprit (avoir conscience qu’un danger va arriver) ,
appuyer sur la pédale de frein , attendre
que le véhicule s’arrête .
Ainsi :
Ainsi à la distance de freinage faut -il ajouter la
distance parcourue entre le moment ou l’on prend conscience que l’accident peut arriver et le
moment ou l’on va appuyer sur la pédale .
|
i9 |
:i |
Une
vitesse est une distance parcourue pendant
une unité de temps. Mathématiquement, c’est le quotient d’une distance par un temps.
Ce
qui nous donne l’égalité. 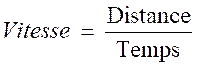
ou
par l’équation 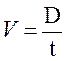
La
vitesse s’exprime généralement en Km
/h (noté aussi : km.h-1 ) ou en
m /s (noté aussi :
m.s-1)
*
Km / h :
lire « kilomètre par heure »
; m/ s : lire « mètre
par seconde »
**
Ainsi : « pour une vitesse
de
***
Et : « pour une vitesse
de
|
i9 |
Conversions : passage des Km / h à des m / s |
:i |
Rappels : 1 k m = 1 000 mètres ; et 1 heure = 3600 secondes
Exemple :
convertir
Cette
conversion s’opère en deux étapes :
a)
convertir les kilomètres en mètres (
b)
J’effectue le calcul : 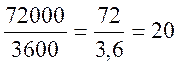
Conclusion :
à la vitesse de
En
résumé : pour obtenir une vitesse
en mètre par seconde , il faut diviser la vitesse en Km/h par 3,6
Soit
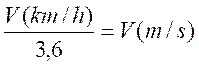 ;
;
Remarque : Dans le code de la route on préconise de diviser la vitesse exprimée
en Km/h par « 3 » ; ce nombre correspond
« approximativement » à la distance parcourue ( en mètres) par un
véhicule ,en 1 seconde .
Pour
avoir une idée de la distance qui sera
parcourue par un véhicule entre le moment ou le
conducteur * constate un risque et le moment ou il
freine .Il faut donc diviser la vitesse
affichée sur le compteur par 3 .
* on considère qu’il faut au minimum 1
seconde de réflexion avant de freiner ; attention il faut
,bien entendu, que cette distance
s’ajoute à la distance de freinage du véhicule !!!!!)
Activités :
|
Vitesse en Km / h |
A
Convertir ces vitesses ;
en m/s .(calcul théorique) |
A Convertir ces vitesses ,les exprimer en m/s : Résultat approximatif :( code de la route) |
|
320
(voiture de course) |
|
|
|
180 |
|
|
|
130
(sur autoroute) |
|
|
|
110 |
|
|
|
90 (sur route) |
|
|
|
80 (apprenti) |
|
|
|
60
|
|
|
|
50
(en ville) |
|
|
|
30
(vélo) |
|
|
|
20
«marathon man) |
|
|
|
10 |
|
|
|
Marche rapide
5 |
|
|
|
Marcheur :
3 |
|
|
|
i9 |
Conversions : passage des m / s à des Km / h |
:i |
Cette
transformation se fait en deux
temps : (exemple :
|
J’ai
une vitesse en m / s , je vais
calculer le nombre de mètre qui sera parcourue en 3600 s ( = 1heure) |
Soit 30 fois 3600 = |
|
Je
divise par 1000 le nombre 108 000 pour obtenir des « Km » |
Soit |
|
Conclusion : à
|
|
En
résumé : pour convertir une vitesse exprimée en m/ s en Km
/ h je multiplie le nombre de mètre par
seconde par 3600 et je divise le résultat par 1000.
Soit : 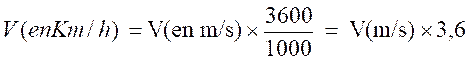
Ce
qui donne la formule ![]()
- Pour le code
de la route on multipliera par « 4 » !!!!!!!
|
i9 |
Autres
conversions : des k m / h en k m / s
ou vis versa !!! |
:i |
Exemple : les satellites dans
l’espace se déplace à la vitesse de
Exemples résolus :
N°1.
|
Convertir |
Pour
obtenir la vitesse en 1 seconde, Il suffit de diviser les 21600 km
par 3600 secondes. Soit 21600 : 3600 = 6 Conclusion : |
Si on avait demandé une vitesse exprimée en mètre par seconde
, on convertissait les
on
conclut que la vitesse de
Un
véhicule qui se déplace à la vitesse de
N°2
|
Convertir 0,6 k m /s en
m /s |
Il
suffit de multiplier les kilomètres par 1000. Soit 0,6 ´ 1000 = 600 Conclusion : 0,6 k m /s = 600 m /s |
N°3
|
Convertir des |
Il
suffit de multiplier les Km par 3600 Soit 15 ´ 3600 = 54 000 Conclusion : |
|
i9 |
:i |
Commentaires préalables :
Les
problèmes fondamentaux sont le calcul d’
un temps , d’une distance ou d’une vitesse.
Attention,
il faut prendre garde de ne pas mélanger
les unités dans la formule :
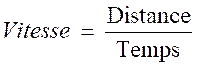
par
exemples :
Si
la vitesse est exprimée en Km/h , la
distance se lira en kilomètre et le temps en heures.
Si la distance est exprimée en mètres et le temps en heures, la vitesse sera
exprimée en m/h.
Attention : 1 h 30 min
= 1,5 h ou =
60 +30 = 90 min , et 45 min =
0,75 h
Et que : 42 min =
(42 / 60) h = 0,7 h
ou 42 min = 42 fois 60 s = 2520
s
Lorsque
le temps est donné en minutes, on
choisira de convertir ce temps en
« heure » ou en « secondes »
PROBLEME N°1 :
Enoncé :
Calculer la vitesse en m/s et Km / h
d’un vélo qui parcourt
Ce
problème peut être résolu de deux façons.
Solution
1 :
On transforme la distance en mètres et le temps en secondes pour obtenir une vitesse en m / s. Puis on transforme la vitesse obtenue
en Km/h.
Procédure :
|
On
convertit les minutes en secondes |
42
´ 60 = 2520 s |
|
On
convertit les kilomètres en mètres |
|
|
On
calcule la vitesse en m / s |
23 000 ¸
2520 = …….»
9,12 m / s |
|
On
calcule la vitesse en km / h : - Soit avec la formule :
-
Soit en calculant la distance en mètre
par heurs puis on convertit en Km / h |
1er calcul : Autre
calcul : 9,12
´ 3600 = et (32 800
/ 1000) Km/h = |
Solution
2 :
On conserve la distance en kilomètres et
l’on transforme le temps exprimé dans le système sexagésimal (h / min / s ) en temps exprimé
dans le système décimal. ( nombre « à virgule »)
|
On
convertit 42 minutes en nombre décimal
d’heure. Une
minute représente 1/ 60ème
d’heure. 42
minutes = 42 fois 1/ 60ème . |
soit |
|
A
partir de la formule :
on
calcule « V » |
D
= T
= 0,7 h Donc |
|
Conclusion : la vitesse est de |
|
|
On
remarque que l’on a choisi 3 chiffres après la virgule ; le résultat est
exprimé en Km/h ; au mètre par heure prés. |
|
PROBLEME
N°2.
Enoncé : Un train à grande vitesse parcours
une distance de
Résolution :
|
On
utilise la formule Soit On
en déduit (d’après le produit en croix)
ce
qui se traduit Pour retrouver
l’unité :
|
D
= V
= Calcul
du temps :
Conclusion :
le train mettra 3 heures pour
parcourir les |
PROBLEME
N°3.
Enoncé : Un train à grande vitesse parcours
une distance de
Résolution :
|
On
utilise la formule Soit On
en déduit (d’après le produit en croix)
ce
qui se traduit Pour retrouver
l’unité :
|
D = V = Calcul
du temps :
Conclusion 1: Le
train mettra 1,5 h pour parcourir les Puisque ( 0,5 h = 0,5 ´60
= 30 minutes) Ou
Conclusion 2: On
pourra dire : Le
train mettra 1 h et 30 minutes pour
parcourir les |
PROBLEME
N°4.
Enoncé : Un train à grande vitesse
traverse un tunnel de
Résolution :
|
On
utilise la formule Soit On
en déduit (d’après le produit en croix)
ce
qui se traduit Pour retrouver
l’unité :
|
D = V = Calcul
du temps :
Ce
résultat ne « disant » rien, on sait qu’il y a 3600 secondes en 1
heure. On multipliera ce calcul par « 3600 » Soit
Conclusion 1: Le
train mettra 0,003333 h pour parcourir 1
km. Puisque ( 0,003 3333 h = 0,003333 ´3600
= 12 secondes) Ou
Conclusion 2: On
pourra dire : Le
train mettra 12 secondes pour
parcourir 1 km. |
PROBLEME
N°5
Un
jeune automobiliste roule à
|
Commentaire
|
Résolution. |
|
La
formule à utiliser est :
Il
faut mettre « 1h 45min »
sous forme décimale. |
1h
45min = 60 min + 45 min = 105 min et
105 min / 60 min = 1,75 heure. Si
D
= 80 ´ 1,75 = |
|
Conclusion :
la distance parcourue en 1 h 45 min à |
|
PROBLEME
N°6
Les
villes A et B sont distantes de
|
Commentaire
|
Résolution. |
|
On
va chercher combien de Km sont parcourus en 1 heure. La
distance à parcourir est de On
sait que : |
a) Les deux trains se rapproche à la vitesse de 300 + b) de soit :
c)
Pour parcourir la distance qui les sépare , ils mettront 2 heures. d)
Conclusion : ils se croiseront donc à : 10
h 30 min + 2 h = 12 h 30 min. |
|
i9 |
:i |
Exemple : Une voiture de rallye fait
Il
a parcouru 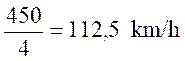
Si
on calcule la moyenne des vitesses, on obtient : 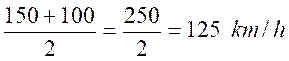
ATTENTION :
la moyenne des vitesses n’est pas égale à la vitesse moyenne. !!!
Si vous partez en vacances la vitesse moyenne en voiture est généralement compris entre
60 et
Sur un trajet long, on s’arrête !!!!
Pour
calculer la vitesse moyenne d’un véhicule à partir de deux vitesses, il faut
calculer la distance totale parcourue et
diviser par le temps total.
On
retiendra : 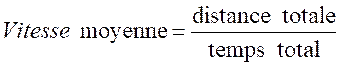
|
Leçon |
Titre |
|
N°9 |
TRAVAUX d ’ AUTO -
FORMATION sur
L ES VITESSES |
TRAVAUX N°9
d ’ AUTO - FORMATION :
CONTROLE
1°) Donner la définition de la vitesse.
2°) Donner la
formule permettant de calculer la vitesse.
3°) A quoi est égale la vitesse
moyenne ?
TRAVAUX
N°9 d ‘ AUTO - FORMATION EVALUATION
|
Vitesse en Km / h |
Convertir en m/s : |
Convertir en m/s : Par
approximation :( code de la route) |
|
(F1)
320 |
|
|
|
180 |
|
|
|
130 (sur autoroute) |
|
|
|
110 |
|
|
|
90
(sur route) |
|
|
|
80
(apprenti) |
|
|
|
60 |
|
|
|
50 (en ville) |
|
|
|
30 (vélo) |
|
|
|
20 «marathon man) |
|
|
|
10 |
|
|
|
Marche
rapide 5 |
|
|
|
Marcheur : 3 |
|
|
|
|
|
|
N°1.
|
Convertir 21 600
km / h en km/s
; Puis
en m/s |
|
N°2
|
Convertir 0,6 k m /s ;
en m /s |
|
N°3
|
Convertir
des |
|
PROBLEME
N°1 :
Enoncé : Calculer la vitesse en m/s
et Km / h d’un vélo qui
parcourt
PROBLEME N°2
Enoncé :
Un train à grande vitesse parcours une distance de
PROBLEME N°3.
Enoncé :
Un train à grande vitesse parcours une distance de
PROBLEME N°4.
Enoncé :
Un train à grande vitesse un tunnel de
PROBLEME N°5
Un jeune
automobiliste roule à
PROBLEME N°6
Les villes A et B sont distantes de
|
|
|
|
N°
|
Enoncés.
|
Corrigé
|
|
|
Convertissez
en m/s -
vitesse d’un vélo à
38,8 Km/h : -
Vitesse d’une voiture à |
|
|
|
Convertir
en Km/h : -vitesse
d’un marathonien à 5 m/s : -
vitesse d’un cyclomoteur à 12,5
m /s |
|
|
|
Calculer
la vitesse en Km/h : -
d’un avion qui parcours -
D’un train qui traverse un tunnel de |
|
|
|
Calculer
la distance parcourue par : -
un camion en 12 minutes à 75 Km/h : -
Un coureur cycliste
en 45 minutes à -
Un motard en 18 minutes à 120 Km /h. |
|
|
|
Calculer
le temps de chacun des parcours suivants : -
-
-
1,5 Km à pied en courant à |
|
|
|
Un
train part de Paris à 10 heures vers Bordeaux, éloignée de Un
second train part de Poitier à 11 h 25
minutes vers Bordeaux , éloignée de |
|
|
|
Les
villes de Lyon et de Paris sont
séparées de |
|
|
|
Une grand rue a une longueur de |
|
|
|
Un
automobiliste met 8 heures pour aller
de Paris à Monpellier. Sachant que la distance
entre ces deux villes est de |
|
Vitesse
moyenne :
|
|
Un représentant de commerce à domicile a
parcouru |
|
|
|
Un
randonneur effectue : |
|
|
|
Un
cycliste parcourt : Puis
Et puis
Quelle
est sa vitesse moyenne ?. |
|
CORRIGE
|
N°
|
Enoncés.
|
Corrigé
|
|
|
Convertissez
en m/s -
vitesse d’un vélo à
38,8 Km/h : -
Vitesse d’une voiture à 80 Km/h : |
|
|
|
Convertir
en Km/h : -vitesse
d’un marathonien à 5 m/s : 5 fois 3600 = 18 000 m/h = -
vitesse d’un cyclomoteur à 12,5
m /s |
|
|
|
Calculer
la vitesse en Km/h : -
d’un avion qui parcours (560 : 45 ) fois 60 = -
D’un train qui traverse un tunnel de ( 290 m : 7,2 s
) fois 3600 s = |
|
|
|
Calculer
la distance parcourue par : -
un camion en 12 minutes à 75 Km/h : -
Un coureur cycliste
en 45 minutes à -
Un motard en 18 minutes à 120 Km /h. |
|
|
|
Calculer
le temps de chacun des parcours suivants : -
-
-
1,5 Km à pied en courant à |
|
|
|
Un
train part de Paris à 10 heures vers Bordeaux, éloignée de Un
second train part de Poitier à 11 h 25
minutes vers Bordeaux , éloignée de |
|
|
|
Les
villes de Lyon et de Paris sont
séparées de |
|
|
|
Une grand rue a une longueur de |
|
|
|
Un
automobiliste met 8 heures pour aller
de Paris à Monpellier. Sachant que la distance
entre ces deux villes est de |
|
Vitesse
moyenne :
|
|
Un représentant de commerce à domicile a
parcouru |
|
|
|
Un
randonneur effectue : |
|
|
|
Un
cycliste parcourt : Puis
Et puis
Quelle
est sa vitesse moyenne ?. |
|