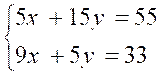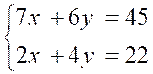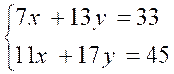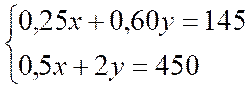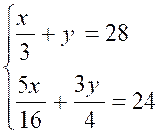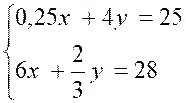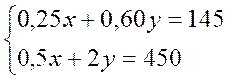|
|
|
DOC : Formation Individualisée |
DOC : Elève. |
|
ALGEBRE.
N° 29 |
Information « TRAVAUX » ;Cliquer sur
le mot !. |
|
OBJECTIFS :- médiation en algèbre. |
I ) Pré requis:
|
i9 |
Le calcul numérique |
:i |
|
i9 |
Liste des objectifs « passerelle » 3ème /
Seconde. |
:i |
|
i9 |
:i |
II ) ENVIRONNEMENT du dossier :
|
Dossier suivant : 30 Difficultés
pour résoudre un système par la méthode précédente. |
Info n°1 : résoudre une équation. |
Problèmes à 2
inconnues.
Système de deux
équations du premier degré à deux inconnues.
Méthode
de résolution dit « par addition » ou dit « par
soustraction ».
IV) INFORMATIONS
« formation leçon » :
|
|
Travaux auto - formation. |
|
Corrigé des
travaux auto - formation. |
|||
V ) DEVOIRS
( écrits):
|
Devoir diagnostique L tests. |
|
|
Devoir
Auto - formatif (intégré
au cours) |
|
|
Devoir Formatif « Contrôle :
savoir » ; (remédiation) |
|
|
|
|
|
Devoir sommatif. |
|
|
Devoir
certificatif : (remédiation) |
|
*
remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour
conclure une formation .
|
Leçon |
Titre |
|
N°29 |
Problèmes à 2 inconnues. |
|
INTERDISCIPLINARITE : Problèmes à 2 inconnues. |
|
Pierre
a acheté 6 lecteurs lasers et 5 lecteur MP3 pour 270 euros. Paul a acheté 4
lecteurs et 2 lecteurs MP3 pour 140 euros. Quels étaient les prix
respectifs d’un lecteur laser et d’un
lecteur MP3.
I)
mise en équation :
On
demande 2 prix. Il y a donc 2 inconnues.
Représentons
par « x » le prix du lecteur et par « y » celui de la
radio.
On
peut écrire :
Premier
achat : 6x + 5y = 270 (1)
Deuxième
achat 4x + 2y = 140 (2)
Ce
qui est représenté par l’écriture : 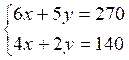
Cette
écriture représente un système
appelé « système de deux
équations à deux inconnues »
Remarque : Quand il y a plusieurs
inconnues, on peut les calculer à condition qu’on dispose d’autant d’équations
que d’inconnues.
II)
Calcul des inconnues par une
première méthode.
Multiplions par
« 2 » les deux membres
de (1) 12 x + 10y = 540
Multiplions par
« 3 » les deux membres
de (2) 12 x + 6y
= 420
![]()
Retranchons membre à membre 0 x + 4 y
= 120
Cela revient à retrancher 2
quantités égales aux deux membres de la première égalité.
D’ où 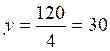
Portons la valeur de
« y » dans l’équation (1) 6x +
5y = 270
Ce qui donne 6x + 150 = 270
D’où 6x = 270 - 150
6 x = 120
Et 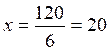
Conclusion Nous avons donc :
x = 20 euros , ce qui donne le prix du lecteur
laser .
y = 30 euros , ce qui donne le prix du lecteur MP3
III) Vérification.
Remplaçons
« x » par « 20 »
et « y » par « 30 » dans le système, on a :
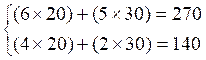
Ce qui vérifie les égalités.
Procédure à utiliser
pour résoudre un problème à deux inconnues :
dans un problème qui contient 2 inconnues.
- On écrit les 2 équations qui
fournissent l’interprétation de l’énoncé.
- On fait les multiplications
nécessaires pour obtenir 2 équations ayant un terme identique
- On soustrait membre à membre ces
2 équations.
- On tire la valeur d’une inconnue.
- On porte cette valeur dans une
des équations du premier système .
- On calcule la valeur de la
deuxième inconnue.
I)
|
Titre |
|
|
N°29 |
TRAVAUX d’Auto - FORMATION sur Problèmes
à 2 inconnues. |
Donner la procédure à utiliser
pour résoudre un problème à deux inconnues
Résoudre :
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
1°)
Une maison est vendue et le vendeur en profite pour lever une hypothèque qui
couvrait le 1/3 du prix de vente. Il vend ensuite une terre et lève une deuxième hypothèque qui couvrait
le 1/5 du prix de cette nouvelle vente.
Les
deux ventes ont produit 85 000 euros et les deux hypothèques s’élevaient à
25 000 euros. Calculer les prix de vente de chacune des deux propriétés?
CORRIGE :
Résoudre :
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
Problème :
1°) Une maison est vendue et le vendeur en profite pour lever
une hypothèque qui couvrait le 1/3 du prix de vente. Il vend ensuite une terre et lève une deuxième hypothèque qui couvrait
le 1/5 du prix de cette nouvelle vente.
Les deux ventes ont produit 85 000 euros et les deux
hypothèques s’élevaient à 25 000 euros. Calculer les prix de vente de
chacune des deux propriétés?