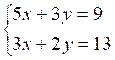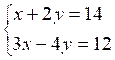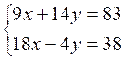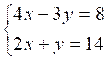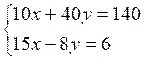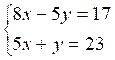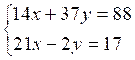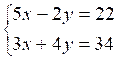@

Devoir diagnostique L tests.	
Devoir Auto - formatif (intégré au cours)	
Devoir Formatif « Contrôle : savoir » ; (remédiation)	
Devoir Formatif « Evaluation savoir faire » (remédiation)	
Devoir sommatif.	
Devoir certificatif : (remédiation)	

* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .

Leçon

Titre

N°30

Système de deux équations du premier degré à deux inconnues

Problèmes à 2 inconnues : Méthode par « addition » ou « soustractions » ; difficultés rencontrées.

COURS sur :

INTERDISCIPLINARITE : Problèmes à 2 inconnues : Méthode par « addition » ou « soustractions » ; difficultés rencontrées.

I) Principes fondamentaux.

1°) Considérons l’expression algébrique « a+b -c ».

« a » et « b » sont précédés du signe + . On les appelle « termes positifs ».

« c » est précédé du signe « - » . On l’appelle « terme négatif ».

2°) Nous avons vu ( leçon12) que lorsqu’on additionne les termes d’une parenthèse, ces termes qui étaient contenus dans ces parenthèses conservent leur signe.

Exemple : a + ( b - c) = a + b - c

Ainsi en ajoutant « b » , nous avons obtenu « +b »

En ajoutant « -c » nous avons obtenu « -c »

On retiendra :

Pour additionner un terme positif, on ajoute le terme.

Pour additionner un terme négatif, on retranche le terme.

3°) De même, nous avons vu que lorsqu’on soustrait les termes d’une parenthèse , ces termes changent de signe.

Exemple : a - ( b - c) = a - b + c

Ainsi en retranchant « b » , nous avons obtenu « -b »

En retranchant « -c » nous avons obtenu « +c »

On retiendra :

Pour soustraire un terme positif, on retranche le terme.

Pour soustraire un terme négatif, on ajoute le terme.

II) Première difficulté de résolution.

Soit résoudre le système :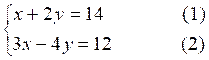

On décide de multiplier par « 2 » les 2 membres de l’équation (1) et conserver (2) :

2x + 4y = 28

3x - 4 y = 12

On additionne : 5x + 0 y = 40

Pour ajouter (-4), nous avons retranché 4y.

D ‘ où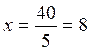

Portons cette valeur dans (1) : 8 + 2y = 14

Soit 2y = 6

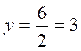
Remarque : Pour annuler deux termes identiques mais de signe contraire, (quand l’un est négatif et l’autre positif), il faut procéder par addition. Pour ajouter un terme négatif, il suffit de soustraire le terme.

III) Deuxième difficulté de résolution.

Soit à résoudre le système :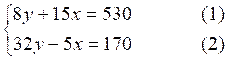

On multiplie par «4 » les deux membres de l’équation (1) , on ne modifie pas l’équation (2)

On a : 32 y + 60 x = 2 120

32 y - 5 x = 170

Retranchons : 0y + 65 x = 1950

Remarque : pour retrancher « -5 x », nous avons ajouter « 5 x »

D’où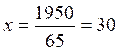

Recherche de « y » :

Portons cette valeur dans l’équation (2) :

32 y - 5 x = 170 ; soit 32 y = 170 + 5x

32 y = 170 + 5´ 30

32 y = 170 + 150

32 y = 320

d’ où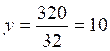

Faire la vérification !!!!!

Remarque : Quand on procède par soustraction, on rencontre parfois des termes négatifs à soustraire. Pour soustraire un terme négatif, on ajoute ce terme.

Leçon

Titre

N°30

TRAVAUX d’Auto - FORMATION sur

Problèmes à 2 inconnues : Méthode par « addition » ou « soustractions » ; difficultés rencontrées.

TRAVAUX N° 30 d ’ AUTO - FORMATION : CONTROLE

Compléter les phrases suivantes :

1°) Pour annuler deux termes identiques mais de signe contraire, (quand l’un est négatif et l’autre positif) , il faut procéder par ……………... Pour ajouter un terme négatif, il suffit de ……………… le terme.

2°) Quand on procède par soustraction, on rencontre parfois des termes négatifs à soustraire. Pour soustraire un terme négatif, on …………….. ce terme.

TRAVAUX N°30 d ‘ AUTO - FORMATION EVALUATION

Résoudre :

1
2
3
4
5
6
7
8

Problème :

1°) Un marchant tailleur prend chez son fournisseur 15 m de drap et 8 m de toile . IL paye 530 euros. Une autre fois, il prend 32 m de toile et rend 5 m de drap et paye 170 euros. Trouver les prix au mètre de toile et mètre de drap.

CORRIGE :

Résoudre :

1
2
3
4
5
6
7
8

Problème :

1°) Un marchant tailleur prend chez son fournisseur 15 m de drap et 8 m de toile. IL paye 530 euros. Une autre fois, il prend 32 m de toile et rend 5 m de drap et paye 170 euros. Trouver les prix au mètre de toile et mètre de drap.