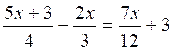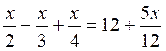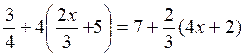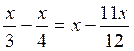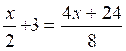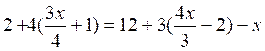Index warmaths

Liste des leçons

DOC. : Professeur ; Formateur

DOC : Formation Individualisée

DOC : Elève.

ALGEBRE. N° 27

Information « TRAVAUX » Cliquer sur le mot !.

INFORMATIONS PEDAGOGIQUES :

NIVEAU :Formation Niveau V (inclus le CAP et CFA)

OBJECTIFS :- médiation en algèbre.

I ) Pré requis:

i9	Le calcul numérique	:i
i9	Liste des objectifs « passerelle » 3^ème / Seconde.	:i
i9	Liste des leçons	:i

II ) ENVIRONNEMENT du dossier :

Index

Dossier précédent  26:

Dossier suivant : 28 Problème d’application.

Info n°1 : résoudre une équation.

III ) LECON n°27 : Impossibilité et indétermination.

IV) INFORMATIONS «  formation leçon » :

Test	COURS	Travaux auto - formation.			Corrigé des travaux auto - formation.
		Contrôle	évaluation	INTERDISCIPLINARITE	Corrigé Contrôle	Corrigé évaluation

V ) DEVOIRS ( écrits):

Devoir diagnostique L tests.	
Devoir Auto - formatif (intégré au cours)	
Devoir Formatif « Contrôle : savoir » ; (remédiation)	
Devoir Formatif «  Evaluation  savoir faire » (remédiation)	
Devoir sommatif.	
Devoir certificatif : (remédiation)	

* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .

Leçon	Titre
N°27	Impossibilité et indétermination

COURS sur : Impossibilité et indétermination

Info plus

La résolution d’une équation parfois à deux cas déroutants :

I) Equation impossible.

Soit à résoudre :

2(x + 3) + 5 (x - 7) = 4 (2x + 5) - x

on développe : 2x + 6 + 5x - 35 = 8x + 20 - x

On regroupe les « x » dans le premier membre :

2x -8x + x +5x = 20 +35 - 6

Soit 0x = 49

Il n’y a pas de valeur de « x » qui, multipliée par « 0 », donne « 49 »

On dit que l’équation est impossible.

II) Equation indéterminée.

Soit à résoudre 4(x - 2) + 3(x - 5) = 5 (x - 3) + 2 ( x - 4)

On effectue : 4x - 8 + 3x - 15 = 5 x - 15 + 2 x - 8

Rassemblons les « x » dans le premier membre :

4x - 5 x - 2x + 3x = - 15 - 8 + 8 + 15

en réduisant 0x = 0

Une valeur quelconque de « x » multipliée par zéro donne zéro.

Prenons par exemple « x= 5 et portons cette valeur dans l’équation donnée :

4(5 - 2) + 3(5 - 5) = 5 (5 - 3) + 2 ( 5 - 4)

20 - 8 + 15 - 15 = 25 - 15 + 10 -8

12 = 12

Dans ce cas , on dit que l’ équation est « indéterminée »

III) Conclusion :

Une équation est impossible quand le coefficient de l’inconnue est nul et que le terme connu ne l’est pas.

Une équation est indéterminée quand le coefficient de l’inconnue et le terme connu sont nuls tous les deux.

IV)

Leçon	Titre
N°27	TRAVAUX d’Auto - FORMATION sur Impossibilité et indétermination

TRAVAUX N° 27 d ’ AUTO - FORMATION : CONTROLE

Compléter les phrases suivantes. :

1°) Une équation est impossible quand ………………………………………………….........................................

2°) Une équation est indéterminée

………………………………………………….........................................

TRAVAUX N°27 d ‘ AUTO - FORMATION EVALUATION

Série 1 : résoudre et conclure

1°) 2(x + 3) + 5 (x - 7) = 4 (2x + 5) - x

2°) 4(x - 2) + 3(x - 5) = 5 (x - 3) + 2 ( x - 4)

Série 2 : Résoudre :

1.	3(x - 4) + 5 ( x + 3) = 4(2x + 3)
2.
3.
4.	5 + 3x - 12 + 4(2 + x) = 7 (x +5)-3
5.
6.	5 ( x + 2) + 3( x - 2) = 4 ( 2x + 1)
7.	4x + 3 ( 4 + 2x) = 5 ( 2x +3) - 3
8.

9.
10.

Problème :

Voir les problèmes d’application , objectif suivant.

CORRIGE :

1°) :

1	A
2	B
3	C
4	D
5	E

Problème ^