LECON N°22	Devoir : Ÿ Remédiation : Ÿ	Nom :…………	Classe : Groupe :
Date :……………	Rattrapage : Ÿ Soutien : Ÿ	Prénom :…………	Note contrôle :	Note évaluation :

CORRIGE :	Exercices cours  :
N°22	RELATIONS TRIGONOMETRIQUES dans le Triangle Rectangle .

Résumé du COURS

CORRIGE :

CONTROLE:

1°) Donner la définition du sinus ; cosinus ; tangente d’un angle dans un triangle rectangle.

2°) Soit un triangle rectangle ABC , rectangle en A , B étant l’angle le plus aigu .

Etablir toutes les relations trigonométriques .

EVALUATION:

Série 1 :

1°) En utilisant la calculatrice ( Donner le résultat arrondi à 0,000 1 près )

( a :lire angle alpha )

Angle a	7,5°	15,5°	18,25°	26,75°	59,6°	59,8°	73°
Sin a
Cos a
Tan a

2°) En utilisant la calculatrice , compléter le tableau ( arrondir à 0,1 près )

	sina = 0 ,964	sina= 0,6435	sina =0, 1687
L’angle a est égal à

	Cos a = 0 ,913 4	Cos a= 0, 454 0	Cos a =0, 2968
L’angle a est égal à

	Tan a = 0 ,213 4	tana= 1	Tan a =45, 1187
L’angle a est égal à			88,7°

Série 2 :Calculs 

I ) Soit un triangle CBA rectangle en B .l’angle A = 67° et [ A B] = 30 cm.

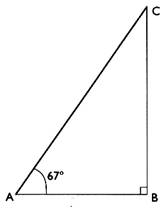
Question : on demande de calculer la longueur du côté [C A] .

II ) Soit un triangle CBA rectangle en B .l’angle A = 50° et [B A] = 25 cm.

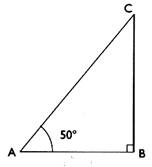
Question : on demande de calculer la longueur du côté [ B C] .

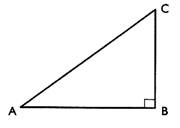
III) Calculer la valeur de l’angle A , en degré .

[AC] = 54 mm et [ AB] = 35 mm

.

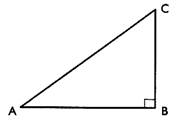
IV) Calculer la valeur de l’angle A , en degré .

[AC] = 54 mm et [ B C ] = 12 ,5 mm

.

IV) Calculer la valeur de l’angle A , en degré .

[AB] = 45 mm et [ B C ] = 12 ,5 mm

.

V) Dans un triangle ABC , rectangle en B , tel que AB = 10 cm et BC = 7cm. Calculer AC et la mesure de l’angle A . Sachant que la somme des trois angles d’un triangle est égale à 180° , en déduire la mesure de l’angle C .

VI) Dans un triangle rectangle EGF , rectangle en G, on donne : = 38° et FG = 100 mm.( FG étant le côté adjacent à l’angle F ).

-Dessiner le triangle à l’ échelle 1 .

- Calculer EG en utilisant la tangente.

- Calculer FE en utilisant le cosinus de .

VII ) Soit la figure ci dessous :

Dans un triangle ABC rectangle en B , on donne AB = 40 cm et = 35°.

Calculer BC et AC .

VIII) Soit la figure ci dessous :

Dans un triangle ABC rectangle en B , on donne AB = 13 cm et = 65°.

Calculer BC et AC .

PROBLEMES :

1°) ( à mettre en relation avec le coefficient directeur d’une droite dans la représentation graphique de la fonction affine et linéaire)

( remarque : la fonction linéaire est un cas particulier de la fonction affine)

Sur la droite « D » de la figure ci -dessous , placer le point « B » à 5 cm de « A » . Construire un triangle rectangle ABC ayant pour hypoténuse le segment [AB]

et un côté de l’angle droit parallèle à ( D’) .

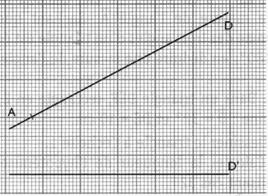
Mesurer sur la figure les longueurs des côtés de l’angle droit et calculer la tangente de l’angle . En déduire la mesure de cet angle ( en degré ).

Quel est l’angle formé par les droites D et D’ ?

On a ainsi trouvé l’angle des deux droite sans utiliser le rapporteur .