@

DOSSIER : N°22:       

Leçon

Titre

N°22

CORRIGE : 

LES  RELATIONS  TRIGONOMETRIQUES  dans le triangle rectangle .

 

CONTROLE:

 

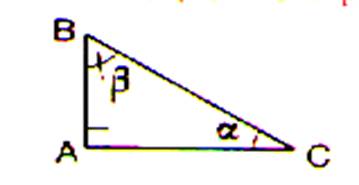
1°) Les angles ( désignations) .

Mots à placer : AC.  ( ou CA ) ;  l’angle droit ; côté adjacent   ; Bêta ; alpha ; AB  ( ou BA ) ; consécutifs.

 

Pour le symbole « b » lire « bêta »

Pour le symbole « a »  lire « alpha »

En « A » : un carré (ou rectangle) symbolise l’angle droit.

 

L’angle  « b » se trouve   à l’opposé  du côté AC.  ( ou CA )

L’angle  « a »  se trouve  à l’opposé du  côté AB  ( ou BA )

Les côté AB et BC sont consécutifs . ( AB est appelé le « côté adjacent » à l’angle « b »)

Les côtés AC et CB sont consécutifs. ( AC est appelé le « côté adjacent » à l’angle « a »)

 

 

 

2°) Identification du « Côté opposé » , « côté adjacent » , « hypoténuse » d’un angle

Pour un triangle rectangle CBA ; rectangle en B :nommer  les côtés :

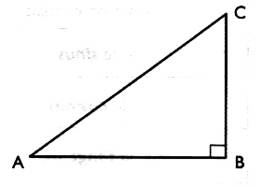
Compléter le tableau suivant avec les mots : Côté  opposé   ( à ) ; Côté adjacent (à ) ; côté adjacent  à 90° ; Hypoténuse ; Côté adjacent   ( à ) ; Côté opposé  ( à )

 

 

Si l’on se fixe sur un angle ; on nommera les côtés  de la façon suivante :

 

Pour l’angle droit

Pour l’angle    

Pour l’angle    

AC

est appelé :

Côté opposé à 90° :   Hypoténuse

Hypoténuse

Hypoténuse

AB

est appelé

côté adjacent  à 90°

Côté adjacent (à )

Côté  opposé   ( à )

BC

est appelé

côté adjacent  à 90°

Côté opposé  ( à )

Côté adjacent   ( à )

 

3°)citer  les 3 principales relations trigonométriques sur le sinus , cosinus , tangente  ; donner le modèle  symbolique  mathématique.

 

a)  Sinus d’un angle aigu : Le sinus d’un angle ( noté : sin. ) est un nombre égal au quotient du rapport de la longueur du côté opposé à cet angle sur la longueur de l’hypoténuse .   

Sin.  =

 

b)  Cosinus d’un angle aigu : Le cosinus d’un angle ( noté : cos. ) est un nombre égal au quotient du rapport de la longueur du côté adjacent  à cet angle sur la longueur de l’hypoténuse .      cos. =

 

c) La tangente d’un angle aigu : La tangente d’un angle ( noté : tan. ) est un nombre égal au quotient du rapport de la longueur du côté opposé à cet angle sur la longueur du côté adjacent à cet angle .

tan. =

 

4°)  Appliquer au triangle rectangle  ACB   les relations précédentes :

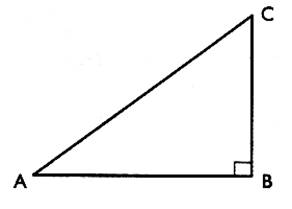
A quel rapport est égal ? :

 ;  ;      ;   ;  ;

 

 

- Dans le triangle rectangle  CBA , rectangle en B , on aura les égalités suivantes :

-          ;  ;

 

 

-          ;  ;

 

5°) Passage d’une valeur décimale d’un sin a; cos a, tan a, à la valeur en degré de l’angle a

Compléter les phrases suivantes :avec les mots : en degré ; valeur décimale .

Lorsque l’on connaît la valeur décimale du sinus , du cosinus ou de la tangente d’un angle ,en consultant une table numérique  ou une calculatrice scientifique  obtenir  la valeur en degré de cet  angle .

Inversement si je connais la valeur en degré de l’angle je peux obtenir avec la table numérique ou la calculatrice la valeur décimale du sinus , cosinus ou  tangente de cet  angle .Le chapitre suivant aborde ce travail.

 

6°)    Détermination de la valeur décimale d’un sinus , cosinus et tangente à partir de la valeur  en degré de l’angle aigu.

Les valeurs des rapports trigonométriques ( sinus , cosinus , tangente ) d’un angle aigu sont données par la calculatrice , ou une table numérique.

Sur une calculatrice , les angles peuvent être exprimés en degrés décimaux , grades ou radians .

L’unité d’angle utilisé couramment  est le degré décimal.

7°) pour des calculs en trigonométrie il faut  mettre la calculatrice en mode  DEGRE 

8°)  Compléter le tableau ( voir votre calculatrice)

 

 

Pour trouver le sinus d’un angle aigu

Introduire  la mesure de l’angle  ( en degré)

Puis presser sur la touche

  «  SIN »

Pour trouver le cosinus d’un angle aigu

Introduire  la mesure de l’angle  ( en degré)

Puis presser sur la touche

  «  COS »

Pour trouver la tangente sinus d’un angle aigu

Introduire  la mesure de l’angle  ( en degré)

Puis presser sur la touche

  «  TAN »

 

7°) mettre la calculatrice en mode  DEGRE

Détermination de la valeur de l’angle  en degré connaissant la valeur du sinus ou cosinus ou tangente avec la calculatrice :

Donner la touche remplissant la même fonction  sur votre calculatrice  :

    A partir de la  valeur décimale « sinus »  pour obtenir la valeur en degré  appuyer sur la touche :   INV . SIN ; ou  SIN-1 ; ou ASN ; 

 A partir de la  valeur décimale « cosinus »  pour obtenir la valeur en degré  appuyer sur la touche  INV . COS ; ou  COS-1 ; ou ACN ; 

 A partir de la  valeur décimale « tangente »  pour obtenir la valeur en degré  appuyer sur la touche  INV . TAN ; ou  TAN-1 ; ou ATN ; 

 

8°)Utiliser la calculatrice  pour trouver l’angle C dont le sinus est 0,876 5 , l’angle  A dont le cosinus est 0,423 6  et l’angle  C dont la tangente  est 1,973 2

Solution :

-  sinus 0,876 5  =  61,22 30002674563870029460466444187°  » 61,22° ; l’angle A » 61,22° 

- cosinus 0,423 6 = 64,9379198941684120820136530194404    » 64,94 ° ; l’angle B » 64,94 ° 

- tangente 1,9732 =63,1245186381872560194775281181102    » 63,12° ; l’angle C » 63,12 °

 

 

 9 °) Compléter les phrases suivantes   sur les Calculs d’éléments d’un triangle rectangle :

avec les mots :  180° ; aigus ; Pythagore ; complémentaires ;( somme des 2 angles aigus) .

 

Dans un triangle rectangle si l’on connaît 2 côtés on peut avec « Pythagore » trouver la longueur du troisième coté . La somme des angles dans un triangle est de 180° . La somme dans un triangle rectangle est de  180° = 90° + ( somme des 2 angles aigus) .

(ces deux angles aigus ,dont leur somme est de 90°, sont appelés : angles complémentaires)

Dans un triangle rectangle , si je connais la longueur  de deux côtés , j’applique  « Pythagore » pour trouver la longueur du troisième côté.

Dans un triangle rectangle , si je connais la longueur  de deux côtés , je peux calculer  le sinus ou  le cosinus ou la tangente  pour trouver la valeur d’un des angles aigus .

 

EVALUATION:  

1 °) Utiliser la calculatrice pour trouver le sinus , cosinus et tangente des angles : 7° ; 30° ; 84°.

Angle :

Sinus

Cosinus

Tangente

7°

0,12186934340514

0,99254615164132

0,12278456090290

30°

0,5

0,86602540378443

0,57735026918962

84°

0,99452189536827

0,10452846326765

9,51436445422258

( en général on arrondit au 0,001 près )

 2°)Utiliser la calculatrice  pour trouver l’angle C dont le sinus est 0,876 5 , l’angle  A dont le cosinus est 0,423 6  et l’angle  C dont la tangente  est 1,973 2

Solution :

-  sinus 0,876 5  =  61,22 30002674563870029460466444187°  » 61,22° ; l’angle A » 61,22° 

- cosinus 0,423 6 = 64,9379198941684120820136530194404    » 64,94 ° ; l’angle B » 64,94 ° 

- tangente 1,9732 =63,1245186381872560194775281181102    » 63,12° ; l’angle C » 63,12 °

3°) En utilisant la calculatrice  ( donner le résultat arrondit à  0,000 1 près )

( a :lire angle alpha )

Angle a

0°

15°

30°

45°

60°

75°

90°

Sin a

0

0,2588

0,5

0,7071

0,8660

0,9659

1

Cos a

1

0,9659

0,8660

0,7071

0,5

0,2588

0

Tan a

0

0,2679

0,5774

1

1,7320

3,7321

Infini.

 

4°) En utilisant la calculatrice , compléter le tableau ( arrondir à 0,1 près )

 

sina = 0 ,213 4

 sina= 0,54 00

sina =0, 9687

L’angle a est égal à

12,3°

32,7°

75,6°

 

 

Cos a = 0 ,213 4

 Cos a= 0,54 00

Cos a =0, 9687

L’angle a est égal à

77,7°

53,1°

14,4°

 

 

Tan a = 5 ,213 4

 Tan a = 1

Tan a = 0, 1187

L’angle a est égal à

79,1°

45°

6,8°

 

 

 

 

 

 

 

Utilisation  de  table   de trigonométrie .

 

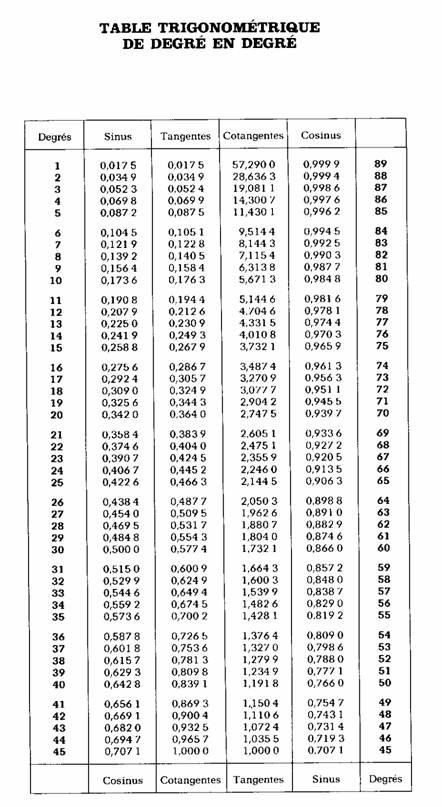
3 °) « SINUS d’un angle »  :

 

A )Recherche du sinus à partir d’un angle

Avec la table.

Avec la calculatrice scientifique

1°

0,0175

0,17452406

10°

0,1736

0,1736481777

24°

0,4067

0,406736643

30°

0,500000

0,50000000

45°

0,7071

0,707106781

60°

0,8660

0,866025404

90°

1

1

 

B ) Recherche d’ un angle à partir d’un nombre décimal (n £ 1 )

Avec la table.

Avec la calculatrice scientifique

0,2419

14 °

Forme décimale :

13,99870707

forme sexagésimale :

13°59’55’’35/100

0,8290

56°

55,99615045

55°59’46’’14 /100

0,289256198

16°30’

16°48’48’’35/100

0,5

30°

 

0,866

59,99708907°

59°59’49’’

 

4°) « COSINUS d’un angle »  :

 

A )Recherche du cosinus à partir d’un angle

Avec la table.

Avec la calculatrice scientifique

1°

0,9999

0,999847695156391239157011558813915

10°

0,9848

0,984807753012208059366743024589523

24°

0,9135

0,913545457642600895502127571985317

30°

0,8660

0,866025403784438646763723170752936

45°

0,7071

0,707106781186547524400844362104849

60°

0,5000

0,5

90°

0

0

 

B ) Recherche d’ un angle à partir d’un nombre décimal (n £ 1 )

Avec la table.

Avec la calculatrice scientifique

0,2419

76

76,0012929273909452030608943275762

0,8290

34

34,0038495510334231386333849747562

0,289256198

73

73,1865690727659438937455877084968

0,5

60°

60°

0,866

30)

30,0029109311880257827344380174439

 

5° ) « Tangente d’un angle »  :

 

A )Recherche d’une tangente à partir d’un angle

Avec la table.

Avec la calculatrice scientifique

1°

0,0175

0,0174550649282175857651288952197278

10°

0,1763

0,176326980708464973471090386868619

24°

0,4452

0,445228685308536163922367030645666

30°

0,5774

0,577350269189625764509148780501957

45°

1,0000

1,000

60°

1,7321

1,73205080756887729352744634150587

90°

Infini

Infini

 

B) Recherche d’ un angle à partir d’un nombre décimal

Avec la table.

Avec la calculatrice scientifique

0,2419

Entre 13 et 14°

13,598621846296300005000876844386

0,8290

Entre 39 et 40°

39,6587315648276904009258333961383

0,289256198

16°

16,1328405121331118923472311358334

0,5

Entre 26 et 27°

26,5650511770779893515721937204533

0,866

Presque 41°

40,8925629074563470010890415264752

1

45°

45°

12,56

Entre 85 et 86 °

85,4478366300075891173256624914393

19

87°

86,9872124958166600548819457850051

57,2900

89°

88,9984275643442281937830467049166

169

Entre 89 et 90°

89,6609756755485497756239006787162

5067

Presque 90°

89,9886923665345948266430392503244

12568

Presque 90°

89,9954411378586751730828079184392

 

6°) On donne la longueur de l’hypoténuse et la longueur d’un côté  d’un triangle rectangle.

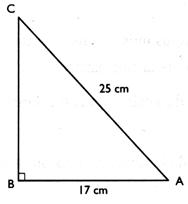
Que représente [CA ] et [BA] pour l’angle A ?.

Que représente [CA ] et [BA] pour l’angle C ?.

 

Solution :

Observations : our l’angle A :  le segment  CA  (  [CA] )est l’hypoténuse  , le segment BA  ( [BA]) est le côté adjacent. 

Pour l’angle C : le segment  CA  (  [CA] )est l’hypoténuse  , le segment BA  ( [BA]) est le côté opposé . 

Calculs :

a) On demande de trouver la valeur de l’angle A , en degré .

b) En utilisant les relations trigonométriques trouver la valeur en degré de l’angle C.

Remarque : calculer la somme des angles   +    

Vérifier que  la somme des angles dans un triangle  est égale  à 180°

 

Solution :

a)    Calcul de la valeur de l’angle A , en degré .

.

Procédure :

Solution :

1°)inventaire des données :

[CA] est l’hypoténuse , [BA] est le côté adjacent à l’angle A

[CA ] =  25 cm   et  [BA]= 17 cm

 

2°) Etablissement des formules :

( à partir des 3 définitions) 

Sin A = ;cos A =   ; tan =   

Analyse :La relation trigonométrique  « cosinus »  est la seule  formule utilisable avec les données .,

cos A =   

3°) calcul du  cos A =   

cos A =   ; cos A = 0,680 0

4°) Calculatrice : recherche de la valeur angulaire.

= 47,1563569564036622080449988396549

= 47,16°

(à vérifier sur un dessin à l’échelle )

 

 

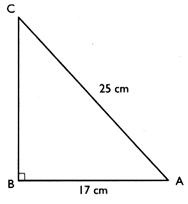
b) Calcul de la valeur de l’angle C , en degré .

 

.

Procédure :

Solution :

1°)inventaire des données :

[CA] est l’hypoténuse , [BA] est le côté adjacent à l’angle A

[CA ] =  25 cm   et  [BA]= 17 cm

 

2°) Etablissement des formules :

( à partir des 3 définitions) 

Sin C = ;cos C = ; tan C =    

Analyse :La relation trigonométrique  « cosinus »  est la seule  formule utilisable avec les données .,

Sin C =   

3°) calcul du  sin C =   

Sin C =   ; sin C  = 0,680 0

 

4°) Calculatrice : recherche de la valeur angulaire.

= 42,8436430435963377919550011603451

= 42,84°

(à vérifier sur un dessin à l’échelle )

Remarque : les angles  = 42,84°   et   = 47,16°  ont pour somme :

 42,84°  +  47,16°  = 90,00°  soit 90°

Ce qui vérifie que dans un triangle  la somme des angles est de :

90° + 42,84°  +  47,16° =  180° ;soit   90° + 90° = 180° 

 

 

 

 

 

 

 

 

 

7°)  Calcul de la longueur d’un côté  connaissant un angle et la longueur d’un autre côté .

      Soit un triangle CBA rectangle en B .

      On donne l’angle A  = 42°  et  [B A]  = 20 cm.

 

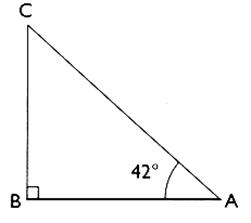
Question : on demande de calculer la longueur du côté [ B C]  .

Procédure :

Solution :

1°)inventaire des données :

 [BA] est le côté adjacent à l’angle A.

On obtient ,avec la calculatrice, la valeur décimale de :

Sin 42° : 0,669 1

Cos 42° : 0,743 1

Tan 42° :  0,9004

[BA ] =  20 cm   et    =  42 °

 

2°) Etablissement des formules :

( à partir des 3 définitions) 

 

Sin  = ;cos  = ; tan  =   

 

Analyse :La relation trigonométrique  « tan »  est la seule  formule utilisable avec les données . Il faut convertir tan 42° en valeur décimale avec la calculatrice . 

tan  =  

 

tan 42° = 0,900404044297839945120477203885372

3°) calcul de  CB  à partir de l’égalité : tan  =  ;  On remplace les lettres par les valeurs connues .

0,9004 =  

4°) transformation  ( produit en croix)

             =

20  0,9004 =  1  CB

CB = 18,00 cm

 

 

 

 

 

 

 

 

8°) :      Soit un triangle CBA rectangle en B .l’angle A  = 42°  et  [C A]  = 30 cm.

 

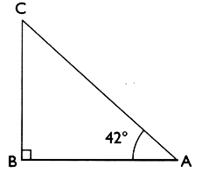
Question : on demande de calculer la longueur du côté [ B C]  .

 

Procédure :

Solution :

1°)inventaire des données :

 [CA] est l’hypoténuse du triangle .

On obtient ,avec la calculatrice, la valeur décimale de :

Sin 42° : 0,669 1

Cos 42° : 0,743 1

Tan 42° :  0,9004

[CA ] =  30 cm   et    =  42 °

 

2°) Etablissement des formules :

( à partir des 3 définitions)  , On cherche  CB .

Sin  = ;cos  = ; tan  =  

 

Analyse :La relation trigonométrique  « sin »  est la seule  formule utilisable avec les données . ( on connaît deux valeurs sur trois )

Sin  = 

 

3°) calcul de  CB  à partir de l’égalité : Sin  = ;  On remplace les lettres par les valeurs connues .

0,6691 =  

4°) transformation  ( produit en croix)

             =

30  0,6691 =  1  CB

CB = 20,07cm

 

 

9°)Dans le triangle rectangle ci - dessous : ( à vérifier par Pythagore )

 

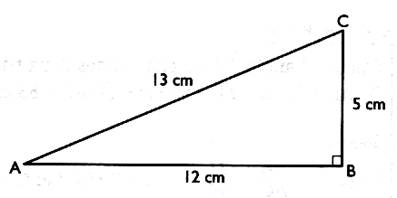
Calculer :   ;  ;   et puis  ,   et .

 

Solution :

 

 =

  =

 =

  » 0,384 6

»  0,923 1

 »  0 , 416 7

 

 » 0,384 6

  »  0,923 1

  »  0 , 416 7

 

 

 

»  0,923 1

  » 0,384 6

  = 2,4

 

 

  »  0,923 1

  » 0,384 6

  = 2,4

 

On remarque  que  :

-          »  0,384 6  et    » 0,384 6  , donc  …=…..   

 

 

-           »  0,923 1 et   »  0,923 1 ; donc   ……=….    

 

 

 

 

 

 

 

 

 

 

 

 

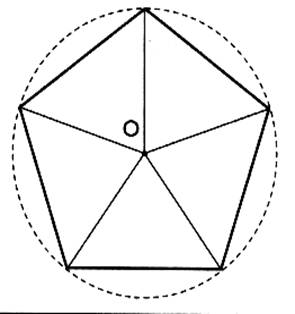
10°) On considère un pentagone  régulier inscrit dans un cercle de rayon 6 cm .

 a)Quelle est la nature  de chacun de ces cinq triangles dont le sommet  est le centre  "O" du cercle .  le triangle est un triangle isocèle  .(  360 ° / 5 =  72° )

b)Donner une mesure de chacun de leurs angles . ( rappel :la somme des angles d'un triangle est de 180 ° )  .  si l’angle au sommet 72° ; la somme des deux autres angles = 180 - 72° = 108 ° ; un angle de base =  108° :2 = 54°

c)Calculer l'aire de ce pentagone . ( pour calculer  "h"  la trigonométrie) .

Aire d’un triangle : il faut savoir calculer la hauteur « h » , distance qui va du centre à la base ? ( voir la trigonométrie )

Hypoténuse = 6 cm ; hauteur : sinus 54°  = 0,809  = h / 6 ; donc   h = 6 fois 0,809 = 4,85 cm ; base : cos 54° = 0,588  = b / 6  = 6 fois 0,588 = 3,53)

Un demi triangle : ( 4,85 fois  3,53  ) / 2 =  17,12 cm² ; il y a 10  demi - triangles équilatéral ; l’aire du pentagone =  17,12 fois 10 = 171,2 cm²