Leçon

TRAVAUX niveau V ; AUTO - FORMATIF  sur

N°16

LES SYMETRIES

·«  AXE de symétrie »  et   SYMETRIE CENTRALE ;

· « ORTHOGONALITE  » ,

· « CENTRE de symétrie »  et SYMETRIE ORTHOGONALE .

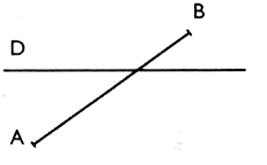
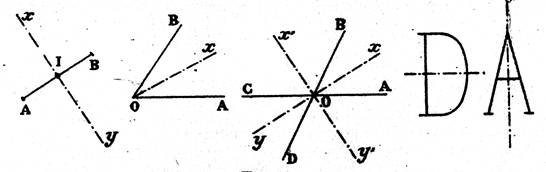
TRAVAUX  N°16    d ’ AUTO - FORMATION :  CONTROLE

1°) Nommer 2 droites qui sont "axe  de symétrie" .précisez ?

2°) Symétrie centrale :Compléter les phrases suivantes :

Par une symétrie centrale de ………….  "O" :

-          l'image d'un segment est ………………………………………. .

-          l'image d'un angle est …………………………….. .

-          l'image d'un polygone est ……………………………………...

-          L'image d'un cercle est ……………………………………….. .

La  symétrie centrale conserve ………………………………….. .

3°) Symétrie orthogonale  :Compléter les phrases suivantes :

Par une symétrie orthogonale ……………. ( D ) :

-          l'image d'un segment est ……………………………………… .

-          l'image d'un angle est un ……………………………………… .

-          l'image d'un polygone est ……………………………………….

-          L'image d'un cercle est ………………………………………… .

La  symétrie orthogonale  conserve ……………………………….. .

TRAVAUX N°16    d ‘ AUTO - FORMATION   EVALUATION

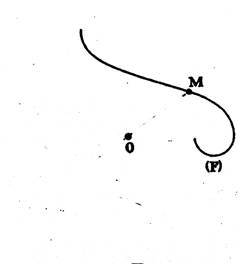
A)         Symétrie centrale :

1°) construire le symétrique de M par rapport à "O"

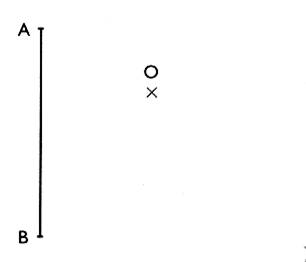
2°) construire le symétrique du segment AB  par rapport à "O"

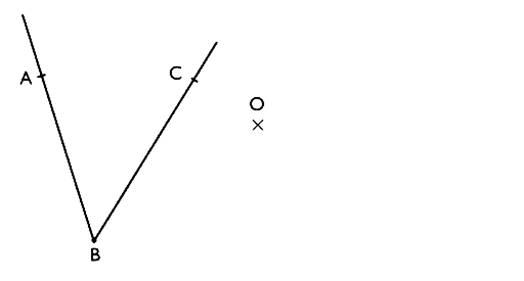
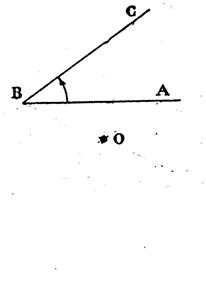
3°) Construire le symétrique de  l'angle    par rapport à "O"

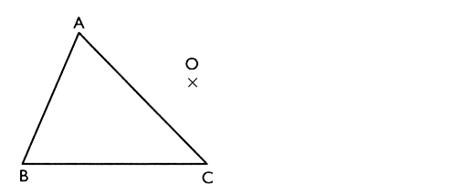
4°) construire le symétrique du polygone ( triangle)    par rapport à "O"

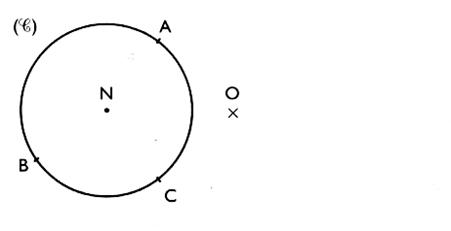
5°) construire le symétrique du cercle   par rapport à "O"

6°) tracer un segment [ A B ]  de  7 cm de longueur et placer un point O à une distance de 4 cm de la droite ( AB ) . Construire le symétrique  [ A' B' ] du segment AB par rapport à O . vérifier que le symétrique du milieu "N"  du segment AB  est le milieu N'  de  [ A' B '] . On dit que la symétrie  centrale conserve le milieu .

7°)

Tracé : dessiner cette figure sur une feuille  ( prendre une feuille de calque)

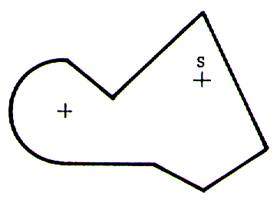
Dessiner avec la règle et le compas la symétrie de la figure ci-contre  de centre S .

Suite sur le CD :  pour en faire plus !!!!!

Symétrie centrale  ( cours 1)

Evaluation 2

Symétrie centrale   (cours 2 )

Evaluation 3

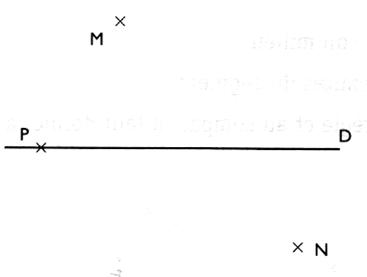
B ) Symétrie orthogonale :

1°)   Construire le symétrique orthogonal du point M , N et P .

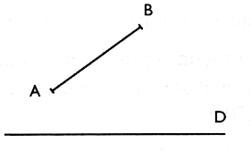
2°)  Construire le  symétrique orthogonale du  segment AB  , par rapport à la droite ( D ) .

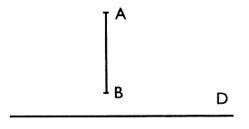
3°)    Construire le  symétrique orthogonale du  segment AB  , par rapport à la droite ( D ) .

3° )   Construire le  symétrique orthogonale du  segment AB  , par rapport à la droite ( D ) .

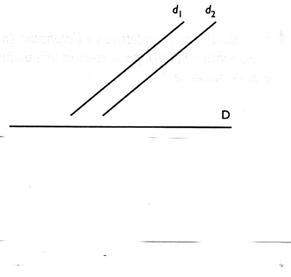
4°)Construire  les symétriques des droites ( d ₁ ) et ( d₂ ) parallèles par rapport  à la droite  ( D) .

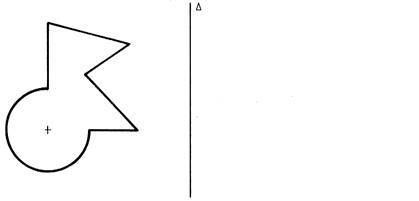
Dessiner la figure ci-dessous  dans la symétrie orthogonale d’axe  « delta » . Pour cela il faut déterminer l’image de certains points .

Laisser  les droites perpendiculaires à « delta » apparentes

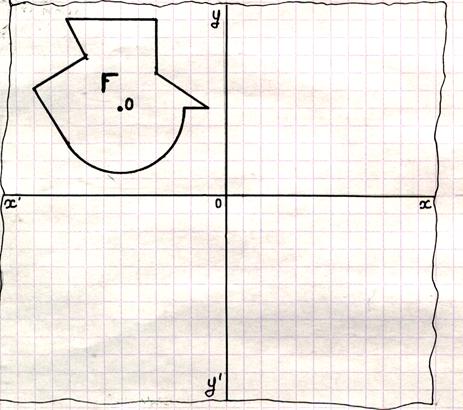
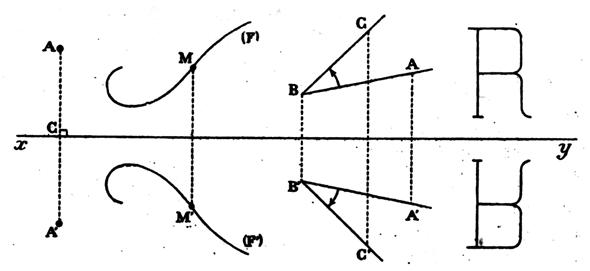
Synthèse  COMPOSITION de deux symétries orthogonales d’axes perpendiculaires.

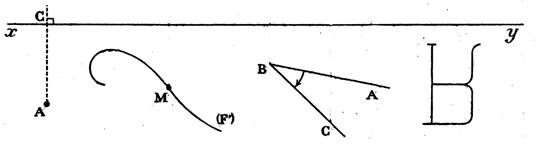
  xx’  et yy’ sont deux droites perpendiculaires sécantes en « O ».Dessiner l’image F’ de la figure  « F » dans la symétrie orthogonale d’axe x’x  puis l’image « F’’ » de la figure « F’ » dans la symétrie orthogonale d’axe yy’ .

INTERDISCIPLINARITE   Les symétries et applications .

1°) Tracer , s'ils existent , les axes de symétrie  de la  carte , ci - dessous : ( il ne faut pas tenir compte des chiffres )

2°) Tracer , s'ils existent , les axes de symétrie  de la  carte , ci - dessous : ( il ne faut pas tenir compte des chiffres )

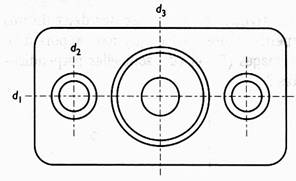
3°) Laquelle des droites  ( d₁) , d₂) et (d₃) n'est pas axe de symétrie de la pièce ci - dessous ?

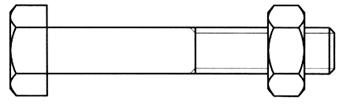
4°)Le dessin du boulon ci- dessous admet-il un  ( ou plusieurs ) axe (s) de symétrie ? et l'écrou seul ?

Expliquer pourquoi certains véhicules portent à l'avant  l'inscription :

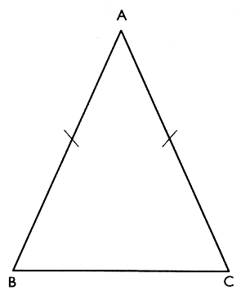
6°) Le triangle ABC est isocèle . Peut - on dire que la médiatrice du côté  AB est axe de symétrie  du triangle ?

Faire une figure . Prendre AB = AC = 5cm et  BC = 7 cm .

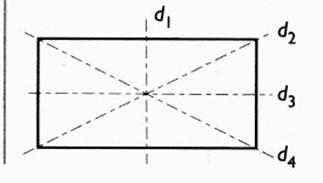
7°)    Laquelle des droites  ( d₁) , d₂) , (d₃) et ( d₄) n'est pas axe de symétrie du rectangle  ci - contre  ?

Si vous voulez plus d’exercices : CD 

Cliquer ici .

Regardez :

Tracer la symétrie orthogonale

Regarder :

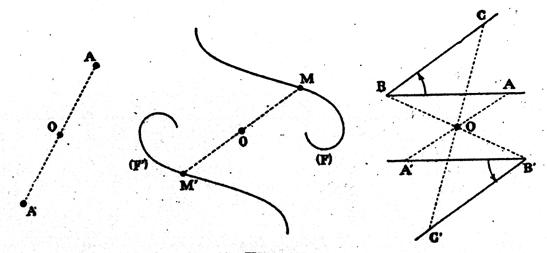
 Tracer la symétrie centrale de chaque figure , par rapport à « O »  :                                      

Info :  identifier   les axes de symétrie