|
Module : Géométrie
« dans l’espace ». |
DOSSIER :
147 |
||||||||||||
|
Warmaths ; Pour Aide et
Formation Individualisée
; REMEDIATION mise à /NIVEAU : niveau VI |
|||||||||||||
|
TRAVAUX NORMATIFS PRIMAIRE
/ COLLEGE Matière :
MATHEMATIQUES. Niveau VI_ V _ IV |
|||||||||||||
|
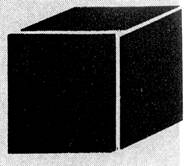
LE CUBE . Ses dimensions. |
|||||||||||||
|
|
|||||||||||||
|
Le
parallélépipède rectangle : Info
1 @ « cours sur le
parallélépipède rectangle … » ;
Info 2 @ « cours sur … » ; Info 3 @ « cours
sur … » |
|||||||||||||
|
Le
cube : Info 1 @ cours ;
Info 2 @ cours ;
Info 3 @ cours |
|||||||||||||
|
TRAVAUX
CONTROLE |
|||||||||||||
|
Les questions
relatives à « ce qu’il faut retenir » , au « savoir » se reporter aux cours
. |
|||||||||||||
|
LE CUBE ; ses surfaces |
|||||||||||||
|
|
Quand toutes les faces d’un parallélépipède rectangle sont des carrés , le parallélépipède
s’appelle « cube » Ses faces sont égales ; ses arêtes sont
égales. Dans toutes les positions possibles , la base ne
change pas, et la hauteur est toujours la même : c’est arête. |
||||||||||||
|
|
|||||||||||||
|
Activités. |
|||||||||||||
|
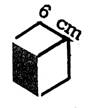
1
. Quelle longueur de ficelle emploie-t-on
pour les emballages ci-contre, le nœud
exigeant (pour
les deux cas ; l’arête du cube
mesure |
|||||||||||||
|
« A »
|
« B »
|
||||||||||||
|
2
. En utilisant |
|||||||||||||
|
« A »
|
« B »
|
||||||||||||
|
Développement :
|
|||||||||||||
|
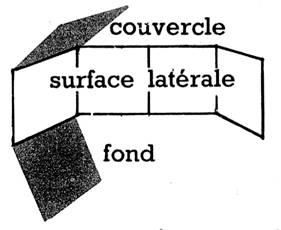
On
peut faire un cube en assemblant 6 carrés égaux; on peut le faire en pliant
et collant aux arêtes une forme comme la forme ci-dessous , appelée
développement du cube. La surface latérale est celle de 4 faces. La surface totale est celle des 6 faces 2
bases surface latérale. |
|||||||||||||
|
|
|
||||||||||||
|
|
|||||||||||||
|
3. Reproduire
et compléter ce tableau : Tableau
A |
|||||||||||||
|
arête du cube |
|
|
|
|
|
||||||||
|
surface d’une face ... |
……….. |
……….. |
……….. |
……….. |
……….. |
||||||||
|
surface totale |
……….. |
……….. |
……….. |
……….. |
………..……….. |
||||||||
|
#
# # Voir tableau B |
|||||||||||||
|
4. Calculez mentalement la
surface latérale d’un cube dont l’arête mesure 4cm; 5cm; 10cm; 20cm; 0,5m |
|||||||||||||
|
|
Développement du cube ! |
||||||||||||
|
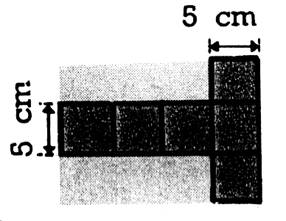
5. a) Trouvez les dimensions de la feuille dans
laquelle on découpe le développement
de cube ci-contre. b) Quelle est la surface totale du cube? c) Trouvez de deux façons la surface
inemployée de la feuille. |
|
||||||||||||
|
6.L’arête du cube B est
le double de celle cube A. a) Calculez la surface
totale du cube A. b) Calculez la surface totale du cube B. c) Comment auriez-vous pu trouver la surface totale du cube B en comparant
ses faces à celles du cube A? |
|||||||||||||
|
Cube A |
Cube B |
||||||||||||
|
|
|
||||||||||||
|
7
. Un peintre repeint,
extérieurement, les faces latérales des 8 caisses à fleurs de la devanture
d’un café. Chaque caisse est cubique et
mesure 8
. # # # ) Dans un cirque, les cubes sur lesquels grimpent les fauves ont sur
chaque face un cercle rouge touchant les arêtes; le reste est blanc. L’arête
mesure |
|||||||||||||
|
NIVEAU V
et IV :Reproduire et compléter ce
tableau : Tableau
B : ( # # # ) |
|||||
|
arête du cube |
……………. |
………… |
………… |
…………… |
|
|
surface d’une face ... |
64 cm² |
……….. |
……….. |
132,25 cm² |
900 cm² |
|
surface totale |
……….. |
24 cm² |
|
…………… |
………..…dm² |