Pré requis:
ENVIRONNEMENT du dossier:
|
Objectif précédent : Projection
d’un point sur une droite |
Objectif suivant : |
DOSSIER PROJECTION d ' un segment sur
une droite perpendiculaire à une
direction donnée.
Dit aussi :
« projection orthogonale »
|
|
|
Interdisciplinarité :
|
|
Corrigé Contrôle |
Corrigé évaluation |
Obj :
PROJECTE sur...
Voir définition du mot
« direction et sens ».
Mots utilisés dans
l’objectif : le vecteur
Préambule :
La
projection d ’
un point ; d’un segment (un ensemble
de points alignés) implique que l’on doit connaître (ou se fixer) :
n
une direction
(c’est une droite )
n
la position du point dans un plan ( en l’occurrence la feuille) et
n
la droite support qui recevra le
« projeté du point » .
Projection d’un point sur une droite:
Le
point A’ est le projeté du point A par rapport a la droite « d « ;
( le
segment de droite AA’ est parallèle à la droite
d ), sur la droite orientée « axe » .
La droite
d indique la ligne direction de
la projeté
d
A
A’
PROJECTION
ORTHOGONALE d’un point :
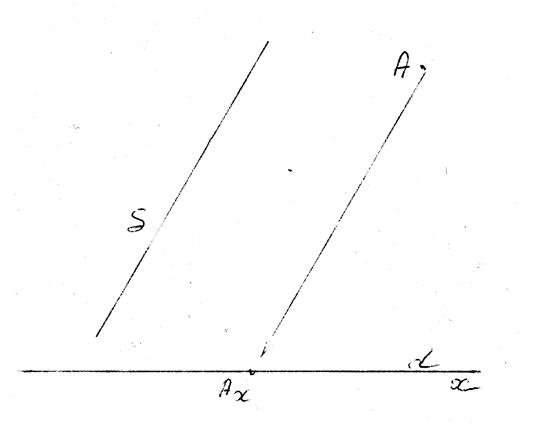
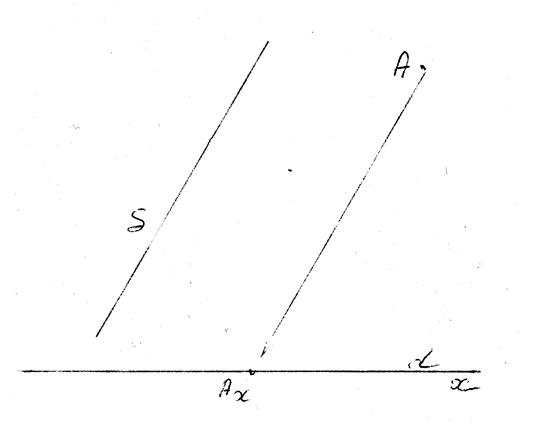
On fait la « projection
orthogonale »d’un point « M » lorsque la direction (delta) et la droite sur
laquelle on trace « la projetée du point « M’ » » sont
perpendiculaires
(utile pour :Obj : symétrie orthogonale)
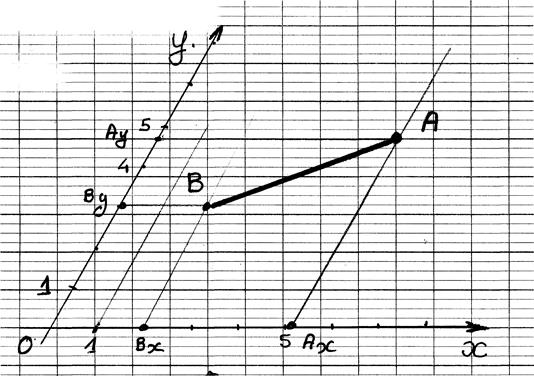
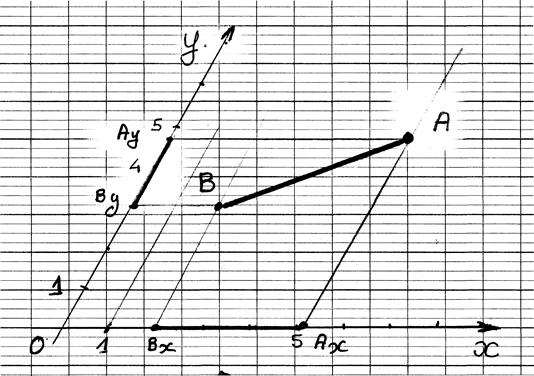
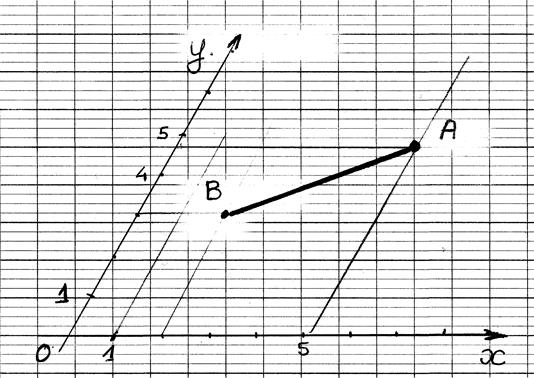
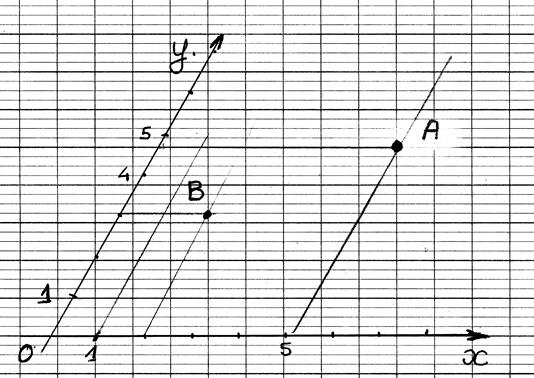
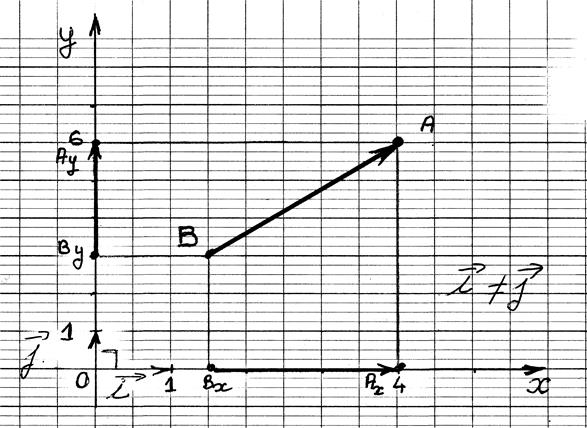
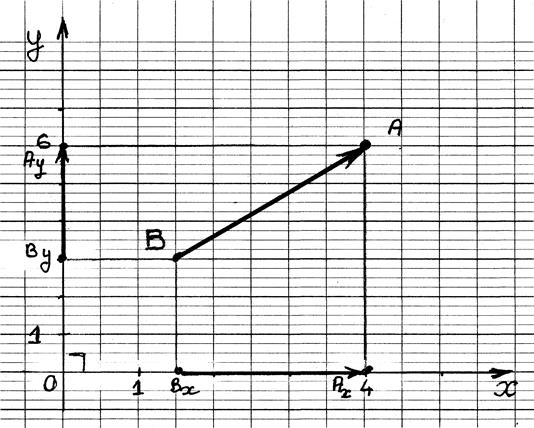
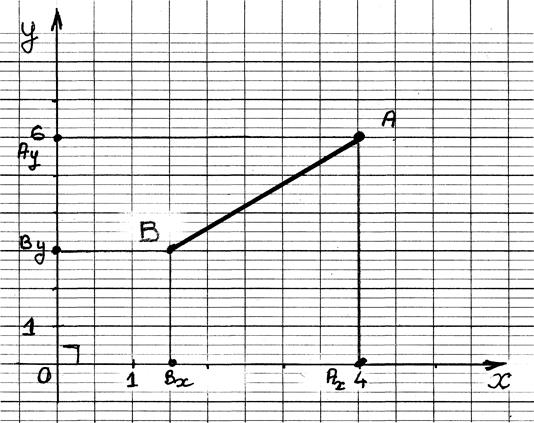
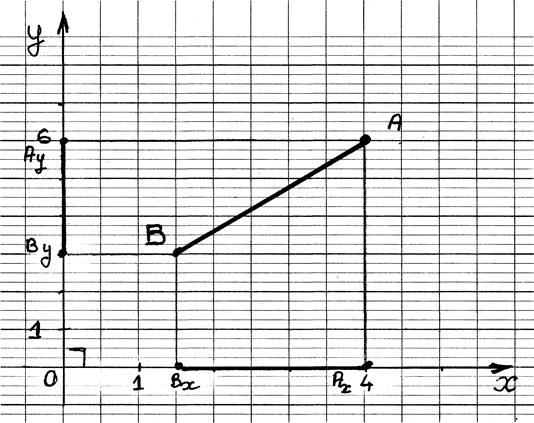
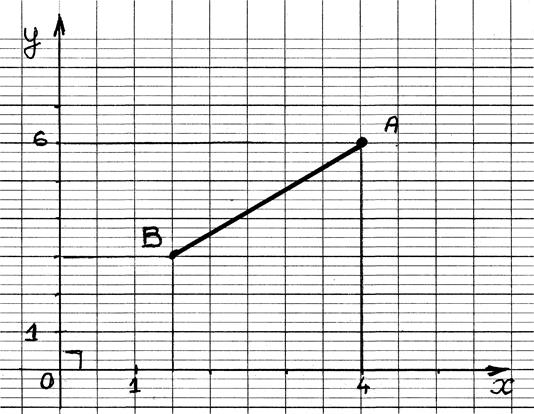
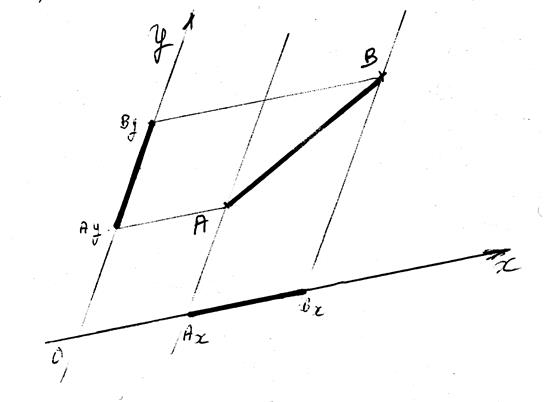
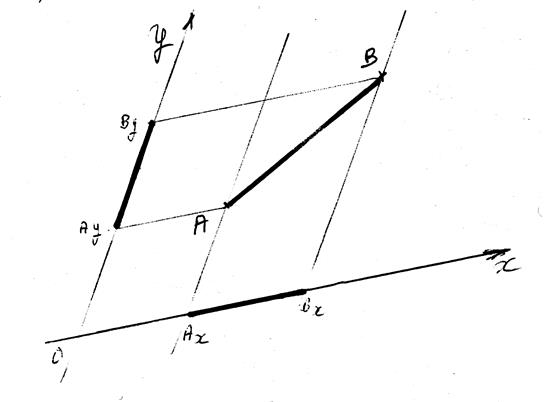
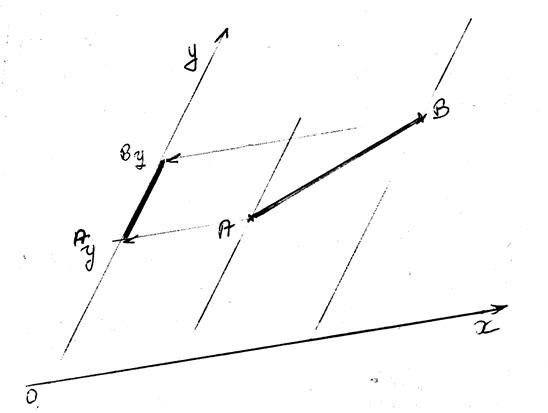
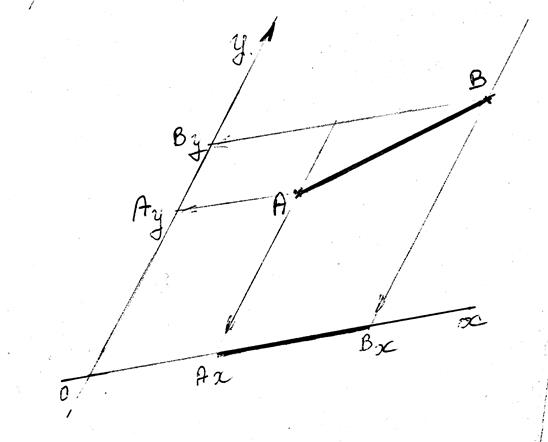
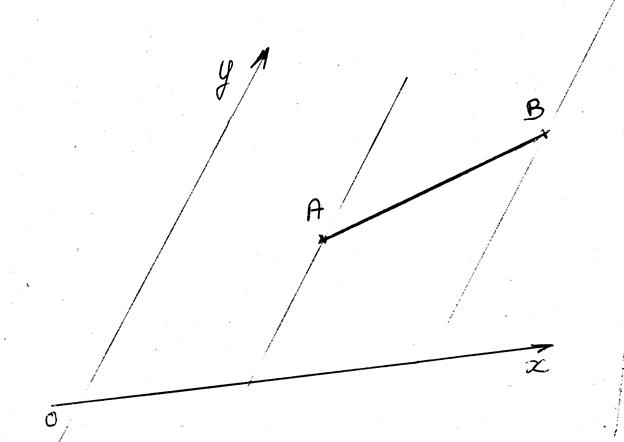
Projections
"ORTHOGONALES" d’un segment
sur deux droites sécantes (appelé aussi repère cartésien ) ,cas courant
le repère est dit « cartésien ortho
- normé » voir Objectif :....FL et F affine )
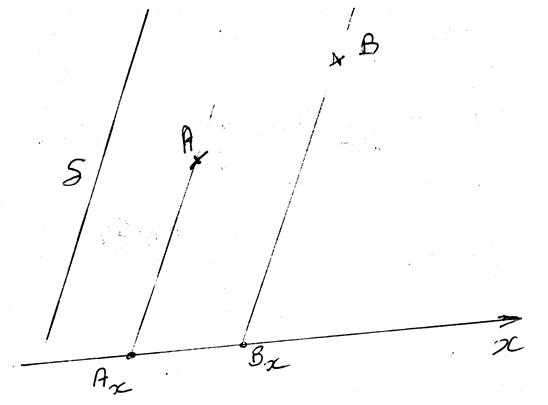
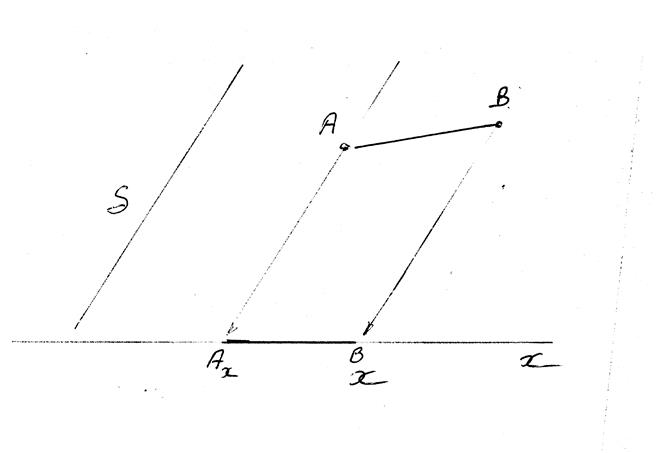
Les
segments de droites Ay By et BxAx sont appelés les projetés du segment
AB .
La norme permet de graduer les axes.
Si la norme * sur x et y est égale « mesure » le repère est
dit « normé »
*Voir
[O,I] et [ O, J ]
y
Ay
A
By B
Bx Ax x
TRAVAUX AUTO
FORMATIFS.
EVALUATION :
A
)
Montrer par un dessin ,la
projection orthogonale d’un point .
D1 D
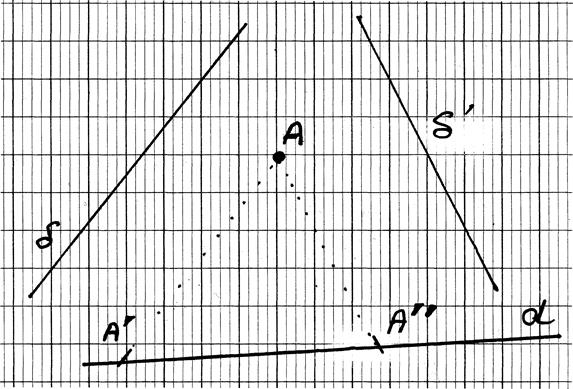
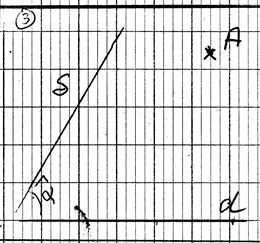
I ) Soit le schéma suivant ,tracez le projeté du point M par
rapport à « delta » sur la
droite D et la droite D1.
M delta
B
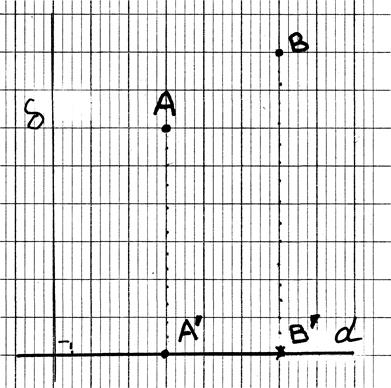
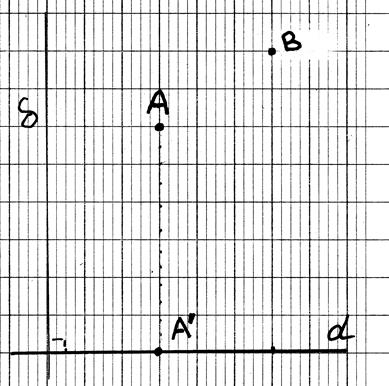
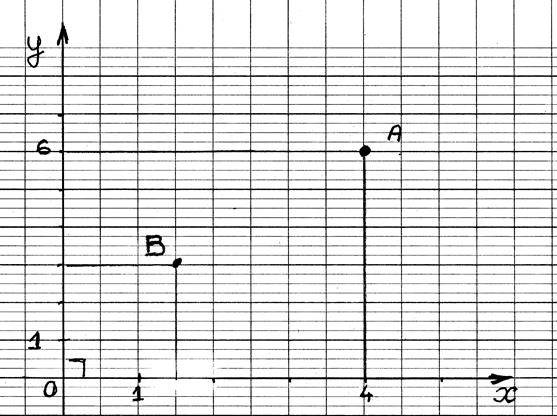
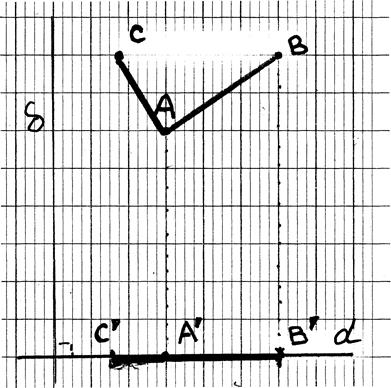
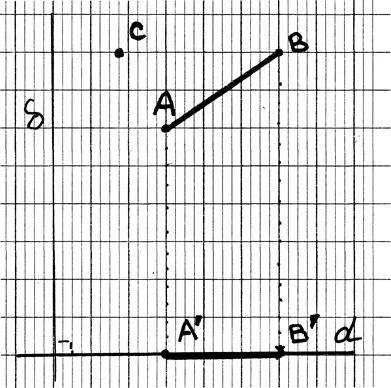
Soit un
repère orthonormé ( à compléter):
tracer les projections du segment
AB ; donner les coordonnées des deux points,
échelle1
Cet exercice sera repris avec Obj : « Pythagore » ; en vue de rechercher la norme
d’un vecteur par le calcul
( Voir la : symétrie orthogonale )
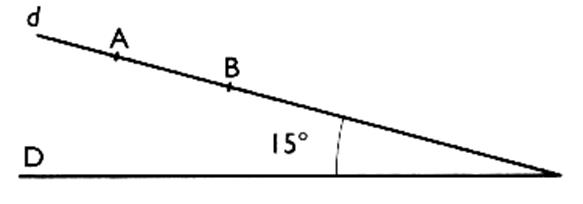
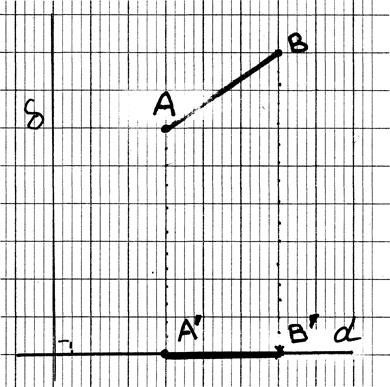
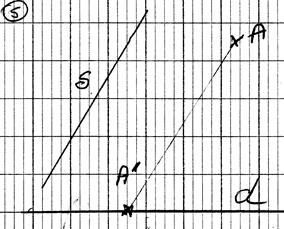
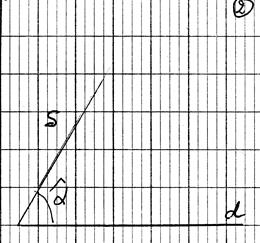
Sur la
droite "d" , les deux points A et B sont distants de 5 cm .
|
Déterminer
la longueur de [ A' ; B '] , projeté
orthogonale sur (D ) de [A B] |
|
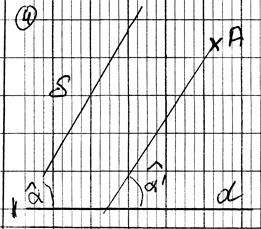
Même
question avec des angles de 30° ; 60 °
et 90°