Index warmaths		Cours sur les vecteurs
	1°) Définition du barycentre
	2°) Construction du barycentre
	3°) Propriété fondamentale du barycentre	SOS cours sur le barycentre..
	4°) Coordonnées du barycentre

Exemple de calcul du Barycentre en sciences
1°) Définition du barycentre
Prenons une plaque triangulaire, posons dessus au point A un poids de 1kg, en B un poids de 2kg, en C un poids de 3 kg, et cherchons le point où l'on pourra faire tenir cette plaque en équilibre. Ce point est appelé le barycentre du système . Notons le G (il n'a rien à voir avec le centre de gravité du triangle). Si on veut déterminer sa position sur la plaque, il faut savoir qu'il est caractérisé par la relation :1. + 2 + 3 = 0 . D'une manière générale, le barycentre G de vérifie toujours . + + = .. Attention tout de même, le barycentre n'existe pas lorsque la somme des coefficients associés aux points est nulle. Par contre l'éventuelle présence de coefficients négatifs ne gène pas. 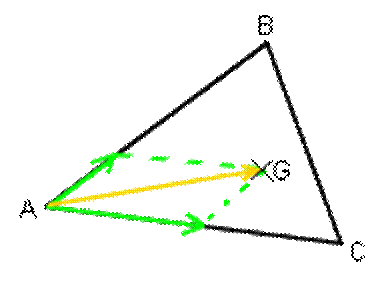2°) Construction du barycentre Pour construire le barycentre sur le dessin, il faut utiliser la propriété ci-dessus et décomposer 2 des 3 vecteurs en fonction de vecteurs que l'on peut tracer. C'est assez simple mais long :
	1. + 2 + 3 = . + 2 (+) + 3 (+ ) = 6 + 2 + 3 = + 2 + 3 = - 6 + 2 + 3 = 6 + = = +	D’où la position de « G »
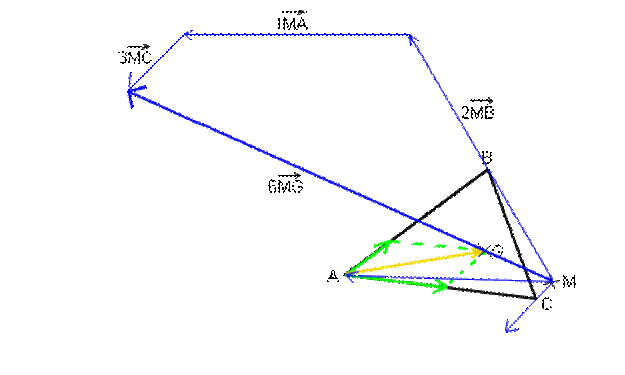
3°) Propriété fondamentale du barycentre Si G est le barycentre du système , alors pour tout point M du plan, on a : . + + = . ( . + + ) Le dessin ci-dessous avec les chiffres du début l'illustre parfaitement. Dans la pratique et dans les problèmes il faut en général placer M à un endroit particulier pour démontrer certaines choses. 4°) Coordonnées du barycentre Si « A, B, et C » sont 3 points dans un repère orthonormé, avec «  A ( xA ; y A) ; B ( x B ; y B) ; C ( xC ; yC) , et que « G » est le barycentre de , alors les formules suivantes donnent les coordonnées de G : Les formules du barycentre se généralisent « bien sur » dans le cas où il y aurait plus de 3 points, on peut également prendre le cas particulier plus simple avec seulement 2 points. Enfin il faut savoir que le barycentre d'un système de points qui ont tous le même coefficient (le même poids) s'appelle l'isobarycentre.

div>