FL : Pré requis
|
Fonction "généralités" |
|
|
Les Grandeurs proportionnelles |
ENVIRONNEMENT du dossier
|
|
DOSSIER LA FONCTION LINEAIRE : Le GRAPHE
d ‘ une fonction .
1°)
On peut obtenir un
tableau de proportionnalité à partir d’ un
graphe
2°)
On peut obtenir un
tableau de proportionnalité à partir d’une équation.
3° ) On
peut obtenir un tableau de
proportionnalité à partir d’une représentation graphique
Attention : ne pas confondre
« graphe d’une fonction et représentation graphique d’une
fonction » ….
|
TEST |
COURS |
Interdisciplinarité |
|
INFO COURS.
Mode de représentation le Graphe de la fonction linéaire
(construit à partir d’une équation)
A )
Application :
Le graphe est un ensemble (ou
suite) de couples de nombres ;du type : {(
x ; ax)
le premier nombre est attribué à « x »
le deuxième nombre est associer à « ![]() x ».
x ».
Si « a » vaut ![]() ,le couple aura la forme et sera noté :(
x ;
,le couple aura la forme et sera noté :(
x ; ![]() x)
x)
B ) Modèle mathématique :
G = {( x1 ;
![]() x1) ; (x2 ;
x1) ; (x2 ; ![]() x2 ) ; ......... }
x2 ) ; ......... }
C ) Construction d’un couple de nombres (à
partir d’une équation) :
Si l’on donne une valeur à
« x » (exemple : 9 )
On obtient un autre
nombre en utilisant l’équation y = ![]() x ; (y =
x ; (y = ![]()
![]() 9 =(18 :3 ) =6)
9 =(18 :3 ) =6)
nous obtenons le premier
couple de nombres du graphe de la fonction « ![]() x » : (9 ; 6)
x » : (9 ; 6)
On remarque que l’on peut citer
un couple particulier : (0 ;0)
D) Conclusion :
le graphe représentant l ’ équation y = ![]() x est G = {(
0 ; 0) ; (9 ; 6 )}
x est G = {(
0 ; 0) ; (9 ; 6 )}
Représentation graphique
I) à
partir d’un graphe :
soit le
graphe obtenu précédemment G = {( 0 ; 0) ;
(9 ; 6 )}
,ces deux couples de nombres permettent de tracer la
représentation graphique de la fonction .
Procédure : reporter les
deux points ; O ( 0 ; 0) ;
A(9 ; 6 )
Remarque : Dans un repère
cartésien , pour le couple (![]() 1 ;
1 ; ![]()
![]() 1)
1)
à x1 on
associe l’abscisse « ![]() »
»
à « ![]() x1 » on associe l’ordonnée «
x1 » on associe l’ordonnée « ![]() 1 »
1 »
Si on analyse ce graphe : G = {( 0 ;
0) ; (9 ; 6 ) }
On reconnaît
que la droite passe par zéro ,on peut
dire le second couple de nombres (9 ; 6 ) est de la forme (x ; ax) ; donc nous avons à faire à un graphe
représentant une fonction linéaire d’équation
y = ax
;le nombre « 9 » est la valeur de « x » ;le
nombre « 6 » est la valeur de « y » ;nous remplaçons
ces valeurs dans l’équation ( y =ax devient 6 = a ![]() 9 , nous en
déduisons que a =
9 , nous en
déduisons que a =![]() , après
simplification a =
, après
simplification a =![]() ;
;
Nous
concluons : le graphe G = {( 0 ;
0) ; (9 ; 6 ) } donne l’équation de la fonction linéaire 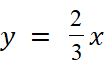
Plus
généralement on dira : que le Graphe de la fonction linéaire est de
la forme :
G = {( 0 ; 0 ) ; ( x1 ;
ax1) ; (x2 ;ax2 ) ; ......... }
Avec
comme les deux couples particuliers :
( 0 ;
0 ) et
( 1 ; a )
TRAVAUX AUTO FORMATIFS.
1°) Donnez la forme des couples qui forment eux mêmes
le graphe de la fonction linéaire.
2°) Donner forment
du graphe de la fonction linéaire. ( donner les deux
couples particuliers)
1°) Soit les fonctions :
|
y1
= 2x |
y2
= - 2x |
y3
= - |
Donner un graphe pour chaque fonction (minimum 3 informations )
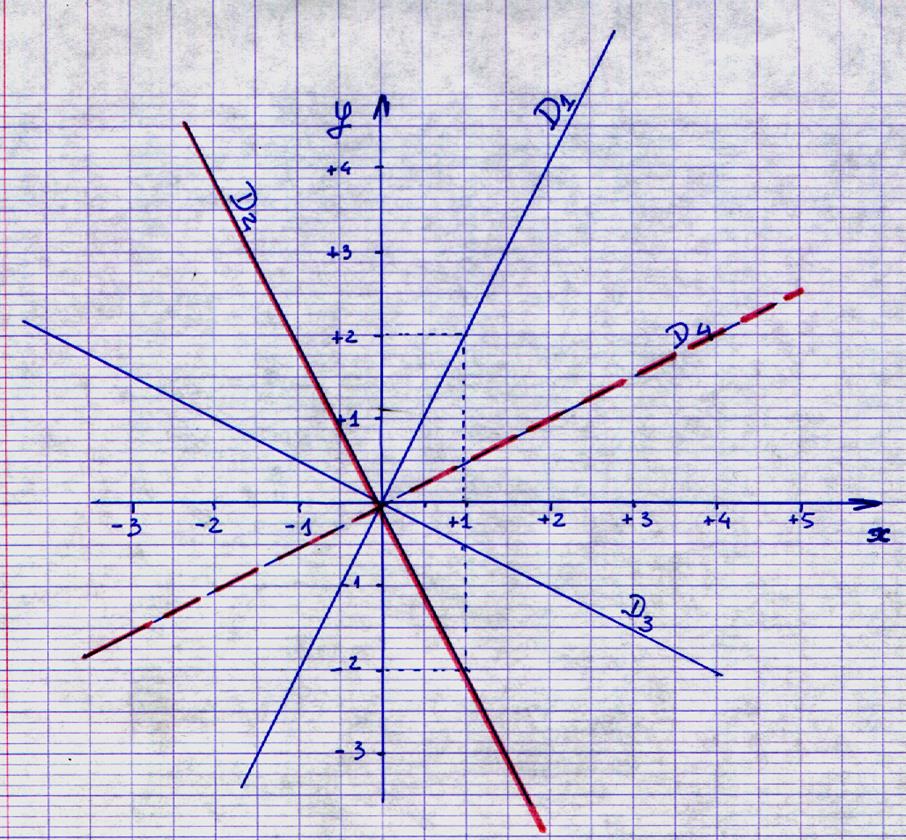
2°) A partir
des représentations graphiques suivantes , donnez un
graphe pour chacune d’elles .
(minimum 3 informations , les indiquer sur les
droites) )