|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
||
|
Série précédente
: Déjà étudiés : exemples |
Série
suivante : Autres exemples de tracés |
||
|
|
|
||
Pré requis - Etude des droites dans un repère.
RÉSOLUTIONS GRAPHIQUES DES PROBLEMES D’ ALGÈBRE
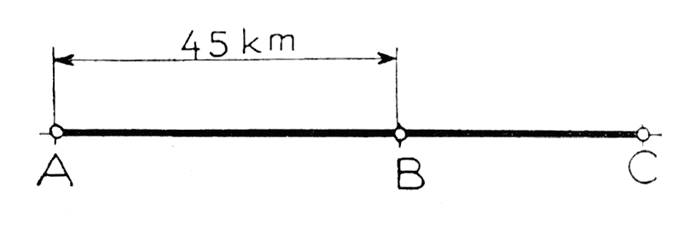
PROBLÈME I. Trois
villes A, B, C, sont placées dans cet ordre sur une route et la distance de A à
B est 45 km. Un cycliste part de A et au même instant un piéton part de B, tous
deux se dirigent vers C. La vitesse du cycliste est 4 fois celle du piéton.
1°) A quelle
distance de B le cycliste rattrapera-t-il le piéton?
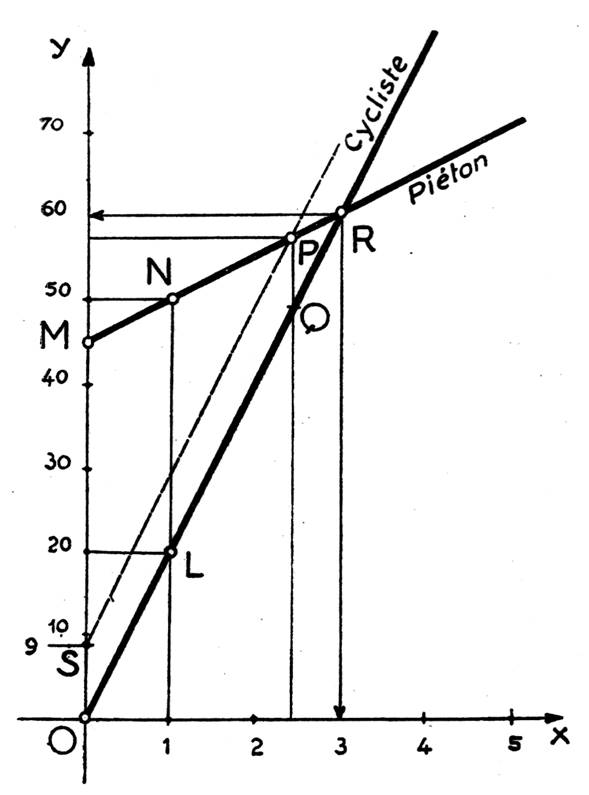
2°) Tracer le graphique des deux mouvements en
portant en abscisses les temps (1 cm pour I heure) et en ordonnées les
distances comptées a partir de A (1 cm pour 10 km).
On supposera que la vitesse du piéton est de 5km/h.
3°) Chercher sur le graphique à quelle distance
de B était le piéton quand son avance sur le cycliste n’était plus que de 9 km.
|
|
|
|
RÉSOLUTIONS GRAPHIQUES DES PROBLEMES D’ALGÈBRE
PROBLÈME II .
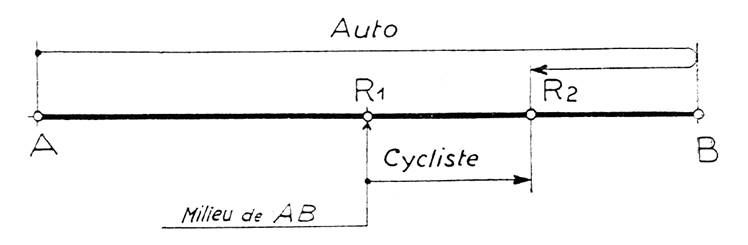
Une
auto fait un voyage aller et retour, sans arrêt, entre deux villes A et B. A
l’aller (sens de A vers B), elle dépasse un cycliste au milieu du parcours AB;
au retour, elle le croise au quart du parcours à partir de B. Les vitesses des
deux mobiles sont constantes.
1°) Si x km représente la distance des deux
points de rencontre, exprimer en fonction de x les distances parcourues par les
mobiles dans l’intervalle des deux rencontres. En déduire le rapport des
vitesses.
2°) La
vitesse du cycliste est 20 km/h. Le temps écoulé entre les deux rencontres est
I h 30 minutes. Calculer la distance AB. Préciser la position du cycliste au
moment du départ de l’auto.
3°) Représenter sur un même graphique la marche
de l’auto et celle du cycliste. Coordonnées des points de rencontre.
Equation
de la droite qui représente la marche du cycliste.
|
|
|
|
PROBLÈME
III.
On
considère un triangle ABC dont les mesures des côtés sont:
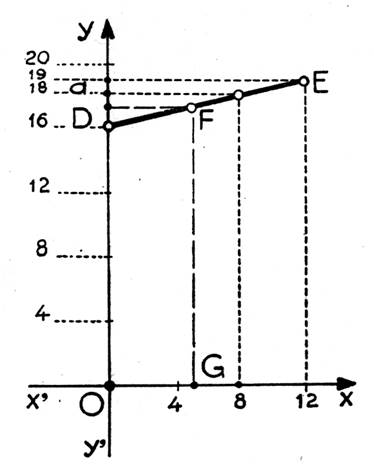
AB = 16 cm, AC = 19 cm, BC 12 cm. Par un
point M du segment BC, on trace la parallèle a AB qui coupe AC en P, puis la
parallèle à AC qui coupe AB en Q.
1°) Evaluer en fonction de BM x, le périmètre 2y
du parallélogramme MPAQ. Variations de y et
représentation graphique.
2°) Déterminer x pour que y ait une valeur donnée
a et discuter:
a) par
le calcul;
b)
graphiquement.
Application
numérique y = 18.
|
|
|
FIN
DES PROBLEMES RESOLUS .
SITUATIONS PROBLEMES (corrigé non fourni )
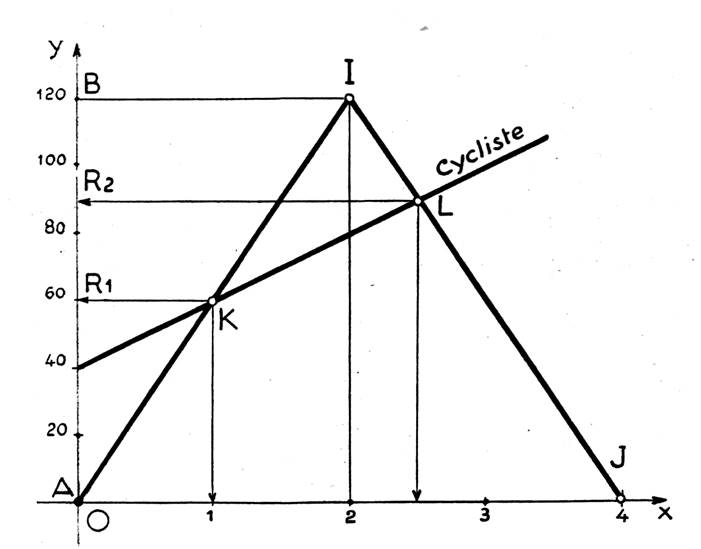
Problème 4 . Deux villes A et
B sont distantes de 120 km. Un motocycliste part de A à 8 h et se dirige vers B
à 40 km à l’heure. Une automobile part de B à 9 h 20 mn et se dirige vers A à
60 km à l’heure.
1°) Représenter graphiquement la
marche des deux mobiles.
2°) Déterminer graphiquement
l’heure et le lieu de la rencontre,
3° ) Solution algébrique. (B.E.P.C. Besançon.)
Exercice 1 .. Première figure.
Tracer
deux axes de coordonnées rectangulaires OX et OY. Placer sur OY le point A
d’ordonnée + 4 et sur OX le point B d’abscisse — 3 (le centimètre est pris pour
unité).
Calculer
AB.
Calculer
l’abscisse du point C de OX tel que le triangle ABC soit isocèle. On trouvera
trois solutions correspondant aux trois cas possibles : AH = AC
BA=BC;
CA=CB.
Exercice 2 .
Deuxième figure.
Tracer
deux axes de coordonnées rectangulaires OX et OY.
Placer
le point A de coordonnées, x = 0, y = 4, le point B de coordonnées x = —3, y = 0, et le polnt
C de coordonnées x = 7 / 6
, y = O (le centimètre est
pris pour unité).
1°) Trouver l’abscisse du point D de
OX tel que le triangle ABD soit rectangle en A.
2° ) Calculer la distance AD et le rapport ( AB / AD ) .
3°) Calculer l’abscisse du point E
de OX tel que
la
mesure algébrique de EB par la mesure algébrique de ED est égale à la fraction
moins 3 sur 4.
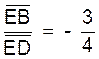
Que dire de la droite AE?
( B.E.P.C. BORDEAUX)
Problème 6 ..
Un
alliage d’or et de cuivre a un volume de 1 cm3 .
La densité de l’or est 19,3 et celle du cuivre 8,8.
1°) évaluer la
masse « g » de l’or contenu dans cet alliage en fonction
de la masse « x » du cuivre,
masses exprimées en grammes. Représenter
graphiquement la variation de la masse de l’or en fonction de la masse du cuivre. Sur les deux axes, 1 g sera
représenté par 1 cm.
2°) Evaluer la masse totale
« z » de l’alliage en fonction
de la masse du cuivre qu’il contient. Représenter graphiquement la variation de
cette masse totale en fonction de la masse de cuivre, sur la même figure que
dans la première question.
3°) Déterminer graphiquement de la
masse de l’or contenu dans l’alliage lorsque la masse totale
est 10 g.
40) Déterminer
graphiquement la masse d’or contenu dans l’alliage lorsqu’il est égal à la
masse du cuivre.
Problème 6. Un voyageur qui se rend à pied de la ville A à la ville B part à midi
en faisant en moyenne 80 m à la minute. A une certaine distance de A, il monte
dans un autobus qui part à midi 22 mn de A pour aller également en B, faisant
en moyenne 40 km à l’heure.
Le
voyageur arrive 1 h 6 mn plus tôt que
s’il avait continué à marcher à pied.
On
demande
1°) A
quelle distance de A il est monté en autobus
2°)
Quelle est la distance de A à B.
3°) Représenter graphiquement le mouvement
du voyageur, du point de départ au point d’arrivée, en prenant en abscisses les
temps (i mm pour une minute) et en ordonnées les espaces (1 cm pour 1.000 m).
Ecrire
l’équation du mouvement correspondant aux deux parties du trajet du voyageur.
4°) Indiquer comment on peut, à
l’aide du graphique, retrouver les résultais des deux
premières questions.
(B.E.P.C. RENNES.)
exercice 3 . On
considère le triangle ABC dont les côtés ont pour longueurs BC = 3 cm, CA = 6
cm, AB = 5 cm. Soit E un point variable du côté AC. La parallèle menée à AB par
E coupe BC en D et la parallèle à BC menée par E coupe AB en F. On pose AE = x.
1°)
Construire le triangle ABC.
Calculer
en fonction de « x » les
longueurs AF, DE et BD.
2°)
Déterminer « x » de façon que AE
= BF.
Si E a
la position ainsi déterminée, que représente AD dans le triangle ABC ? En
déduire une construction géométrique du point E.
3°)
Quand E décrit le segment AC, représenter graphiquement, sur un même graphique,
les variations des fonctions Y = AE, Y = BD, Y = BF.
Déterminer,
à l’aide de ce graphique, comment il faut choisir « x » pour que
a) BF>AE;
b) BD<BF<AE;
c) BF < BD.
(B.E.P.C. TOULOUSE.)
Problème 8. Deux amis habitent, l’un la ville A, l’autre la ville B, distantes de
150 km. Ils se donnent rendez-vous en un point M de la route en ligne droite AB
entre A et B tel que AM = « x »
kilomètres. Ils doivent s’y rendre en automobile.
La
voiture du premier (A) consomme 8 litres d’essence aux 100 km, celle du second
(B) consomme 12 litres aux 100 km.
1°) Exprimer
en fonction de z les quantités y 1 et y 2 d’essence nécessaires à
chacun d’eux pour se rendre en M (y1 et y2 en litres).
2° ) Représenter graphiquement sur un même
système d’axes de coordonnées chacune des deux fonctions y 1 et y 2 • (Unités sur l’axe des
« x », 1 cm pour 15 km sui’ l’axe des « y », 1 cm pour 2
litres).
3° ) Calculer « x » pour que les
quantités d’essence nécessaires à chacun des deux amis soient égales. Vérifier
le résultat sur le graphique.
40) Déterminer « x » pour que la consommation totale d’essence
faite par les deux amis soit égale à 16 litres.
(B.E.P.C. LIBAN.)
Exercice 4
1°) Un
rectangle a pour périmètre 21 m et ses deux dimensions sont proportionnelles
aux nombres 4 et 3. Déterminer ces deux dimensions.
2°) Un
autre rectangle a pour longueur 5 m et largeur 3 m. On augmente la longueur et
la largeur de chaque rectangle de la même longueur « x » . Evaluer, en fonction de « x »
, la différence « y » des aires des deux rectangles obtenus
après cette transformation.
3°) Représenter
graphiquement les variations de « y », quand « x » varie de O à 6 m.
Trouver la valeur de
« x » pour laquelle y = 15 m2.
(B.E.P.C.
GRENOBLE.)
Problème 9 :
1°) ) La distance de Paris
à Lyon est de 512 km. Un train parti de Paris à 8 h 50 mn arrive à Lyon à 17 h
22 mn. Le lendemain, il repart de Lyon à. 6 h 30 mn pour revenir à Paris ; il
effectue son parcours avec la même vitesse que la veille. A quelle heure
arrive-t-il à Paris ? Quelle a été
sa vitesse en km/h ?
2°) Chercher
en quel point du parcours le train passe à la même heure que la veille. Il y
aura lieu de calculer la distance de ce point à Paris, et d’indiquer l’heure à
laquelle le train passe en ce point.
3°) Donner
une solution graphique de la question précédente. A défaut de solution,
vérifier graphiquement le résultat obtenu.
(B.E.P.C. PARIS.)
Exercice 5
. Soit un segment AB = 2a, de milieu O,
et deux demi-droites Ax et By perpendiculaires à
AB et d’un même côté.
On considère deux points variables M
sur Ax et N
sur By.
On pose AM = x , BN = y.
1°) Montrer
que si l’on a x + y = b (b constante), la droite MN passe par
un point fixe de la perpendiculaire OZ à AB.
2°) On
donne sur Ail le point C (AC = a /2 ) et sur la
perpendiculaire en C à AB, le point
fixe P (CP = a). Quelle relation existe-t-il entre z et y quand la droite MN
varie en passant par P ?
3°) Quelle
relation doit lier « x » et « y », pour que les droites OM
et ON soient rectangulaires ? Montrer que, dans
ce cas, la droite MN reste tangente au cercle de diamètre AD.
(B.E.P.C.
LIBAN.)
Problème 10 :
. Un cycliste part en promenade à 8 h
20 et veut être de retour à 12 h. A l’aller sa vitesse est de 36 km/b, et au
retour, elle n’est plus que de 30 km/h.
1°) Calculer
à quelle distance de son point de départ il devra faire demi-tour.
2°) Donner une solution
graphique du problème, en construisant les droites représentant la marche du
cycliste
a) à
l’aller
b) au retour.
3°)Déterminer,
à l’aide du graphique, la distance à laquelle le cycliste se trouvait de son
point de départ à 9 h 30. Expliquer le résultat.
(B.E.P.C. MAROC.)
Problème 11 :
. Un terrain rectangulaire ABCD, de longueur AB 12 m et de largeur AD = 8 m, est divisé en trois
parcelles par deux droites AM et AN, M étant situé sur CD entre G et D, et N
sur BC entre B et C.
On désigne DM par z et BN par y.
1°) Exprimer en fonction de
« x » et « y » les aires des trois parcelles.
2°) Déterminer les valeurs de
« x » et « y » pour lesquelles les aires des trois
parcelles ont la même mesure.
30) A quelle relation doivent
satisfaire « x » et « y » pour que les aires des parcelles
ABN et ADM aient la même valeur ‘?Cette relation
permet d’exprimer « y » en
fonction de « x » .
Représentation graphique (unité 1 cm sur chaque axe).
4°) A quelle relation doivent
satisfaire z et y pour que les aires ABN et ANCM aient la même
valeur ? Représentation graphique
de y en fonction de x en utilisant le graphique
précédent.
Pouvait-on prévoir, d’après les résultats déjà obtenus, la valeur des
coordonnées du point d’intersection ? (B.E.P.C. GRENOBLE.)
Exercice 6
. Soit un trapèze AHCD rectangle en A et B. La grande base BC mesure 10 cm,
la petite base AD 7 cm, la hauteur AH 4 cm.
1°) Calculer DC.
2°) M étant un point quelconque de
la demi-droite AX qui porte AB, on mène par ce point la parallèle MN aux bases
(N est sur la demi-droite DY qui porte DC). On pose AM = x. Calculer en fonction
de x les longueurs y et x des segments
DN et MN ; représenter graphiquement leurs variations quand M se déplace sur Ax. (On pourra utilement mener par D la parallèle DZ à AX).
30) Le triangle DMN peut être
Isocèle s! DN égale MN; pour quelle valeur de x cela se produit-il ?
Vérifier ce résultat sur le graphique.
40) Le triangle DMN peut encore
être Isocèle, mais cette fois avec BN = DM. Calculer alors x
.
Peut-on résoudre géométriquement cette question ?
(B.E.P.C. LYON.)
Exercice 7
. Le périmètre d’un rectangle, mesuré en centimètres, est exprimé par le
nombre 2p. Si l’on augmente sa longueur X de 7 cm, et sa largeur Y de 2 cm, sa
surface augmente de 224 cm².
1°) CaIculer en fonction de « p » la longueur et la
largeur du rectangle.
2°) Entre quelles valeurs p
doit-Il être compris, pour que le problème soit possible ?
3° ) Représenter
sur le même graphique les variations de X et de Y lorsque « p » varie
entre les limites déterminées au chapitre précédent (échelle 1/10).
(Les valeurs de « p » seront portées en abscisses et les
valeurs correspondantes de X ou de Y en ordonnées).
4°) Pour quelle valeurs de p le
rectangle sera-t-il un carré ?
Quelle sera alors la valeur commune de X et de Y ? Que représentent
ces valeurs sur le graphique ? (B.E.P.C. BESANÇON.)
Problème 12 :
, La route qui relie deux villes A et B comporte, de A vers B , une montée puis une descente également inclinées. Un
cycliste dont la vitesse moyenne est en montée 10 km à l’heure, en descente 30
km à l’heure, met 1h 30 mn pour aller de A vers B et 2 h 30 mn pour revenir de
B en A.
1°) Calculer la distance des deux
villes au point le plus élevé de la route.
2°) Représenter graphiquement la
marche du cycliste à l’aller et au retour.
(B.E.P.C.
ANTILLES.)
Problème 13 :
. Un cycliste part à 14 heures d’un village A pour se rendre dans un
village B. Il se déplace avec une vitesse moyenne de 24 km à l’heure. Arrivé en
B, il s’y repose 20 minutes, puis il revient en A avec une vitesse moyenne de
20 km à l’heure. Il est de retour en A À 18 heures.
1°) Calculer la distance AB.
2°) Un automobiliste est parti de A
à 16 heures, sur la même route, avec une vitesse de 60 km à l’
heure. A quelle heure et à quelle distance de A rencontrera-t-il le
cycliste ?
On donnera de cette question une solution graphique que l’on vérifiera
par le calcul.
Problème 14 :
. 1°) Représenter graphiquement les variations des fonctions
y
= 20 x y
= 40 x —80
Echelle de 2 cm par unité pour les abscisses et de i cm par 10 unités
pour les ordonnées.
Déterminer les coordonnées du point de rencontre des deux droites
obtenues.
2°) On suppose que
« x » mesure en heures le
temps compté à partir de 8 heures du matin et « y » la distance en km
comptée à partir d’une ville A pour deux mobiles animés d’un mouvement uniforme
partant de A, le premier à 8 heures, le second à 10 heures du matin et dont les
graphiques de mouvement sont portés par les droites précédentes. Ils s’arrêtent
tous deux au moment de leur rencontre. Quels renseignements le graphique vous
donnera-t-il sur le trajet des deux mobiles ? Quelle est la vitesse de
chacun an km/h ?
3°) A quelle heure doit-on faire
partir de A un troisième mobile animé d’une vitesse de 80 km/h pour qu’il
rejoigne les deux autres au point d’arrivée ? Quelle est la fonction que
représente alors le graphique de son mouvement ?
4°) A quelle distance les trois
mobiles sont-ils les uns des autres 15 minutes avant leur arrivée ? On
déterminera cette distance par le calcul et on vérifiera le résultat sur le
graphique. On constate qu’il y a un rapport simple entre les distances des
trois mobiles ce rapport est-Il le même à tous les moments de la course ?
5° ) Entre
quelles heures pourrait-on faire partir le troisième mobile, toujours avec la
vitesse de 80 km/h ai on voulait qu’il double (dépasse) les deux premiers À
moins de 10 km de leur point de rencontre ?
(E.N. AIX-MARSEILLE.)
Exercice 8 Soit
un demi-cercle de diamètre AB = 2R ; sur le diamètre un point H tel que AH = x ; la
perpendiculaire en H à AB coupe le demi-cercle en M.
1°) Calculer en fonction de
« R » et de « x » :
![]()
Calculer
x de telle sorte que y1
= y2
2°) Représenter sur un même
graphique y1 et y2,
« x » variant de O à
2R.
(On
supposera pour la construction du graphique que R, de longueur 2 cm, est pris
pour unité de longueur).
Utiliser le graphique pour déterminer « x » calculé en 10).
3° ) Soit y3=y1+y2
Calculer « x » de telle
sorte que y3 = kR2 (k: nombre positif donné). Entre quels
nombres doit être compris k pour que le problème soit possible?
4° ) Représenter
graphiquement y3 et retrouver par le graphique les résultats de la
discussion du troisième paragraphe.
(E.N. BESANÇON.)
Exercice 9. Sur l’axe ox d’un système de coordonnées
rectangulaires, on prend un point A d’abscisse + 4 et sur l’axe oy un point B d’ordonnée + 2, puis on joint AB que l’on
prolonge d’une longueur BC égale à AB. Avec AC comme hypoténuse, on construit
dans le demi-plan supérieur un triangle rectangle isocèle ACD.
1°) La construction étant faite,
une simple lecture du graphique donne les coordonnées des points C et D. Indiquer ces coordonnées et vérifier
l’exactitude du résultat en faisant intervenir des considérations géométriques.
2°) Déterminer les équations des
côtés de l’angle droit AD et CD du triangle rectangle ACD.
3° ) On
considère les droites définies par l’équation générale
y = (1/3) x + b.
Entre quelles limites devra-t-on choisir b pour que ces droites coupent
le triangle CAD ?
4°) On suppose que A restant fixe, B se déplace surie demi- axe oy et on appelle ns l’ordonnée variable de B. Exprimer, an fonction de « m », les coordonnées de C et de
D, ainsi que celles du milieu M de AH. Déduire de l’examen des coordonnées de C
et de M les équations et la position des droites sur lesquelles se déplacent
chacun de ces deux points, et donner pour chacune d’elles mie interprétation
géométrique du résultat. (E.N. AIX-MARSEILLE.)
Exercice 10. Le problème porte sur une figure comprenant un trapèze rectangle ABCD
de grande base AB = 3 cm, de petite base CD = 2 cm, et de hauteur AD = 3 cm.
Sur ce trapèze repose un triangle rectangle CDE dont le côté DE placé an
prolongement de AD, a pour longueur 1 cm.
Par un point M, qui décrit le segment AE du point A au point E, on mène
la parallèle à AB qui coupe la ligne brisée BCE an N.
1°) Calculer
MN an fonction de AM = x pour x < 3, puis pour 3 < x < 4.
2° )Dans un système d’axes rectangulaires x ’O
x et y’O y, représenter graphiquement la variation de la fonction y = AM + MN exprimée an
fonction de la variable « x » .
3’) Il peut exister deux valeurs x’ et x ” de x donnant à y la même valeur « m »
quand la longueur « m » est convenablement choisie. Calculer, ou, si
on préfère, déterminer graphiquement
« m » sachant ( x’’ / x’ ) = ( 3
/ 2)
(E.N.
TOULOUSE.)
BON COURAGE - BRAVO si vous faites tous ces exercices et
problèmes !
Warmé Raymond..