Le cercle  et disque

Index warmaths

Objectif précédent :

La sphère (leçon 1 / 3 )

Objectif suivant :

Calcul d’aire et volume d’une sphère et autres formes de parties de sphères….

1.     Liste des cours de géométrie.

2.     Liste des cours sur le volume….

3.     liste des cours de géométrie dans l’espace

DOSSIER : la  SPHERE (leçon :2/3) :  ( niveau 5 :  CAP/BEP)

a)   Définitions :Diamètre ; boule ; développement ;

b)   Génération de la sphère.

c)    Section de la sphère par un plan.

d)   Détermination du diamètre d’une sphère.

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité                         le mouvement diurne

Corrigé Contrôle 

Corrigé évaluation 

COURS

Définition

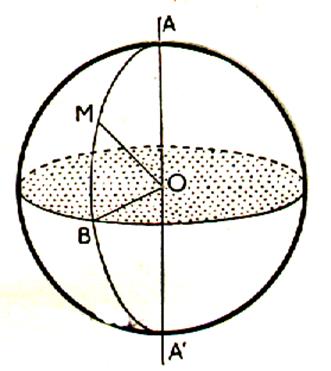
Une sphère est l’ensemble des points M situés à une distance « R » donnée d’un point fixe appelé « centre ».

R = OA = OB = OA’= OM

DIAMETRE :

Une droite passant par le centre de la sphère la coupe en deux points  A et B tels que OA = OB = R . Le segment [AB]  est appelé « diamètre » de la sphère.

Un diamètre d’une sphère est un segment joignant deux points de la sphère et passant par le centre . Tous ces segments ont la même longueur « D » , laquelle est le double du rayon. Cette longueur s’appelle « diamètre » de la sphère .

D = 2R

BOULE :  

 On appelle « boule » de centre « O » , de rayon « R » , l’ensemble des points M tels que OM  £ R ; l’ensemble de ces points représente l’intérieur  de la sphère.

On dit aussi qu’une boule est le solide engendré par un disque effectuant une révolution autour d’un de ses diamètres .

DEVELOPPEMENT D’UNE SPHERE :

Contrairement au cas du cône ou du cylindre , on ne peut pas développer la sphère , c’est  à dire appliquer sur un plan sans pli ou déchirure. Les cartes géographiques ne peuvent donc représenter qu’une partie du globe terrestre , et avec une déformation notable pour une grande étendue ; telle qu’un continent.

GENERATION de la SPHERE :

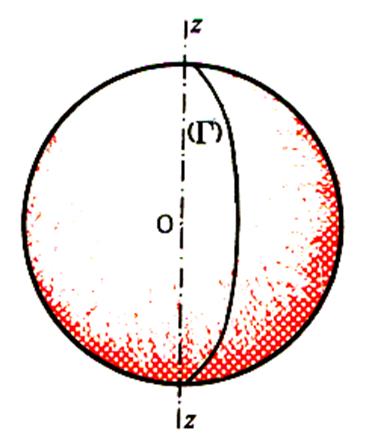
Considérons une droite quelconque ( z’O z) passant par le centre « O » de la sphère et un demi plan de bord ( z’ z ) qui coupe la sphère suivant un  demi – grand cercle.

La  sphère peut être considérée comme engendrée par la rotation de ce demi- grand  cercle autour de l’axe ( z z’) 

Donc :  toute sphère peut être engendrée par la rotation d’un demi – grand cercle autour de son diamètre .

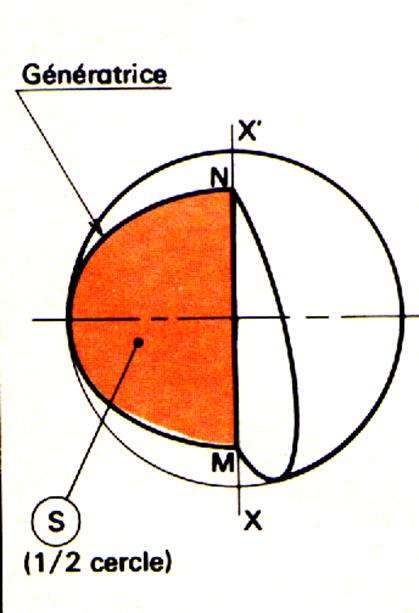
La sphère de révolution 

Une sphère  de révolution est engendrée par un demi-cercle , tournant autour d’un axe xx’ de son plan.

SECTION d’une sphère par un plan.

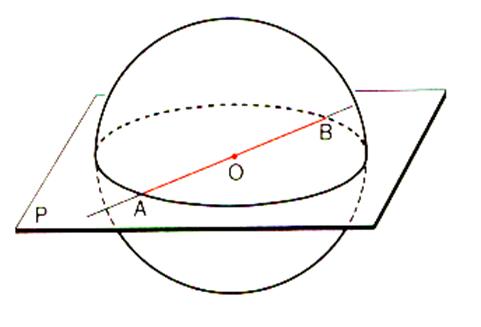
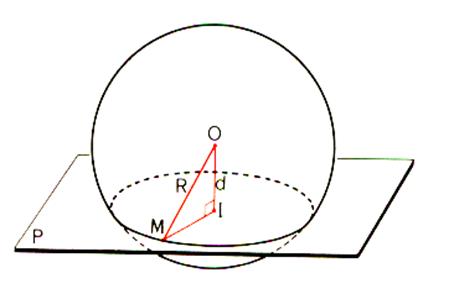
Soit une sphère de centre « O » et de rayon « R » et un plan sécant à la sphère.

Soit OI= d la distance du centre « O » au plan « P ». Soit M un point d’intersection de la sphère et du plan .

On a dans un triangle rectangle OIM :

IM² = OM² – OI² = R²- d²

Donc :

(cliquer ici : pré requis : Pythagore )

Généralisons :

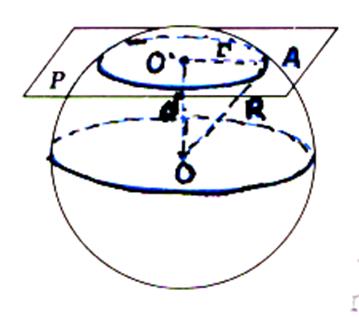
L’ensemble des points communs  de la sphère et du plan est donc le cercle de centre O’ et de rayon  r

    , situé dans le plan P ;

On vérifie bien que ce cercle n’existe que si d £  R . 

Et encore ! ! ! ! !

Si   d = R  , on dit que le plan est tangent à la sphère .

Si d > R , le plan ne rencontre pas la sphère .

Si d < R  , la section est un cercle

Le rayon « r » est inférieur à R , avec égalité si et seulement si d = 0 . C’est pourquoi les sections par les plans passant par le centre ( ou plans diamétraux) sont appelées « grands cercles » de la sphère.

Nota : si on assimile la surface de la terre à une sphère , les méridiens et l’équateur sont des grands cercles

Détermination du rayon d’une sphère :

Le rayon d’une sphère peut   être  déterminé de trois façons : avec le pied à coulisse ; avec le compas d’épaisseur et avec le sphéromètre . 

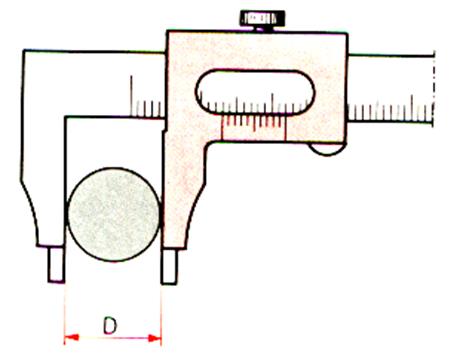
a)avec le pied à coulisse :

Les becs ( mâchoires) du pied à coulisse constituent deux plans tangents parallèles dont la distance est le diamètre de la sphère .

b)Avec le compas d’épaisseur.

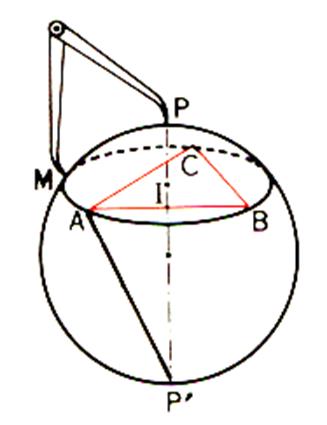
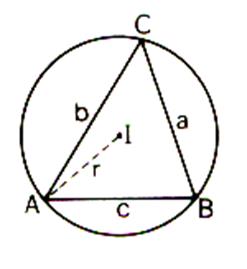
On trace sur la sphère avec « P » comme centre  tel que PM = l   . On marque sur le cercle trois points  A ; B ; C  et on détermine  avec le compas les cotés  AB = c ; BC = a ; CA = b de ce triangle.

on détermine  avec le compas les cotés  AB = c ; BC = a ; CA = b de ce triangle. On peut dans un plan tracer ce triangle  et le cercle circonscrit à ce triangle ,    de rayon r = AI , égal à celui du tracé sur la sphère.

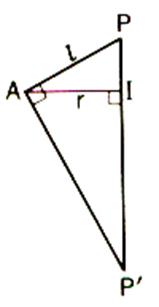
On peut alors tracer le triangle rectangle APP’ dont on connaît la hauteur AI = r  et le côté de l’angle droit AP = l       . On connaît donc le diamètre PP’ de la sphère .

c)Avec le sphéromètre :

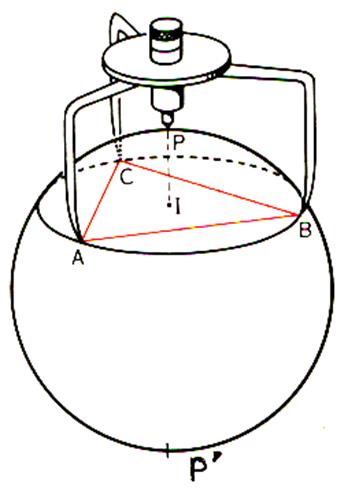
Le sphéromètre est un appareil comportant trois tiges dont les extrémités  A ; B ; C  sont les sommets d’un triangle équilatéral et une vise micrométrique dont l’axe perpendiculaire au plan  ( ABC) passe par le centre « I » du cercle  circonscrit au triangle équilatéral .

Pour pouvoir appliquer les points A ; B ; C  sur une sphère , il faut déplacer l’extrémité « P » de la vis vers le haut d’une longueur  IP que l’on mesure sur un tambour .

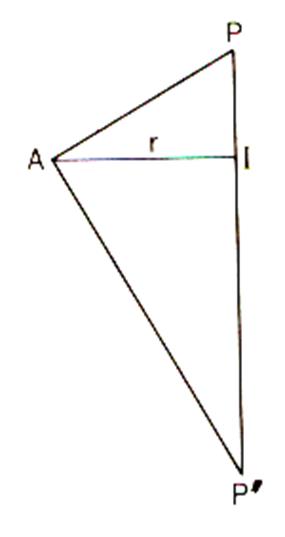
Connaissant le côté [AB] , donc le rayon r = AI du cercle circonscrit et la longueur  PI , on peut construire comme précédemment le triangle rectangle APP’

On peut déterminer la longueur du diamètre du segment [PP’]

TRAVAUX AUTO FORMATIFS.

CONTROLE :

1° ) Donner une définition de la sphère.

2 ° )Donner la définition du rayon d’une sphère

3° )Donner la forme d’une section d’une sphère :

4° ) Qu’est ce qu’une sphère de révolution ?

EVALUATION

Représenter une sphère  ; y représenter le rayon ; le diamètre ; un grand disque (section)