|
Module : les nombres entiers |
DOSSIER : 28 - 29 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
LOGICIEL warmaths ; Pour Aide et
Formation Individualisée
; REMEDIATION mise à /NIVEAU : niveau VI |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
TRAVAUX SOMMATIFS
niveau 6 et 5 Matière : CALCULS
et PROBLEMES |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
LA SOUSTRACTION
avec deux nombres entiers . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
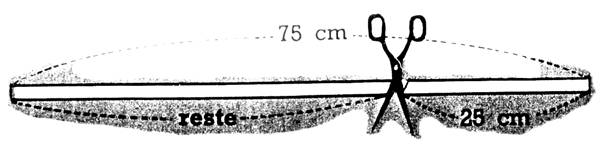
Le sens de l’opération : Explication
n° 1 : mon ruban
mesure « 75 cm » :
Je coupe ; je retranche ; je
retire « 25 cm d’un ruban de 75
cm » La soustraction
est « 75 - 25 » me dit : ce qui me reste
est « 50 cm » |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
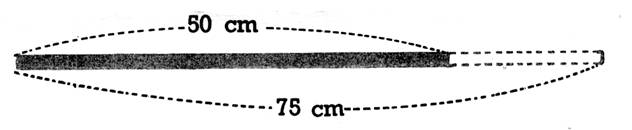
Explication
n°2 :
Combien
manque - t-
il à
50 cm pour que j’aie 75
cm ? Réponse :
la soustraction « 75 - 50 »
me dit ce qui me manque :
« 25» ; l’unité étant des « cm » ; il me manque « 25 cm ». |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Explication
n°3 :
« 75
cm » est plus long que « 50
cm » , (c’est la règle graduée qui permet de le
mesurer) donc :
« 50cm » est plus court que « 75 cm ». ; de
combien ? on
fera la soustraction « 75 -
50 » , le résultat de ce calcul me donne la
différence « 25 » ; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
TRAVAUX CONTROLE |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Les questions relatives à
« ce qu’il faut retenir » , au « savoir » se reporter aux cours . @ info cours
« la soustraction avec les nombres entiers. » |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Que peut-on calculer par une soustraction ? Trouvez la question qui convient, écrivez-la, et posez l’opération 1. Mon livre de lecture a 252
pages; j’en ai déjà lu 138... 2. Catherine possède 395 € ; elle désire acheter un lecture
DVD de 428 € - 3. Une machine à laver coûte 852 €
dans un magasin; la même machine coûte 910 € dans un autre magasin... 4. La charge d’une camionnette est 2 350 kg, celle d’une
fourgonnette 1 880 kg. 5. Pour payer un achat de 769 € , j’ai
donné 800 € 6. Un employé gagne 852 € par
mois; sa femme dépense 684 € 7. Pour la maladie de Pierre , sa maman a
dépensé 112 € - La Sécurité Sociale
lui a remboursé 84 € |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
La
pratique de la soustraction : |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
« exemple : 7 326 - 854 = ? » a)
colonne des unités : On sait que
4 ôté de 6 → reste 2 b)
colonne des dizaines : 2 - 5 →
impossible ; je dis « 5 » ôté de « 12 » → reste « 7 » ,
et je retiens « 1 » centaine. c)
Colonne de centaines :
« 1 » de retenue et « 8 » → « 9 » , ôté de « 3 » →
impossible ; je dis
« 9 » ôté de « 13 » , il reste « 4 » ,
et je retiens « 1 » mille ; d)
Colonne des mille : « 1 » de retenue ôté de « 7 » ,
reste « 6 ». |
7 326 -
854 6 472 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
8. Effectuez : 3639—2587= ………..
; 8632— 4597 = ………… ;
6 508 — 4963 = ………. ;. 9. Retirez 5295 € de 6000 € ; de 10000 € ; de
5500 € 10.
Cherchez les nombres dont
on peut retirer 4 568 et faites les soustractions. (barrer les nombres) 3979; 6729;
9347; 2975; 25638;
10503. 11. Quelle
est la différence entre les nombres suivants : 712 et
584 ? 475 et
719 ? 814 et
586 ?
809 et 645 ? 12. Que
faut-il ajouter à 5 264 pour avoir : 7 845 ? 9 862 ? 7 026 ? 8709 ? 13.
Calculez le grand nombre
des soustractions suivantes :
14. Complétez
les soustractions suivantes
15. Comptez
les soustractions suivantes, puis vérifiez-les par des additions 742—317
; 625—372 ; 646—384 ; 520—286. 16. Comptez,
puis vérifiez chaque soustraction par une autre soustraction 315—184
; 732—566;
430—276; 814—148. 17. J’ai
donné 500 € pour payer un achat de 382
€ ; on m’a rendu 118 €
. Vérifiez que mon compte est exact . a) par une addition; b) par une
soustraction. 18. Dans une course cycliste, 628 km sont à
parcourir en 3 étapes : la 1re , de 238
km; la 2ème , de 196 km. Quelle est la longueur de la 3ème ? 19. Irène et Simone travaillent dans le même atelier
et touchent le même salaire mensuel:425 € .
Irène a dépensé 184 € de son gain, et Simone a dépensé 82 € de
plus que Irène. Combien reste-t-il à chacune? |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
la
longueur des segments représente la même somme « 425 € » |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
20. Hélène
possède 486 € , elle se rend à une brocante pour acheter des appareils
anciens . a) Combien lui restera-t-il si
elle achète le poste de radio ? b) Combien
lui manque-t-il pour acheter l’électrophone? (le
poste de radio = 364 € ; l’électrophone = 542 €) 21. Pour
effectuer un trajet de 612 km, un automobiliste a parcouru 286 km le matin
et 326 km l’après-midi. Écrivez le
titre des opérations suivantes, et indiquez leur résultat: 326 km +
286 km=..............km; 612
km — 326 km=…………………....km ;612 km —286
km=................km. 22. Luc possède 472 € . Il
calcule que, pour acheter un vélomoteur de 668 € il lui manque 204 € . De combien s
‘est-il trompé ? Peut-on le trouver de deux manières? Comment ? 23. Avec
ses économies (245 € ), Julien achète une bicyclette
de 228 € . Combien lui manque-t-il pour la munir d’une paire de sacoches de
86 € ? |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||