Module : Géométrie.		DOSSIER : 156 – 157 _ EXO_
warmaths ; Pour Aide et Formation Individualisée ; REMEDIATION mise à /NIVEAU : niveau VI
Info conseils et consignes.	TRAVAUX NORMATIFS PRIMAIRE / COLLEGE : / Reprise lycée. Matière : MATHEMATIQUES. Niveau VI - V - IV		.
VOLUME DU PARALLELEPIPEDE rectangle et du CUBE.
INFO COURS :
Info 1 @ « cours sur dos. 152 - 153… » ; Info 2 @ « cours sur 146 - 147… » ; Info 3 @ « cours niveau V »

1. Copiez et complétez le tableau suivant, concernant des parallélépipèdes rectangles:
longueur	12 cm		0,9 m		8 cm		8 m		12 m
largeur	8 cm		0,75 m		45 mm		7,5 m		2,5 m
hauteur	10 cm		60 cm		32 mm		3,5 m		5 cm
surface de base	96 cm².		…0,675 m².		…36 cm²….		…60 m² .		…30 m²….
volume	960 cm^3		0,405 m^3		115,2 cm^3		210 m^3.		1,5 m^3
2. Copiez et complétez le tableau suivant, concernant des cubes
Arête		4 cm		10 cm		1,2 m		0,25 m		0,40 m
Surface d’une face		16 cm²		100 cm²		1,44 m²		0,0625 m²		0,16 m²
Surface totale		96 cm²		600 cm²		8,64 m²		0,375 m²		0,96 m².
volume		64 cm^3		1 000 cm^3		1,728 m^3.		0,015625 m^3.		0,064 m^3.
3. Une citerne cubique mesure 1,5 m d’arête. Indiquez le calcul de son volume : a) en m^3 = 1,5 m x 1,5 m x 1,5 m = 3,375 m^3 b) en dm^3. = 15 dm x 15 dm x 15 dm = 3 375 d m^3 Quelle règle des mesures de volume retrouvez-vous dans les résultats ? la règle des 1000 en 1000 4. Une boîte parallélépipédique mesure 24 cm de long, 18 cm de large, 16 cm de haut. a) Évaluez ses dimensions en dm, puis en m. en dm : mesure 2,4 dm de long, 1,8 dm de large, 1,6 dm de haut. En m : mesure 0,24 cm de long, 0,18 m de large, 0,16 m de haut. b) Calculez son volume : en cm^3, en dm^3, en m^3. 0,24 m x 0,18 m x 0,16 m = 0,006912 cm^3 2,4 dm x 1,8 dm x 1,6 dm = 6,912 cm^3 24 cm x 18 cm x 16 cm = 6912 cm^3 c) Citez la règle des mesures de volume que vous vérifiez ainsi. 5. On creuse une fosse de 2,4 m de long, 1,8 m de large, 1,5 m de profondeur. Le terrassier qui la creuse reçoit 24 € par m^3enlevé. Combien reçoit-il ? volume de terre transporté : 2,4 m x 1,8 m x 1,5 m = 6,48 m cube cout du transport : 6,48 fois 24 = 1 55,52 € 6. A 47,50 € la tonne, combien coûte un bloc de pierre cubique de 0,8 m d’arête, le décimètre cube de pierre pesant 2,6 kg? 63.232 € 7. Combien le volume d’un cube de 16 cm d’arête vaut-il de fois le volume d’un cube de 8 cm d’arête ? Donnez la réponse a) par le calcul; b) par le raisonnement, en vous aidant d’un croquis . 8. Un pilier est formé de cinq pierres cubiques superposées ayant chacune 0,65 m d’arête. Calculez : a) la hauteur du pilier; b) son volume en mètres cubes; c) sa masse le décimètre cube de pierre pesant 2,600 kg. 9. Dites le volume d’un livre de 20 cm de long, 10 cm de large, 3 cm d’épaisseur; d’une chambre de 5 m sur 4 ni, et 3 m de haut; d’une valise de 1 ni sur 0,6 ni, et 0,25 ni d’épaisseur; d’une boîte de 20 cm sur 16 cm, et 10 cm de profondeur; d’un mur épais de 0,5 ni, long de 16 m et haut de 3 m. 10. Une salle de classe mesure 7 ni de long, 6,5 m de large et 4 m de haut. Combien d’élèves peuvent y séjourner avec leur maître, chaque personne devant disposer de 5 m ^3d’air ? 11. Un terrassier creuse une fosse cubique de 1,5 m d’arête. La terre remuée augmente de un cinquième de son volume primitif, 3,375 m^3 + 0, 675 m^3 a) Quel volume a-t-elle après son extraction? 4.05 m^3 b) Pour emporter la terre enlevée, le terrassier utilise une brouette contenant 45 dm^3. Combien emplira-t-il de fois sa brouette? 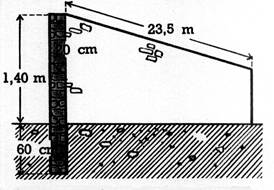4050 / 45 = 90 broutées 12. Un mur, enfoncé de 60 cm dans le sol, s’élève de 1,40 ni au-dessus du sol. Sa longueur est 23,5 m, son épaisseur 20 cm. a) Quel est le volume de la maçonnerie ? b) Le mur a coûté 1546,30 € . Quelle question pouvez-vous poser ? Posez-la, répondez-y.
13. La caisse d’un camion mesure 3,5 m de long, 2 m de large, 80 cm de hauteur. Elle contient une hauteur de 60 cm de sable qui pèse 2,7 t par mètre cube, a) Quel est le volume de la caisse ? 3,5 x 2 x 0,8 = 5,6 m^3 b) Quel est le volume du sable transporté? 3,5 x 2 x 0,60 = 4,2 m^3 c) Quel est le poids de ce sable ? 4,2 x 2,7 = 11 ,34 t d) Vous n’avez pas utilisé le nombre qui mesure le volume de la caisse quelle question pouvez-vous poser ? Faites-le, répondez-y. Quel est le volume non occupé ? 5,6 m^3 - 4,2 m^3 = 1 ,4 m^3 14. Un tas de fumier parallélépipédique mesure 6 m de long, 4 m de large et 1,6 m de haut. Le cultivateur le transporte dans un chariot de 2,4 m^3 et le répand sur un champ à raison de 0,5 m ^3 pour 2 ares de terrain, a) Combien fait-il de voyages aller et retour ? b) Quelle surface peut-il couvrir ?