Module Résumé exo @  :		DOSSIER : 122 - 123
MODULE «  AIRES - SURFACES »
Info conseils et consignes.	COLLEGE / LYCEE Matière : MATHEMATIQUES. ( niv VI)			.
LES SURFACES DECOMPOSEES
INFO COURS :
Revoir les dossiers :102 - 103 ; Info @ cours : les surfaces décomposables
TRAVAUX CONTROLE
Doc WR
Les questions relatives à « ce qu’il faut retenir » , au « savoir » se reporter aux cours .
TRAVAUX : EVALUATION
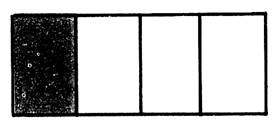
1 - Les figures ci-dessous représentent des surfaces partagées en parties égales; examinez-les, puis calculez de deux façons la surface des parties coloriées.
I ) . Rectangles de 12 cm sur 20 cm			« A »
« B »			« C »
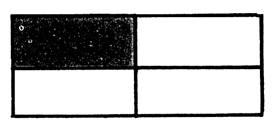
II ) Carrés de 14 cm de côté			« A »
« C »			« B »
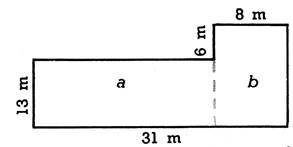
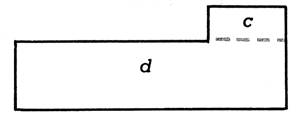
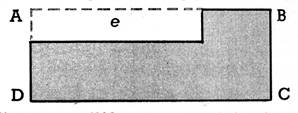
3. Examinez bien le croquis de terrain ci-contre, puis calculez la surface totale de ce terrain . 1° ) en ajoutant les surfaces « a » et « b » ; 2°) en ajoutant les surfaces « c » et « d »; 3°) en retranchant la surface du rectangle « e » de celle du rectangle « enveloppant » ABCD.			1°)
2°)			3°)
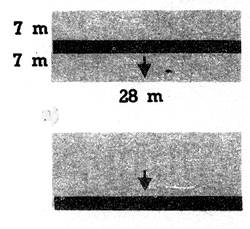
4. Sur une feuille de papier rectangulaire, faites glisser, parallèlement aux côtés, deux bandes coupées à la longueur de ces côtés
On fait glisser en translation la bande noire. De gauche à droite.
On fait glisser en translation la bande noire. De bas vers le haut..
a) La surface d’une bande change -t -elle pendant qu’on la déplace? b) Mesurez les parties découvertes de la feuille, calculez leur surface; la surface totale découverte change-t-elle quand on déplace la bande ?
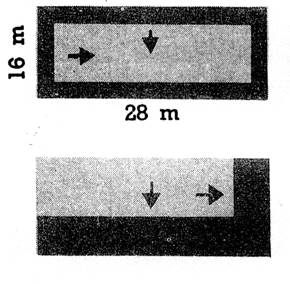
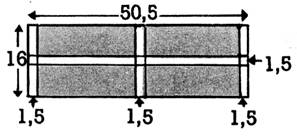
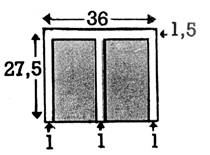
5 Sur les plans de jardins ci-dessous, les allées ont toutes 2 m de largeur. On les déplace pour la commodité des calculs, mais elles gardent leurs dimensions
. Vérifiez, en calculant les surfaces cultivables et leur différence avec la surface totale du jardin, que la surface totale des allées n’a pas varié malgré le déplacement.
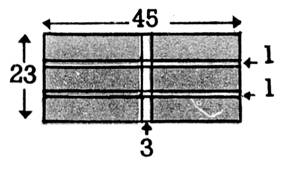
6 - . Reproduire chacun des croquis ci-contre et ci - dessous en double . a) tel qu’il est; b) avec les allées déplacées le long de deux côtés. Calculez alors la surface de la partie cultivable, puis la surface des allées. Nota : Toutes les cotes sont exprimées en mètres
7 . On veut partager un jardin de 32 m sur 25 m en 4 parties cultivables égales, séparées par des allées de 1 m de large, tout en laissant autour de ce jardin une allée de 1,5 m de large, selon une des dispositions ci-dessous. Cherchez la solution qui laisse la plus grande surface cultivable, et dites quelle est cette surface.			« A »
« B »			« C »
8 . Autour d’un bassin carré de 6,5 m de côté, on construit un trottoir de 2 m de large dessinez-le, calculez sa surface.
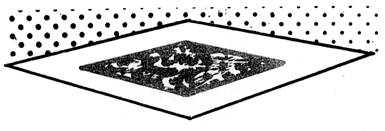
9 . Au centre d’une pièce rectangulaire de 4,25 m sur 3,75 m, on pose un tapis carré de 2,25 m de côté. Quelle surface libre reste-t-il autour du tapis?
10 . Le jardin public représenté ci-contre est un carré de 56 m de côté. Les allées ont toutes 4 m de largeur. a) Quelle est la surface de chacun des quatre massifs carrés ? b) Combien le jardinier mettra-t-il d’heures pour désherber les allées s’il en nettoie 5 m² par heure ?
11 . On veux coller un grand dessin rectangulaire de 0,80 m de large et 1,20 m de long, sur une feuille de carton rigide, qui déborde de 10 cm tout autour du dessin. a) Reproduire le croquis, en y portant les mesures nécessaires. b) Quelles doivent être les dimensions du carton? c) Quel est le prix de cette feuille de carton, qui est vendue à 5,50 € le mètre carré ?
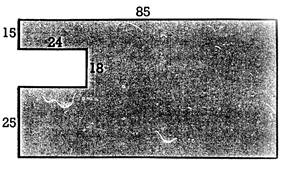
12 J’ai acheté un petit champ dont la forme est donnée par le croquis ci-contre , qui porte, en mètres, les dimensions que j ‘ai pu mesurer. Quelle est, en ares, la surface de mon champ? (Décomposez le champ, pour ce calcul, en surfaces connues). Combien ai-je payé ce champ, qu’on m’a vendu à2 500 € l’hectare?