Module :		DOSSIER : 122 - 123 / EXO
Warmaths  ; Pour Aide et Formation Individualisée ; REMEDIATION mise à /NIVEAU : niveau VI
Info conseils et consignes.	TRAVAUX NORMATIFS PRIMAIRE / COLLEGE/ LYCEE Matière : MATHEMATIQUES. ( niv VI)			.CORRIGE @
LES SURFACES DECOMPOSEES
INFO COURS :
Revoir les dossiers :102 - 103 ; Info @ cours : les surfaces décomposables
TRAVAUX CONTROLE
Doc WR
Les questions relatives à « ce qu’il faut retenir » , au « savoir » se reporter aux cours .
TRAVAUX : EVALUATION
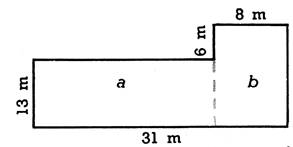
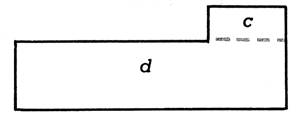
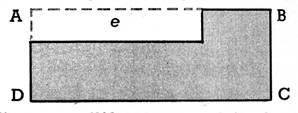
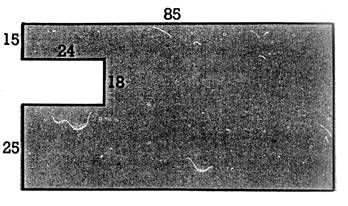
3. Examinez bien le croquis de terrain ci-contre, puis calculez la surface totale de ce terrain . 1° ) en ajoutant les surfaces « a » et « b » ; 2°) en ajoutant les surfaces « c » et « d »; 3°) en retranchant la surface du rectangle « e » de celle du rectangle « enveloppant » ABCD.			1°)
2°)			3°)
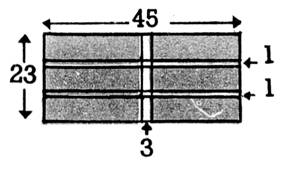
6 - . Reproduire chacun des croquis ci-contre et ci - dessous en double . a) tel qu’il est; b) avec les allées déplacées le long de deux côtés. Calculez alors la surface de la partie cultivable, puis la surface des allées. Nota : Toutes les cotes sont exprimées en mètres
10 . Le jardin public représenté ci-contre est un carré de 56 m de côté. Les allées ont toutes 4 m de largeur. a) Quelle est la surface de chacun des quatre massifs carrés ? b) Combien le jardinier mettra-t-il d’heures pour désherber les allées s’il en nettoie 5 m² par heure ? pour calculer l’aire des allées prendre la méthode par soustraction ou la méthode par addition (numérotez les 9 surfaces )
11 . On veux coller un grand dessin rectangulaire de 0,80 m de large et 1,20 m de long, sur une feuille de carton rigide, qui déborde de 10 cm tout autour du dessin. a) Reproduire le croquis, en y portant les mesures nécessaires. b) Quelles doivent être les dimensions du carton? c) Quel est le prix de cette feuille de carton, qui est vendue à 5,50 € le mètre carré ?
12 J’ai acheté un petit champ dont la forme est donnée par le croquis ci-contre , qui porte, en mètres, les dimensions que j ‘ai pu mesurer. Quelle est, en m² , la surface de mon champ? (Décomposez le champ, pour ce calcul, en surfaces connues). Combien ai-je payé ce champ, qu’on m’a vendu à2 € l’le m² ?