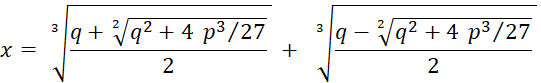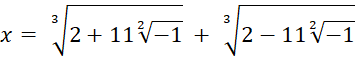Warmaths ( retour index)	MATHEMATIQUES :
		Niveau : supérieur niveau 4
		LES NOMBRES COMPLEXES. Introduction.
	Prérequis : le second degré .
	Nota sur le carré d’un nombre.
	Le « carré » d’un nombre est le produit d’un nombre par lui-même.
	Le carré de « 2 » est « 4 »  ; la racine carrée de « 4 » est « 2 » ; on note :
	Le carré de «   » est «  » ; la racine carré de «   » est «  » ou «   »
	Nota : le carré d’un nombre positif ou négatif est toujours positif .
	Donc « - » ne peut pas être le carré d’un nombre …………. Le carré ne peut pas être un nombre négatif ……….
	Nota sur le cube d’un nombre.
	- Le cube d’un nombre positif est un nombre positif . (calculez : )
	- Le cube d’un nombre négatif est un nombre négatif.
	(calculez : )
Juin 2017
	Naissance de la théorie des nombres complexes.
	Scipione del Ferro (né à Bologne le 6 février 1465 - décédé à Bologne le 5 novembre 1526), est un mathématicien italien, célèbre pour avoir trouvé le premier la méthode de résolution d'équation de troisième degré sans terme quadratique.
	Au XVI^ème siècle un mathématicien nommé : Scipione dal Ferro propose une formule qui donne une solution à l’équation du troisième degré ( 3^ème ) de la forme :
	Vers la fin du XVI^ème siècle un mathématicien du nom de Bombelli applique cette formule à l’équation : , pour la mettre sous la forme : , il obtient littéralement :
	A priori , cette écriture n’a pas de sens puisqu’on ne sait pas ce que représente l’écriture symbolique  noté : , ou écrit plus simplement : .
	Mais Bombelli va plus loin. IL remarque , en utilisant les règles usuelles de calcul que : De ( 1 ) on a et de (2) on obtient : Si bien qu’il obtient : Soit : Or , est bien une solution de l’équation . On peut alors s’interroger : peut-on légitimement calculer avec des symboles imaginaires comme ci-dessus ? C’est ainsi qu’est née la théorie des nombres complexes.
	Les nombres complexes se révèlent très tôt utiles dans la résolution des équations polynomiales, ainsi que l'expose Bombelli dès 1572. Ils permettent également aux mathématiciens de s'intéresser dès 1608 au théorème fondamental de l'algèbre.
	Les nombres complexes prennent naissance au XVIème siècle lorsqu’un italien Gerolamo Cardano (1501 ; 1576), au nom francisé de Jérôme Cardan, introduit −15 pour résoudre des équations du troisième degré. En 1572, un autre italien, Rafaele Bombelli (1526 ; 1573)publie "Algebra, parte maggiore dell’aritmetica, divisa in trelibri" dans lequel il présente des nombres de la forme a + b −1 et poursuit les travaux de Cardan sur la recherche de solutions non réelles pour des équations du troisième degré. A cette époque, on sait manipuler les racines carrées d’entiers négatifs mais on ne les considère pas comme des nombres. Lorsqu’une solution d’équation possède une telle racine, elle est dite imaginaire. La notation i apparaît en 1777 siècle avec Leonhard Euler (1707 ; 1783) qui développe la théorie des nombres complexes sans encore les considérer comme de « vrais » nombres. Il les qualifie de nombres impossibles ou de nombres imaginaires. Au XIXe siècle, Gauss puis Hamilton posent les structures de l’ensemble des nombres complexes. Les nombres sans partie imaginaire sont un cas particulier de ces nouveaux nombres. On les qualifie de « réel » car proche de la vie. Les complexes sont encore considérés comme une création de l’esprit.
	1 – INTRODUCTION.
Info sur les ensembles.	L’équation  : n’a pas de solutions dans l’ensemble , mais elle a une solution dans l’ensemble ( plus grand) :
	Autre exemple : l’équation n’a pas de solution dans ,mais elle a une solution dans l’ensemble ( plus grand que ) noté ensemble : , cette solution est .
	Et l’équation : n’ a pas de solution dans , c’est dans l’ensemble que l’on pourra des solutions.
	Ainsi quand une équation n’a pas de solutions dans un ensemble , la démarche « naturelle » consiste à en chercher dans un ensemble dit « plus grand » .
	On doit maintenant « imaginer » un ensemble plus grand que l’ensemble dans lequel l’équation possédera des solutions . On le notera : , on l’ appellera « ensemble des nombres complexes ». Le principal élément de l’ensemble sera noté ( «  » comme « imaginaire ») Le nombre est tel que D’où l’équation donne ou ; on transforme : ( info : nous avons la forme )
	soit ; donc ou
	2 – CONSTRUCTION DU CORPS DES NOMBRES COMPLEXES.
	A ) Définition : Notons par : l’ensemble des couples de réels : Les éléments de sont appelés des « nombres complexes ».
	Comme il n’est pas pratique de travailler avec des couples ( notations un peu lourdes ) nous allons voir (voir le théorème 1 ci-dessous) que l’on peut noter les éléments de de manière commode et faciliter ainsi le calcul.
	Théorème 1 :
	L’ensemble peut être muni de deux lois et qui prolonge les lois et de . L’ensemble contient « une copie » de L’ensemble . Il existe dans un élément , noté «  » , tel que Tout élément de s’ écrit , de manière unique : , où «  » et «  » sont des réels.		Les règles de calculs ( avec les lois et ) dans seront donc les mêmes que dans en remplaçant ou vice versa.
	Voir la démonstration ci-dessous :
	On muni l’ensemble des deux lois de composition interne suivantes :
	- La première , notée est définie par :
	- La seconde , notée est définie par :
	Par exemple : avec et
	On vérifie facilement que : ( ;  ; ) est un corps commutatif . C’est -à-dire : la loi est associative et commutative , quelle admet un élément neutre et tout élément admet un opposé ;
	Et la loi est associative , commutative , distributive par rapport à la loi , admet un élément neutre et tout élément admet un inverse .