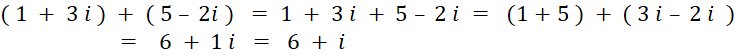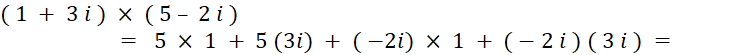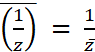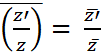Warmaths ( retour index)	MATHEMATIQUES :	Liste des cours niveau bac.
	Niveau : supérieur niveau 4
Retour « sommaire ».	Résumé Classe T S .
	LES NOMBRES COMPLEXES.
	Ensemble et calculs .
Retour …(introduction)…	( les réels et les imaginaires) Et les complexes conjugués.
>>> Complément de formation au résume ci-dessous:
Cours : TERMINALE S . Résumé sur les nombres complexes ( l’ ensemble et calculs types) .
A ) Ensemble des nombres complexes.
Premières définitions :
· L’ensemble des nombres complexes , noté , est l’ensemble des nombres de la forme où et décrivent l’ensemble des réels et où vérifie
· est appelée forme algébrique du nombre complexe. Avec est la partie réelle et la partie imaginaire.
Notation utilisée : si alors et
On peut remarquer : · Un imaginaire pur est un nombre complexe dont la partie réelle est nulle. · Un réel pur est un nombre complexe dont la partie imaginaire est nulle.
B ) Calculs algébriques dans
sont deux nombres complexes tels que
Propriété 1  :
Propriété 2 :
Les règles connues pour l’addition et la multiplication dans s’étendent à
Exemple type : calculez :
			“ i^2= - 1 “
Propriété 3 : Tout complexe admet un unique inverse noté : Conséquence : Comme dans si  ;
Définition : Le complexe conjugué de est le complexe , noté Tel que si z = x + i y , alors
Conjugué et opérations :
Pour tout ,
Si , et
Exercices :
Enoncé : z et z’ sont deux nombres complexes tels que : et
Ecrire les nombres suivants sous forme algébrique :
a) b) c ) d) e )
Autre exercice :
On donne deux nombres complexes : et
Calculer : ;  ;  ;  ;  ;
Travaux auto formatifs
1°) calculez :
Voir corrigé dans le cours…..

2°) Enoncé :

z et z’ sont deux nombres complexes tels que : et

Ecrire les nombres suivants sous forme algébrique :

a) b) c ) d) e )

3°) Autres exercices :

On donne deux nombres complexes : et

Calculer : ;  ;  ;  ;  ;

Corrigé :

Nota : Pour effectuer les transformations et faire les calculs , il faut bien maitriser les cours sur les égalités et les cours sur les opérations avec les nombres relatifs.

2°) on donne : et

Calcul  de

a)

On remplace « z » par le terme ( 2 – 3 i ) et z’ par le terme ( - 1 + i )

A = 2 ( 2 – 3 i) - 3 ( - 1 + i )

A = ( 4 – 6 i ) – ( -3 + 3 i)

A = 4 – 6 i +3 – 3 i

A = 7 – 9 i

b)

On remplace « z » par le terme ( 2 – 3 i ) et z’ par le terme ( - 1 + i )

B = ( 2 – 3 i) ( - 1 + i )

B = 2 fois -1 + 2 fois i + ( -3 i fois -1 ) + ( -3i fois + i )

B = -2 + 2 i + 3 i - 3 i fois i

B = - 2 + 5 i – 3 i² mais : i² = - 1

B = - 2 + 5 i + 3

B = 1 + 5 i

c )

On remplace « z » par le terme ( 2 – 3 i ) ( voir les quantités conjuguées )

C = = = = = = = =

Nota : le conjugué de ( 2 – 3 i ) est ( 2 + 3 i )

Lorsqu’un nombre est complexe est situé au dénominateur on multiplie le numérateur et le dénominateur par son conjugué. ( voir ci-dessus)

D )

On remplace « z » par le terme ( 2 – 3 i ) et z’ par le terme ( - 1 + i )

voir ci-dessus « C »

D =

D =

e ) = ( 2 – 3 i) + = ( 2 – 3 i) +( 2 + 3 i) = 4