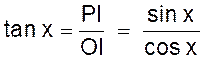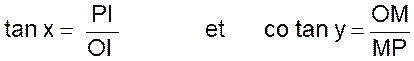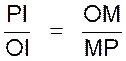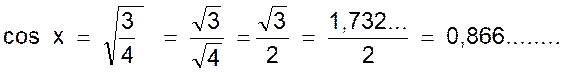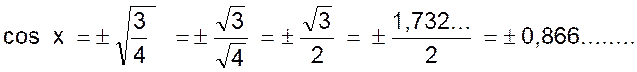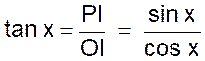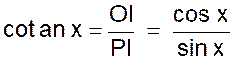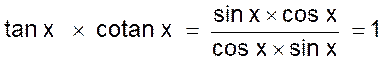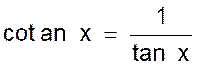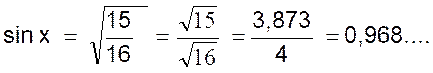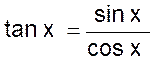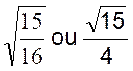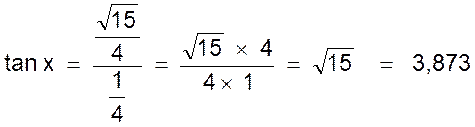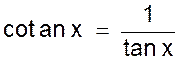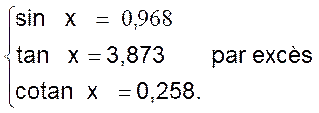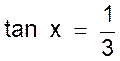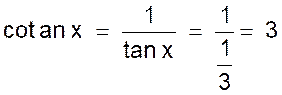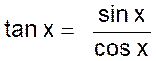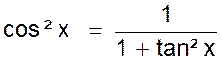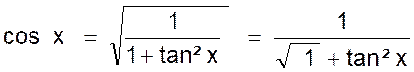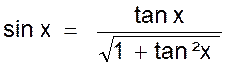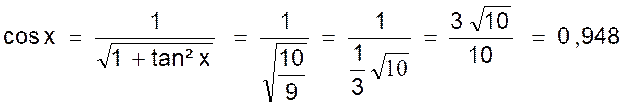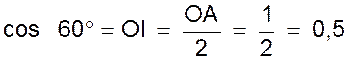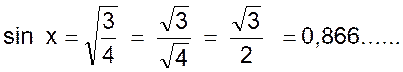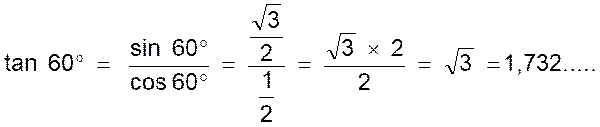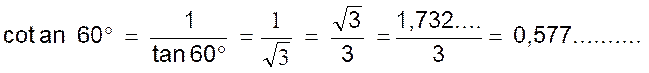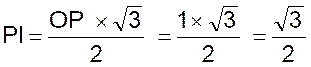Index warmaths		Liste des cours sur la trigonométrie
		Liste des cours sur les fonctions circulaires ; cercle trigonométrique.
Leçon : PROPRIETES DES LIGNES TRIGONOMETRIQUES .
	Chapitres :
	1°) Lignes trigonométriques de deux angles complémentaires.
	2°) Relation entre le sinus et le cosinus d’un angle. : sin ² x + cos ² x = 1
	3°) Relations entre la tangente et la cotangente d’un angle et le sinus et le cosinus d’un même angle .
	4°) Applications :
	Calcul de cosinus x connaissant sinus x ; -calculs des rapports (lignes) trigonométriques  d’ angle connaissant le cosinus et ou connaissant la tangente .

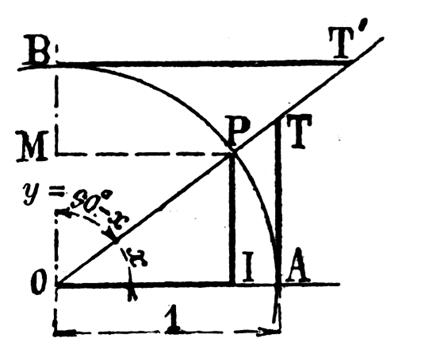
1°) Lignes trigonométriques de deux angles complémentaires.

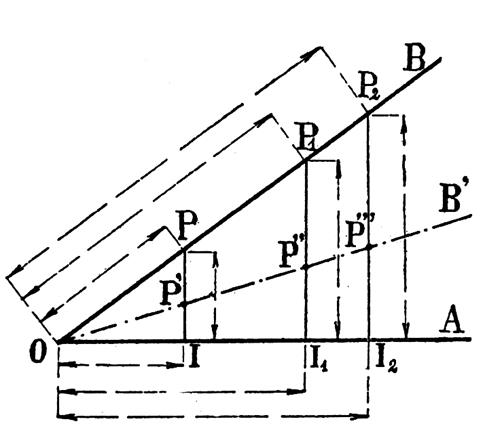
Théorème : Si deux angles sont complémentaires , le sinus et la tangente de l’un sont égaux respectivement au cosinus et à la cotangente de l’autre .

Soit x et y les deux angles complémentaires : y =90° - x puisque l’angle AOB = 90° 1°) on a sin x = PI et cos y = OM ( PM étant perpendiculaire sur OB) . Mais : PI = OM Donc : sin x = cos y Et l’on peut écrire  Sin x = cos ( 90° - x ) ( devient la formule générale)

2°) On a Or : donc tan x = cotan y Et l’on peut écrire la formule générale : tan x = cotan ( 90° - x )

2°) Relations fondamentales entre les lignes trigonométriques :

a) Relation entre le sinus et le cosinus d’un angle. : sin ² x + cos ² x = 1

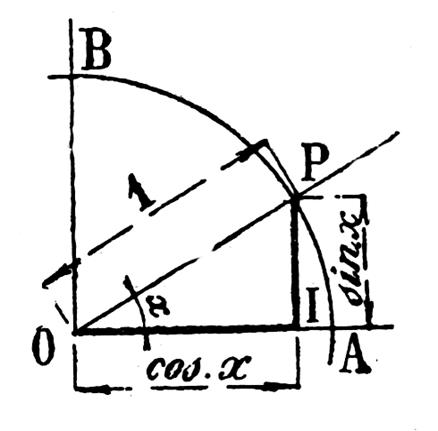
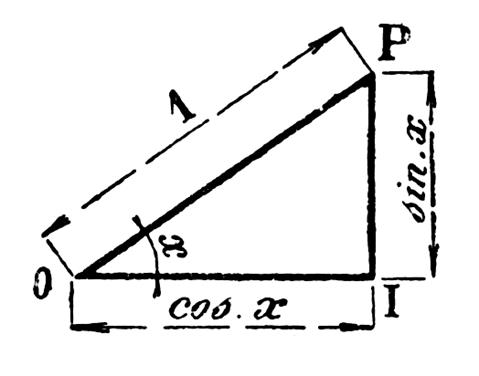
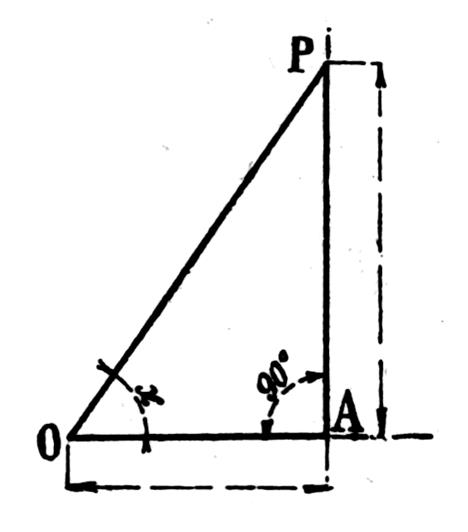
Le triangle rectangle OPI ( ci contre) donne d’après le théorème de Pythagore : et en remplaçant on a : (1) sin ² x + cos ² x = 1 Cette relation importante permet le calcul du sinus d’un angle connaissant son cosinus et inversement de trouver le cosinus si l’on donne le sinus .

Exemple : le sinus d’un angle étant de 0,5 , trouver le cosinus de cet angle .

De sin x = 0,5 , on tire sin² x = (0,5)² = 0,5 fois 0,5 = 0,25 = 1/4 En remplaçant dans la relation (1) on a : 0,25 = cos ² x = 1 d’où cos ² x = 1 - 0,25 = 0,75 ou cos ² x = et remarque : on apprend en algèbre qu’un nombre positif possède deux racines carrées de même valeur absolue mais de signe contraire. On a donc en réalité : nous verrons dans la suite du cours que les deux valeurs de cos x : + 0,866 et -0,866 sont admissibles, la première correspond à un angle aigu x , la deuxième correspond à l’angle obtus supplément de x c’est à dire ( 180° - x )

3°) Relations entre la tangente et la cotangente d’un angle et le sinus et le cosinus d’un même angle .

D ‘ après la définition de la tangente d’un angle on a : (2) et (3) la comparaison des relations (2) et (3) donne immédiatement :

Donc : tan x ´ cotan x = 1

Et

La tangente et la cotangente d’un angle ont donc bien des valeurs inverses l’une de l’ autre . Les relations (1) , (2) et (3) permettent , étant donné la valeur de l’une des lignes trigonométriques d’un angle , de trouver les autres lignes trigonométriques de cet angle.

4°) Applications :

Le cosinus d’un angle étant 1/4 trouver les autres lignes trigonométriques du même angle. 1°) en utilisant la relation (1) , on peut écrire sin² x + cos² x = 1 d’où l’on tire : sin² x = 1 - cos ² x mais si cos x = 1/4 on a cos² x = 1 /16 et par suite : sin² x = 1 - 1/16 = 15 /16 d’où 2°) en utilisant la relation (2) et en remplaçant sin x par et cos x par 1/4 on obtient : Puisque on a : ( on a multiplier en haut et en bas par racine de 15 ) Résultats : Si cos x = 1/4 = 0,25 on a

Exemple 2 : La tangente d’un angle étant donnée , trouver les autre lignes trigonométriques : Exemple numérique : On a immédiatement : La relation (2) donne sin x = tan x ´ cos x Et en remplaçant dans la relation sin² x + cos² x = 1 On aura : ( tan x cos x ) ² + cos ² x = 1 ou tan ²x cos² x + cos ² x = 1 et mettant cos² x en facteur on a : cos² x ( tan² x + 1 ) = 1 d’où et en extrayant la racine carrée avec le signe + , il vient :

En remplaçant cos x par cette valeur dans l’égalité (3) on a : (b) l’application numérique tan x = 1/3 donne et Remarque : les formules précédentes (a) et (b) donnant le sinus et le cosinus d’un angle en fonction de la tangente sont d’un usage assez fréquent dans certaines applications , notamment en électricité ( courant alternatif ) .

Exemple 3 : Calculer les lignes trigonométriques de l’angle de 60°.

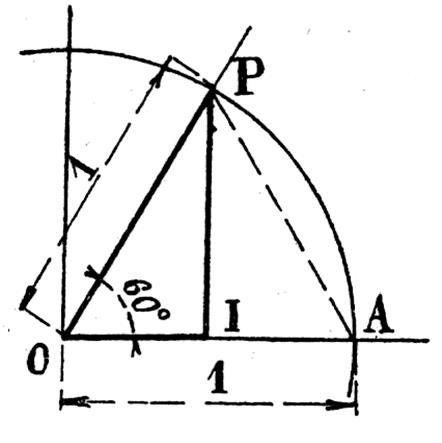
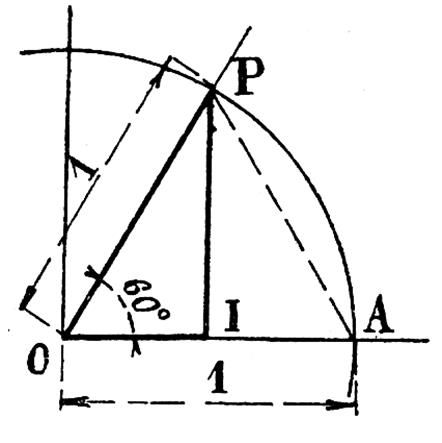
Considérons l’angle de 60 ° ( angle AOP ; Figure ci -contre ) On sait que le triangle rectangle OPI est la moitié d’un triangle équilatéral . On peut donc écrire : 1°) calcul du cosinus :

On est alors ramené au problème (exemple 1) et l’on a successivement : 2°) calcul du sinus : sin² 60° = 1 - cos ² 60° = 1 - (1/2)² = 1 - (1/4) = 3/4 d’où : i

3°) Calcul de la tangente :

4°) Calcul de la cotangente : Remarque : Si l’on se reporte aux propriétés géométriques rappelées en « pré requis) les résultats précédents sont confirmés. On a par exemple PI ou sin 60° = hauteur d’un triangle équilatéral de côté « 1 » , voir ci dessous.

Or PI hauteur d’un triangle équilatéral est égal à :

Cours suivant : lignes trigonométriques des angles 0° ; 30° ; 45° ;60° et 90° .;

CONTROLE :

Citer les formules qui découlent des propriétés et qui mettent en lien les ‘ lignes trigonométriques.

EVALUATION :

1°) Les tables et les calculatrices fournissant les valeurs des lignes trigonométriques donnent « 0 ,415 » pour valeur de sinus « 24° 30’ » . Comparer cette mesure avec celle que donnerait dans un cercle de rayon 100 millimètres , la longueur du sinus du même angle construit avec un rapporteur. ( niv V) 2°) Même exercice avec : tan 55° 30’ = 1,455 (niv VI) 3°) Même exercice avec : cos 37° 20’ = 0,795 (niv IV) 4°) Même exercice avec : cotan. 42° 40’ = 1,085 (Niv V) 5°) Construire l’angle aigu dont le sinus est 0,380. Mesurer l’angle au rapporteur et comparer le résultat avec le nombre de degrés fourni par les tables ou la calculatrice . ( 22°20’) 6°) Construire l’angle dont le cosinus = 0,824 7°) Construire l’angle dont la tangente = 1 , 220 8°) Construire l’angle dont la cotangente = 0,885

Niveau IV 9°) Le sinus d’un angle 4/5 = 0,800 . Calculer le cosinus et la tangente du même angle. 10°) Le cosinus d’un angle étant 0,550 , trouver ses autres lignes trigonométriques de l’angle. 11°) La tangente de l’angle = 1,6 , déterminer les autres lignes trigonométriques de l’angle. 12°) Le sinus d’un angle est les 3/4 de son cosinus . Trouver les lignes trigonométriques de cette angle et en donner la construction. 13°) On décrit entre les côtés d’un angle AOC un arc AC de 0,90 m de rayon et on trouve 0,60 m pour longueur de la perpendiculaire CP abaissée de C sur OA, quel est le sinus de l’angle ? Calculer ensuite le cosinus et la tangente du même angle. 14°) Montrer que quelque soit l’angle « a » ou a = sin (90° + a ) = cos a .

Travaux : valeurs à donner par le maître :et Calculer les rapports

OP

OP1

OP2

OI

OI1

OI2

PI

PI1

PI2

Calculer les rapports

OP

OP1

OP2

OI

OI1

OI2

PI

PI1

PI2

OP1

OP2

OI

OI1

OI2

PI

PI1

PI2

On, donne : PA = 0A = OP= Calculer : les lignes trigonométries :

Niveau supérieur au niveau V -(BEP) : On vous demande de reprendre les énoncés des exemples et de savoir refaire les exemples : …………….