TAHES : APPLICATIONS.

Pré requis:

Voir :le sommaire des cours sur  " Thalès"

Cours de niveau V .

ENVIRONNEMENT du dossier:

Index        

Objectif précédent  :

Théorème de Thalès  

Objectif suivant :

Niveau BEP propriétés dans le triangle

tableau   

Info sur " Thalès"

 

DOSSIER : THALES : interdisciplinarités

TEST

 

COURS

               

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

                       

 

Corrigé Contrôle 

Corrigé évaluation 

 

Rappel de COURS

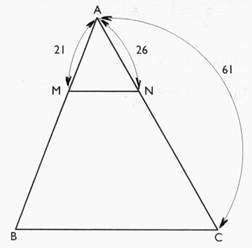
Activité ( suite ):     3 exercices résolus :

1°) Dans un triangle ABC , on donne AM = 21  , AN =  26 et AC = 61 . le segment [ MN ]  est  parallèle  au segment [ BC]  . Calculer la longueur du segment [AB] .

Solution :  d'après la propriété de Thalès on peut écrire :

                 

On remplace les lettres par les valeurs données :

On calcule :

D'où  AB =  49,3

 

 

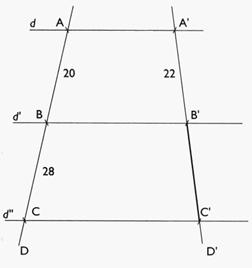
2°) Soit la figure ci -dessous , les droites sécantes D et D' sont coupées par trois parallèles d ; d' ; d" .Sachant que  AB = 20 ; BC = 28 ; A'B' = 22 . Calculer la longueur du segment [B'C']

 

Solution : d'après  Thalès , on peut écrire :

 

Avec  les valeurs données :

 

On en déduit qu'après transformation que : B'C' = 30,8

 

 

 

 

 

 

 

 

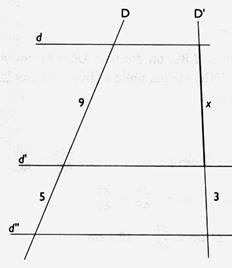
3°) Soit la figure ci - dessous :

calculer "x" :

Solution :      ;    x = 5,4 

 

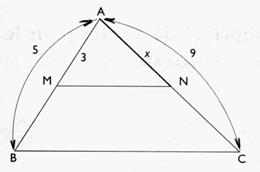
4°) Soit la figure ci - dessous :

 

Calculer  " x "  ;   

  

 

    x = 5,4