|
|
|
|
Les instruments de mesure des angles |
|
|
|
ENVIRONNEMENT du dossier:
|
Objectif précédent |
Objectif suivant : |
DOSSIER : LES PLANS ou FACES perpendiculaires (notions)
|
TEST |
COURS |
Interdisciplinarité |
|
COURS
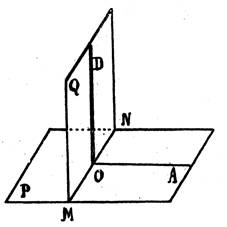
Définition : Un plan « Q » est dit
perpendiculaire à un plan « P » , s’il
contient une droite « delta » ( OD
) orthogonale au plan
« P »
Mais on peut aussi dire que :
Un plan « P » est
dit perpendiculaire à un plan « Q » , s’il
contient une droite « delta » ( OA
) orthogonale au plan « Q »
|
On note : P ^ Q et l’on dit « P est perpendiculaire à Q » |
|
Propriété :
Démontrons que si le plan
« Q » est perpendiculaire au plan « P » ; alors le
plan « P » est perpendiculaire
au plan « Q ».
La droite « delta » de « Q »
orthogonale à « P » au point O
et le plan « Q » coupe le plan « P » suivant une droite
« D » contenant
« O »
Considérons
la droite « D’ » du plan
« P » contenant
« Q » et orthogonale à « D » . La droite «delta » orthogonale
à « P » est orthogonale à la droite « D’ » de
« P ».
Ainsi D’ ^ ![]() et D’ ^ D
et D’ ^ D
La
droite « D’ » orthogonale à deux droites sécantes de « Q »
est donc orthogonale au plan
« Q » .
Le
plan « P » contenant la droite « D’ » orthogonale au plan
« Q » est donc perpendiculaire au plan « Q » .
On
énonce : Si le plan « P »
est perpendiculaire au plan « Q » , alors la
plan « Q » est perpendiculaire
au plan « P » .
Remarque : On pourra
alors dire que les plans « P » et « Q » sont perpendiculaires .
(page 146 )
A savoir :
1°) si deux plans sont perpendiculaires
, toute perpendiculaire à leur intersection incluse dans un des plans est perpendiculaire à
l’autre plan .
2°) Si deux plans sécants sont perpendiculaires à un même troisième , leur intersection est perpendiculaire à ce troisième plan .
|
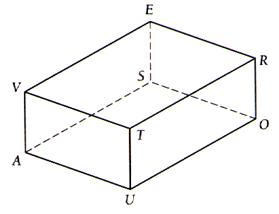
Identifier les
plans perpendiculaires. |
|
|
|
|