WARMATHS

Droites concourantes

Définitions:

Hauteur dans un triangle: voir orthocentre.
Médiane:

dans un triangle: c'est une droite qui passe par un sommet et le milieu du côté opposé.
dans un quadrilatère (polygone à quatre côtés), c'est une droite qui passe par les milieux de deux côtés opposés. Les côtés [AB] et [DC] du quadrilatère ABCD, sont opposés, M et N sont leur milieu respectif. (MN) est l'une des deux médianes de ABCD.

[Quadrilatère]

Médiatrice: c'est une droite qui est perpendiculaire à un segment en son milieu.
Bissectrice: c'est une droite qui partage un angle en deux angles de même mesure.
Diagonale:

dans un polygone (figure qui a plusieurs côtés), c'est une droite qui passe par deux sommets non consécutifs (pas de diagonales dans un triangle: deux côtés quelconques sont consécutifs).
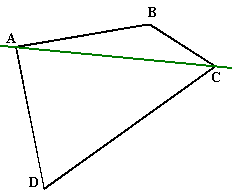
dans un quadrilatère, c'est une droite qui passe par deux sommets opposés. Les sommets A et C du quadrilatère ci-dessous sont opposés. [AC] (notée aussi (AC) comme une droite) est l'une des deux diagonales.

Droites concourantes: ce sont des droites qui ont un point commun. Deux droites non parallèles sont sécantes et sont concourantes au point d'intersection. Lorsqu'il n'y a que deux droites concourantes en un point A, on dit plutôt: "sécantes au point A".

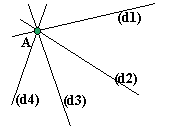
Droites concourantes particulières:

· Dans un triangle:

· les 3 hauteurs sont concourantes en un point appelé orthocentre.

· les trois bissectrices sont concourantes en un point appelé centre du cercle inscrit au triangle.

· les trois médiatrices sont concourantes en un point appelé centre du cercle circonscrit au triangle.

· Les 3 médianes (voir ci-dessous) sont concourantes en un point appelé centre de gravité du triangle.

· Dans un parallélogramme, les diagonales et les médianes sont concourantes en un point appelé centre du parallélogramme. Ce point est un centre de symétrie pour le parallélogramme.

Médianes d'un triangle:

Construction: si, sur notre figure, on connaît le milieu du côté, il suffit de tracer la droite (ou le "morceau" de droite qui nous intéresse) qui passe par ce milieu et par le sommet opposé. Si le milieu n'est pas connu il faut le placer et faire comme précédemment.
Vocabulaire: "médiane relative à un côté" signifie qu'il s'agit de la médiane qui passe par le milieu de ce côté (et par le sommet opposé à ce côté).

[médiane relative93

Propriétés:

Il y a trois médianes dans un triangle (comme il y a trois côtés, trois sommets, trois angles).
Ces trois médianes sont concourantes en un point appelé centre de gravité. Si on connaît deux médianes sécantes en G alors on peut affirmer que la troisième médiane passe par G et coupe le troisième côté en son milieu.

[Troisième médiane]

· BG est le double de GN. CG est le double de GM. Si P est le point d'intersection de (AG) avec [BC] alors AG est le double de GP. Autrement dit: les trois médianes d'un triangle se coupent en un point situé aux 2/3 de chacune d'elles à partir des sommets, et au 1/3 de chacune d'elles à partir des milieux des côtés.

· Si le triangle ABC est équilatéral alors G est aussi centre des cercles inscrit et circonscrit au triangle, ainsi que l'orthocentre. Et seulement dans ce cas.