|
WARMATHS : Collège. |
La Symétrie centrale |
|
|
|
|
|
|
|
|
|
|
|
|
Quadrillage ou
compas. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Une symétrie
centrale de centre O est une transformation qui fait correspondre à tout point A un point B tel que le milieu de [AB] est O.
Le point B est appelé
symétrique de A par rapport à O ou image du point A par la symétrie centrale de
centre O (ce qui est plus long à dire et à écrire...).
Si le symétrique
de A par rapport à O est B
Alors O est le
milieu du segment [AB].
et:
Si O est le
milieu du segment [AB]
Alors les points
A et B sont symétriques l'un de l'autre.
3°) Construction du
symétrique d'un point:
Soit le
point O centre d'une symétrie. Tracer le symétrique par rapport à O d'un point
A donné.
Deux
techniques peuvent être utilisées:
a)
par comptage des carreaux de la feuille:
|
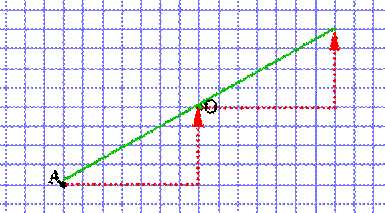
Le point A et le
point O sont déjà placés sur votre feuille. En
suivant la ligne en pointillés rouges: - Comptez
horizontalement le nombre de carreaux qui séparent A et O (7 vers la droite sur
la figure ci-contre). Puis faites de même
mais verticalement (4 vers le haut sur la figure). - A partir de O
faites la même chose et dans le même ordre: 7 carreaux vers la droite puis 4
carreaux vers le haut. Le point trouvé est
le symétrique de A par rapport à O et O est le milieu de [AB]. |
|
Dans le
cas d'une feuille non quadrillée ou lorsque les points donnés ne se trouvent
pas sur des noeuds du quadrillage, appliquez la seconde méthode ci-dessous.
b)
à l'aide des instruments de dessin:
Les
figures ci-dessous donnent la procédure à suivre pour construire le symétrique
A' du point A par rapport au point O:
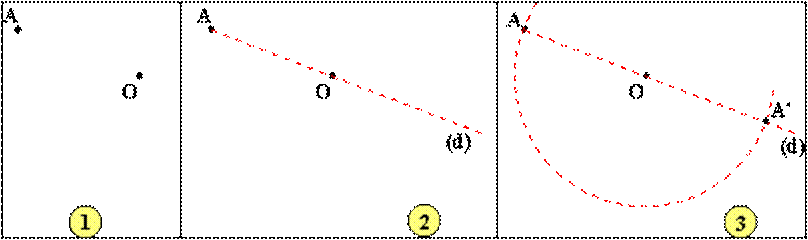
1. Données: le
centre de symétrie O et le point A.
2. Tracez la droite
(d) passant par A et O. Prolongez la au delà de O.
3. Avec un compas
pointé en O et un écartement égal à OA, recoupez (d) en A'.
4°) Symétriques de quelques figures
simples:
Les figures
ci-dessous sont construites avec le point O pour centre de symétrie.
Les lignes rouges en
pointillés sont des lignes de construction.
Les petites croix
rouges indiquent que O est milieu d'un segment.
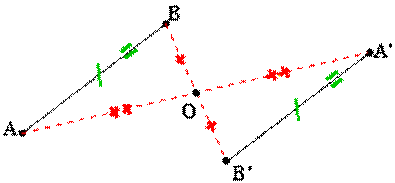
Pour construire le
symétrique d'un segment [AB] nous construisons les symétriques de ses points
extrémités A et B.
|
Le symétrique du
segment [AB] par rapport à O est un segment: -
de même longueur. -
parallèle au segment [AB]. |
|
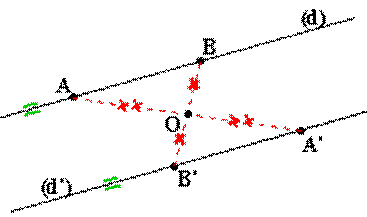
Pour construire le
symétrique d'une droite (d) nous construisons les symétriques de deux de ses
points A et B choisis à notre convenance.
|
Le symétrique d'une
droite (d) par rapport à O est une droite (d') parallèle à (d). |
|
Pour construire le
symétrique d'un angle nous choisissons un point sur chacun de ses côtés et nous
en construisons le symétrique ainsi que le symétrique de son sommet.
|
Le symétrique d'un
angle est un angle: -
de même mesure -
dont les côtés sont parallèles aux côtés de l'angle donné. |
|
|
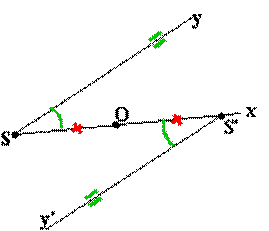
Un cas particulier
intéressant est lorsque le centre de symétrie O se trouve sur l'un des côtés
de l'angle. |
|
|
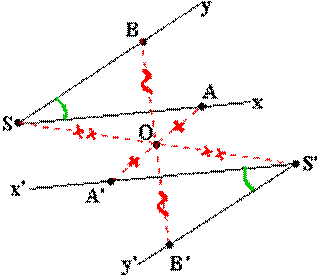
Par exemple, sur la
figure ci-contre nous avons le centre de symétrie O sur le côté [Sx): -
S', le symétrique de S, se trouve sur [Sx). -
[Sy) et son symétrique [S'y')sont
parallèles. Nous avons donc une
bande à bords
parallèles (Sy) et (S'y') coupée par une sécante
(SS'). Les angles alternes internes marqués en vert sont égaux. |
|
d)
symétriques de deux droites parallèles:
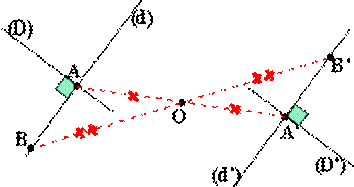
Pour construire les
symétriques de deux droites parallèles (D) et (d) il suffit de choisir sur
chacune d'elle un point (A sur (D) et B sur (d) par exemple) et d'en construire
leur symétrique (A' et B' par exemple).
Ensuite vous tracez les droites
parallèles à (D) et (d) et passant par A' et B'.
|
Les symétriques de
deux droites parallèles (D) et (d) sont deux droites parallèles (D') et (d').
De plus les deux
droites (D) et (d) et leurs symétriques sont parallèles. |
|
Remarque: pour
simplifier la construction vous pouvez choisir un point A sur (D) et comme
point sur (d), le point d'intersection de (OA) avec (d) (représenté sur la
figure ci-dessus par C en gris).
e)
symétriques de deux droites perpendiculaires:
Pour construire les
symétriques de deux droites perpendiculaires (D) et (d) sécantes en A, le plus
simple est:
- construire A'
le symétrique de A.
- choisir un
point B sur l'une des droites données (sur (d) par exemple) et en construire le
symétrique B'.
- tracer (A'B') qui est la droite symétrique
de (d).
- tracer en A' la
droite perpendiculaire à (A'B').
|
Les symétriques de
deux droites perpendiculaires (D) et (d) sont deux droites perpendiculaires. Bien sûr (D) et (d)
sont aussi parallèles à leur droite symétrique respective (c'est à dire (D)
parallèle à (D') et (d) parallèle à (d') ). |
|
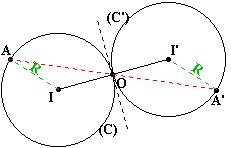
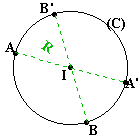
Pour construire le
symétrique d'un cercle de centre I et de rayon connu R, vous devez procéder
dans l'ordre:
- construire le
symétrique du centre I du cercle donné. Soit I' ce symétrique.
- tracer un
cercle de centre I' et de rayon R.
|
Le symétrique d'un
cercle de centre I et de rayon R est un cercle: -
de même rayon. -
dont le centre est le point I' symétrique de I.. |
|
Remarques:
dans le cas de figure ci-dessus,
le centre de symétrie O est placé à l'extérieur du cercle de centre I et de
rayon R. D'autres cas de figures intéressants à étudier peuvent se présenter:
|
Le
centre de symétrie O est sur le cercle: O est
donc milieu de [II'] ( IO=OI'=R). Les deux cercles sont donc tangents extérieurement. La
droite tracée en pointillés noirs est une tangente commune aux deux cercles
(elle est perpendiculaire à (II') droite des
centres). |
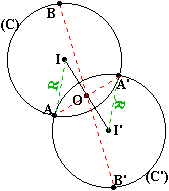
Le
centre de symétrie O est à l'intérieur du cercle sans être en son centre: Le
cercle de centre I et de rayon R et son cercle symétrique sont sécants. Ils se coupent en deux
points A et A'. Ces deux points d'intersection sont symétriques l'un de
l'autre par rapport à O. (AA')
est la sécante commune aux deux cercles. Elle est perpendiculaire à la droite
des centres (II'). |
Le
centre de symétrie O est au centre I du cercle: Dans ce
cas (le plus simple) tout point du cercle est symétrique du point
diamétralement opposé (c'est à dire qu'un point donné et son symétrique
forment les extrémités d'un diamètre). Le
cercle se transforme en lui-même. |
|
|
|
|
5°) Propriétés conservées par symétrie
centrale:
Le paragraphe
précédent illustre les propriétés suivantes:
Les symétries
centrales conservent:
Les distances.
Le parallélisme et l'orthogonalité.
Les mesures des angles et les
alignements.
Les aires: le calcul sur les aires utilise des
longueurs et des propriétés (angles notamment) qui sont conservées.
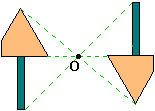
6°) Figures possédant un centre de
symétrie:
Une figure
possède un centre de symétrie lorsque le symétrique de cette figure par rapport
à ce centre, est la figure elle-même. Autrement dit: la figure se transforme en
elle-même.
Exemples:

Tous les parallélogrammes (avec
leurs cas particuliers: losanges, rectangles et carrés) ont pour centre de
symétrie, le point d'intersection de leurs diagonales.
L'hexagone (six côtés
égaux, six angles égaux) est un polygone
qui admet l'intersection de ses diagonales comme centre de symétrie.
Le cercle admet son
centre comme centre de symétrie (voir dans ce document).