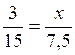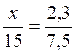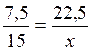tableau : SOMMAIRE »
>>>>Devoir auto formatif	>>>> Devoir formatif	>>>>-Cours 1   et >>>>>cours 3 -
		>>>>  CORRIGE
Devoir   :   COURS 2 / 3 sur   LES GRANDEURS PROPORTIONNELLES.

Ce cours prépare celui sur la fonction linéaire.  Ce  cour est en 3 parties :

 

COURS PARTIE  2 :

 

Recherche de la   4^ème proportionnelle

CONTROLE :

 

 

1- Lorsque l’on a  une égalité de deux fractions :  (dans une proportion) et si  l’on connaît 3 valeurs sur 4 , on peut trouver la « quatrième » valeur .

On dira «  rechercher la quatrième proportionnelle. »

 

2- Les  cas rencontrés sont 

 

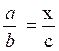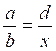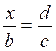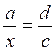               ;       ;                ;                  ;    autre cas :  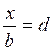  ou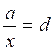  

 

3- Dans une proportion,  (égalité de deux fractions)  le produit des extrêmes est égal aux produits des moyens.

 

4 - Traduction mathématique :        si   =   alors ad = cb

 

nota : lorsque le produit est « écrit »  , on doit « résoudre l’équation » pour trouver la quatrième valeur manquante.

 

5-   Calcule de  « x » dans chacun des  cas suivants :

 

	3 fois 7,5 = 15  fois « x »	X = 1,5
	x = 2,3 fois 15 : 7,5 =	X = 4,6
	7,5 fois « x » =  15 fois 22,5	X = 45

 

Ces calculs vont permettre de compléter les tableaux de    proportionnalités.

 

Interdisciplinarité : travaux repris en sciences. Des connaissances en sciences sont nécessaires pour comprendre le travail demandé ;   (à vous de vous informer)

1°) Calculer la mesure de la d.d.p. aux bornes d’un résistor dans les cas suivants :

 

calibre	Echelle	lecture	corrigé
3 V	[ 0 ; 30 [	22 divisions	=  ;           x =  22,1 V

2°) Quelle est l’intensité du courant traversant le circuit ?

Calibre	Echelle	lecture
0,1 A	( 0 ; 100)	57 divisions =   =  ;      x = 0,057  A ou 57mA

3°)  Une voiture consomme 18,4 L d’essence pour effectuer le trajet Paris - Caen  ( 230 km) .Quelle sera sa consommation pour effectuer le trajet  Paris  - Cherbourg  long de 340 km ?

Que devons nous admettre pour résoudre le problème ?

On pose:        =  ;	x = 27,2 l
Conclusion: Nous considérons que la consommation est constante	La consommation pour 340 km parcourus sera de 27,2 litres

4 °) La masse et le volume d’un corps sont deux grandeurs directement proportionnelles .Le coefficient de proportionnalité s’appelle la « masse volumique » du corps.

 

a)   Calculer le volume d’un corps de masse  52 kg dont la masse volumique est  de 23 kg /dm³

b)    

On pose :  =  ;     =  ;	Calcul: 52 fois 1 :23
Volume = 2,2608696 dm3

 

Complément de cours (partie 2 )  :

1 )  De l’égalité 3,4 x 7,8  =  2,4 x 11,05 ; déduire toutes les proportions possibles.

 

On sait que 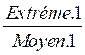 est égale à 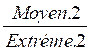      si     

           

               Extréme.1  "fois"   Extréme.2  =  Moyen .2  "fois"  Moyen.1 ;

 

a)  On remplace  :  3,4  "fois"  7,8  =  2,4  "fois"  11,05

b) on remplace  dans :

                                est égale à  

On sait que : Dans une proportion, on peut permuter les « extrêmes »«  ( l’égalité reste vraie)

traduction mathématique

si   =   alors    =     ;             si  =  alors si  =

 

Dans une proportion, on peut permuter les « moyens » ,(l’égalité reste vraie)

traduction mathématique

 

si   =   alors    =   _;          donc  :     si  =   alors si  =  ou  =

Solutions

=

=

=

=