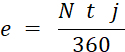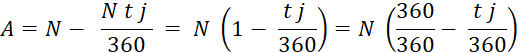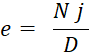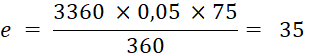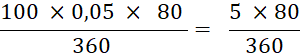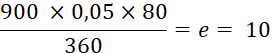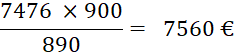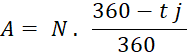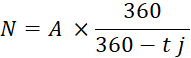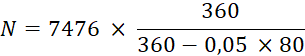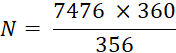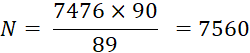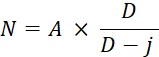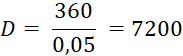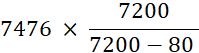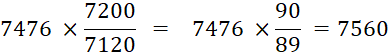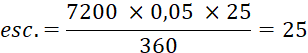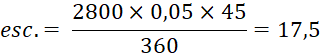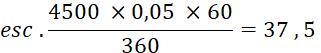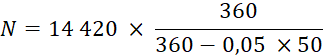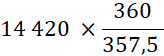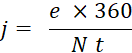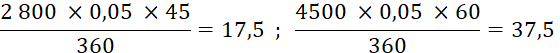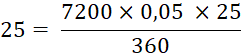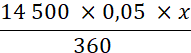Dans les exercices :  Remplacer les unités « francs » par les « euros »

L’escompte : Le propriétaire d’un effet de commerce peut avoir besoin d’argent immédiatement. Il porte son effet à une banque qui lui paie la valeur nominale diminuée d’une certaine somme appelée l’escompte. On dit que l’effet a été escompté.

La banque qui a escompté un effet, en devient propriétaire et se fait rembourser par l’acheteur le jour de l’échéance.

L’escompte est égal à l’intérêt de la valeur nominale compté du jour où l’effet a été escompté jusqu’au jour de l’échéance.

Dans le calcul du temps, on compte le jour où l’effet a été escompté, on ne compte pas le jour de l’échéance, et on compte exactement le nombre de jours entre ces deux dates. Toutefois, pour simplifier, l’année est toujours supposée égale à 360 jours.

Les calculs relatifs à l’escompte sont analogues aux calculs d’intérêt simple ; une seule différence : l’escompte se retranche de la valeur nominale alors que l’intérêt s’ajoute au capital. On donne le nom de valeur actuelle d’un effet à la somme payée par le banquier. En résumé :

Escompte = Intérêt de la valeur nominale.

Valeur actuelle = Valeur nominale – Escompte.

Formules de l’escompte

Elles se déduisent de celles de l’intérêt.

Si l’effet de commerce de valeur nominale N est escompté pour « j »  jours au  taux de « t % », l’escompte « e »    est donné par t formule

Si « t » est la valeur décimale  du calcul  du a% 

Par exemple : a %   vaut  3 % =  = alors  t = 0,03

Dans la formule de « e »  la valeur de  « t » est un nombre décimal qui est  égal à « a »  divisée par « 100 ».

Calcul de la valeur actuelle : ( A )

Soit « A »  la valeur actuelle de l’effet .

La valeur actuelle « A »    de l’effet est donc

)

Donc

Remarques :

Soit 

1°) Si on utilise la méthode des nombres et diviseurs pour le calcul de l’escompte, le diviseur D est égal à  

L’égalité   

Les formulent ci-dessus se simplifient et deviennent

1.    2 - En plus de l’escompte, les banques retiennent divers autres frais accessoires (droit de commission, droit de change de place, taxe sur le chiffre d’affaires,...). Ces droits s’évaluent en tant pour cent de la valeur nominale, où  ils ont une valeur fixe. L’ensemble de ces frais et de l’escompte constitue l’Agio.

Dans les problèmes d’escompte, on ne tient pas généralement compte des frais.

Problèmes sur l’escompte

Ils sont semblables à ceux étudiés à propos de l’intérêt. On a cinq grandeurs : valeur nominale de l’effet, taux de l’escompte, temps (en jours), escompte, valeur actuelle.

Connaissant trois de ces grandeurs, on peut déterminer les deux autres, grâce aux relations ci-dessus.

1^er exemple. Calcul de l’escompte et de la valeur actuelle.

                            On escompte le 16 juin une traite de 3 360 euros payable le 30 août. Calculer la valeur actuelle de la traite le taux de l’escompte étant de 5 %.

                               Calcul du nombre de jours :

    Du 16 juin au 30 août il y a 15 jours en juin, 31 en juillet et 29 en août (compter le 16 juin, ne pas compter le 30 août), soit au total :

15 + 31 + 29 = 75 jours

Calcul de « e » :                  on sait que   (  )

L’escompte (intérêt de 3 360 €  en 75 jours) à 5 % est donc  ( attention t = 0,05 )

Calcul de « A »   :                   

La valeur actuelle de la traite est donc

A = 3 360 – 35 = 3 325 €

2^ème exemple. Calcul de la valeur nominale connaissant la valeur actuelle.

Calculer la valeur nominale d’une traite payable dans 80 jours, escomptée à 5 % pour laquelle le banquier a payé 7 476 € .

( A = 7476 )

Solution arithmétique : on détermine la valeur actuelle d’une traite de valeur nominale donnée dans les conditions indiquées, et on en déduit la valeur nominale demandée.

L’escompte d’une traite de 100 €   à 5 % pour 80 jours serait

ou encore, l’escompte d’une traite de 900 €  serait de 10 €  et sa valeur actuelle.

Valeur actuelle :                      900 – 10 = 890 €

La valeur nominale de la traite est donc  les   de la valeur actuelle soit :

Emploi des formules

D’où

( par transformation de l’égalité ci-dessus)

Attention «  t = a/100)

«  t = 5% =  0,05 »

Calcul rapide

On sait que   

( A = 7476 )

Rappel :

Négociation des effets de commerce

Les effets de commerce peuvent être vendus ou échangés. Leur valeur est égale à leur valeur actuelle le jour de la négociation.

Echéance commune

Ce problème consiste à remplacer plusieurs effets par un effet unique venant à échéance à une date donnée. Il faut déterminer la valeur nominale de cet effet.

Exemple.

Une personne doit régler à un fournisseur trois traites : la 1^ère de 7 200 €  payable le 5 avril ; la 2^ème de 2 800 €  payable le 25 avril ; la 3^ème de 4 500 €  payable le 10 mai.

Le 10 mars elle demande à ce fournisseur de remplacer ces trois traites par un effet unique payable le 30 avril.

Quelle doit être la valeur nominale de cette traite unique ?                 Taux d’escompte : 5 %  ( soit : t = 0,05)

1^er effet à échéance : 25 j.

2^ème effet à échéance : 45 j.

 .      

3^ème effet à échéance : 60 j.

On a donc à trouver la valeur nominale d’un effet de valeur actuelle 14 420 €  payable dans 50 jours.

Échéance moyenne

Ce problème consiste à remplacer plusieurs effets par un effet unique ayant pour valeur nominale la somme des valeurs nominales. Il faut déterminer la date d’échéance de ce billet unique.

Exemple

On remplace les trois traites de l’exercice précédent par une traite unique de valeur nominale 7 200 + 2 800 + 4 500 = 14 500 € . Quelle est la date de l’échéance ?

La valeur actuelle de ce billet unique est égale à la somme des valeurs actuelles des trois billets, ou encore l’escompte de cette traite unique est égale à la somme des escomptes des trois traites soit 25 + 17,5 + 37,5 = 80 € .

On a donc à trouver la date de l’échéance, connaissant la valeur nominale 14 500 €  de la traite unique et son escompte 80€  au taux de 5 %.

La date de l’échéance sera donc le 20 avril.

Remarque :

En remarquant que

La somme des 3 calculs est égale à 80 € .

Et que l’escompte du billet unique est, en appelant  la durée de l’échéance à déterminer ;

Ou

On a donc       :

On a donc : 

Donc : 

En remarquant que le produit de la valeur nominale par le temps, représente le nombre de ce capital, on voit que l’échéance moyenne s’obtient en divisant la somme des nombres par la somme des valeurs nominales.

Compensation. Une banque d’une ville peut céder à une banque d’une autre ville les effets payables dans cette dernière, et réciproquement.

Exemple.

Une banque de Toulouse cède à une banque de Paris les effets payables à Paris et reçoit de la banque de Paris les effets payables à Toulouse. Pour établir le compte de cette opération, on détermine les valeurs actuelles des billets échangés et on calcule la différence.

Cette opération s’effectue également avec les banques de pays étrangers, pour le commerce extérieur.

TRAVAUX AUTO FORMATIFS.

CONTROLE

Compléter  les phrases suivantes :

Dans le commerce, les paiements importants se font rarement au comptant, mais le plus souvent à terme, c’est-à-dire à une date fixée après la livraison de la marchandise. Dans ce cas, au moment de la livraison, l’acheteur signe un engagement sur papier timbré, appelé « effet de commerce ».

C’est toujours le vendeur qui conserve l’effet de commerce, afin de pouvoir se faire payer par l’acheteur à la date indiquée.

La somme portée sur l’effet est sa valeur nominale, et la date prévue pour le paiement est l’échéance. Il y a deux sortes d’effet de commerce 

EVALUATION :

Faire les EXERCICES  suivants :

1)   Quelle est la valeur actuelle d’un billet de 2 700 euros, escompté à 6 % et payable dans 90 jours ?

2)   Calculer à 5 ½ %, l’escompte d’un billet de 4 800 € , payable le 15 juin et présenté à la banque le 16 avril précédent.

3)   Quelle somme un banquier donnera-t-il pour un billet de 1 440 €  payable dans 90 jours et escompté à 5 % ?

4)   Un commerçant a vendu à un acheteur 24 mètres de drap à 32 €  le mètre et 36 mètres de soie à 22 euros, le tout payable dans 90 jours, par traite acceptée. Calculer la valeur de la traite le jour de la livraison de l’étoffe. Taux 5 %.

5)   Un négociant porte à la banque 3 traites, l’une de 4 800 francs payable dans 45 jours, l’autre de 7 200 euros payable dans 30 jours et la troisième de 8 000 euros payable dans 36 jours. Le taux de l’escompte étant 6 %, quelle somme touchera-t-il ?

6)   Une personne présente chez un banquier le 15 septembre une traite de 360 euros payable le 30 octobre et une traite de 630 euros payable le 14 décembre. Le banquier escompte les deux traites au taux de 5 %. Quelle somme remet-il à la personne ?

7)   Un banquier a retenu 81,9 €  d’escompte sur un billet de 5 460 euros payable dans 90 jours. Quel a été le taux de l’escompte ?

8)   Le 5 mai, on a présenté une traite de 8 640 euros, payable le 19 juin, à un banquier qui a remis une somme de 8 596,8 €  Calculer le taux de l’escompte.

9)   On escompte chez un banquier deux effets de commerce, l’un de 4 800 € payable dans 72 jours, l’autre 5 000 €  payable dans 90 jours. On reçoit 182,60 €  de plus pour le second que pour le premier. Quel est le taux de l’escompte ?

10)         Deux traites, l’une de 800 €  payable dans 108 jours, l’autre de 600 €  payable dans 112 jours sont escomptées en même temps. On reçoit 1 374,4 € . Calculer le taux de l’escompte.

11)         Pour un billet de 300 € , escompté à 5 % un banquier a payé 297 € . Dans combien de temps ce billet était-il payable ?

12)         Un banquier escompte le 13 août une traite de 500 F à 5 ½ %, et remet la somme de 491,75 F. Calculer la date de l’échéance de la traite.

13)         Une traite de 1 500 F, escomptée à 5 % a été payée 1 481,25 F. Dans combien de jours aura lieur l’échéance ?

14)         Une personne fait escompter le 3 mars deux effets de commerce. L’un de 800 € , l’autre de 1 600 € . Elle reçoit 2 368 €. Le taux de l’escompte est 6 %. Sachant que le premier effet était payable le 2 mai, calculer la date de l’échéance de l’autre.

15)         Quelle est la valeur nominale d’un billet payable dans 60 jours, escompté à 6 % sachant que sa valeur actuelle est de 2 475 €  ?

16)         On fait escompter à 6 % le 1^er avril une traite payable le 21 mai suivant. Quel était le montant de cette traite sachant qu’elle a subi un escompte de 52,5 €  ?

17)         Une facture payable dans 90 jours a été payée au comptant 788 € . Sachant qu’on l’a diminuée de l’escompte à 6 %, quel était le montant de la facture ?

18)         Un billet payable dans 45 jours est escompté au taux de 5 %. Sa valeur actuelle est de 2 703 € . Quelle est la valeur nominale de ce billet ?

19)         Une traite payable dans 80 jours, escomptée à 6 % donne lieu à un escompte de 49,6 € . Quel était le montant de cette traite ?

20)         Le 30 mars, un banquier a retenu 10,8 €  sur une traite payable le 23 mai. Calculer la valeur nominale de la traite sachant que le taux de l’escompte est 4,5 %.

21)         On remplace deux effets de commerce : l’un de 3 600 €  payable dans 108 jours, l’autre de 2 700 €  payable dans 112 jours, par un billet unique de même valeur actuelle que les deux billets précédents et payable dans 160 jours. L’escompte étant de 5 %. Calculer la valeur nominale de ce nouveau billet.

22)         Un commerçant a souscrit trois effets : le premier de 720 €  payable dans 30 jours ; le deuxième de 540 € payable dans 45 jours, le troisième de 360 €  payable dans 60 jours. Il propose de les remplacer par un billet unique payable dans 90 jours. Le taux de l’escompte étant de 5 %, quelle doit être la valeur nominale de ce billet unique ?

23)         Un commerçant a souscrit trois effets : le premier de 8 000 €  payable dans 30 jours, le deuxième de 3 200 €  payable dans 75 jours, le troisième de 4 800 €  payable dans 120 jours. Elle propose de les remplacer par un billet unique ayant pour valeur nominale la somme des valeurs nominales soit 16 000 € . Quelle doit être l’échéance de ce billet unique ?

24)         Une banque de ville A adresse le 12 avril à une banque de la ville B les effets suivants :

Et reçoit de cette même banque les effets suivants :

Établir le compte de compensation entre les deux banques. (Le taux de l’escompte est 6 %).