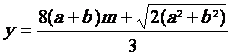Multiplicande 

5 a³

- 7 a²b 

+ 3ab²

+  4b³  

Multiplicateur

3a²

— 8 ab  

— b²   

Total :

1°) . Quel est le produit de14a³b²c par 9abdm ?

=  126 a ⁴ b³ c d m

2°) Multiplier :  - ¾  mn  par 36 mx

- 27 m²nx

3°) Effectuer le produit de 8 ab³ y par — 7 a² cx

8 a ³ b³ y cx

4°) Faire le produit de – 5 a b² x² par – 12 amx

+ 60  a²  b² m x³

5°) Trouver le produit des trois facteurs  5 a b  ( - 3 b c ) (  + 7 ad)

(- 15 a b² c ) ( + 7 ad) =  - 105 a² b² c d

6°)  Effectuer l’opération :

( 13 ab ) ( - a²) =  ( - 13 a ³ b )

+ 7 a² ( a b) =   7 a ³ b

( 8 a – 3 b + 5 c ) 7 a =  56 a²  - 32 ab + 35 ac

2a ( a ³ – 5 a²b + 3 a b² - b³ ) =  2 a ⁴ – 10 a³ b + 6 a² b² - 2a b³

B

( a² -1 ) ( a ⁴ – a²b + b² ) =

( 3 a² - 5 a ² b – ½ a b ² ) ( - 2 a² + 3ab – b²) =

a b ( a⁵ + a ⁴ b + a ³ b² + a² b³ + a b ⁴ + b ⁵ )  = 

( 3 x² - 5 x + 7 ) ( x +4)   +  ( 2 x² - 8 x + 3 ) ( x – 4 ) =

( 2 x² + ax – a² )  (x² + 2 ax a²) –  ( x²  + 3 ax – 2 a² ) ( x² - a²) =  

Calculs :

1° ) On demande de calculer la valeur de v dans la formule v = (R² +  r² + R r )  sachant que

 = 3,1416, R  = 4,   r = 3,  H  = 1,5. (Rép. V  = 58,12.)

2°)  Dans l’expression x = b ( a + b) ( b+c) – ( a² - b²)  quelle serait la valeur de x pour a= 8 ; b = 5 ; c = 4  ( rep. X = 390 )

3°) Que devient :  quand on suppose a = 10 ; b = 7 et m = 2   ( rép : 136,69 )

4°) Décomposer en deux facteur le trinôme a²x + bx – cx

5°) Séparer les facteurs communs aux termes du polynôme : 7 a³x – 7 a² x² + 7 a x³

6°)   Décomposer a ³ — a²    en deux facteurs

7°)  Mettre en facteurs communs l'expression 9 a b ³  + 15 a² b² - 24 b²

8°) Quel est le produit de a ^m  par aⁿ ?

9°) On demande la racine carrée suivante : x² + 2 bx + b²   .. ( x + b) ²   ; racine =  x=b

10°)  Quelle est la racine carrée de x ²  — 6x +  9 ?

11 °) Les deux premiers termes du carré d'un binôme sont x ² + 10 x ;  quel est le  troisième ?

12 °) Étant donnés les deux termes x ² - 7x  , com­pléter le trinôme pour que ce soit un carré parlait.

13 °)  Décomposer x ²  — y ²  en deux facteurs binô­mes.

14°) Quels sont les deux facteurs binômes numériques qui ont donné le produit 100 — 16 ?

15°)  Transformer l'expression  R =    en  une expression équivalente.  Rep = 

16°) Trouver la différence qui existe entre le carré de  a et le carré de a +1   Rep = 2a + 1

17 °) Appliquer  la propriété du problème précédent aux carrés de 37 et de 38.  REp :  37 et   37+1 ;  =   75

18° )  Faire le cube du binôme a + b  et, de  sa com­position, déduire une loi générale pour former le cube de la somme de deux quantités quelconques

19°) Trouver la différence de « a » au cube de a + 1.

20 ° )Appliquer le problème précédent aux cubes de  37 et de 38.